代码随想录Day22——回溯1

回溯可解决的问题：

1. 确定参数
2. 确定终止条件 path.size==k
3. 确定单层循环

递 推 小 结：
1、递推是从已知条件开始；
2、递推必须有明确的通用公式；
3、递推必须是有限次运算。
递 归 小 结：
1.递归：未知的推到已知的，再由此返回。
2. 基本思想：将复杂的操作分解为若干重复的简单操作。

77 组合

需要一个二维数组记录结果，一个一维数组记录路径

注意带***的

class Solution {
    List<List<Integer>> result=new ArrayList<>();
    LinkedList<Integer> path=new LinkedList<>();
    public List<List<Integer>> combine(int n, int k) {
        backtracking(n,k,1);
        return result;
    }
    public void backtracking(int n,int k,int index){
        if(path.size()==k){
            result.add(new ArrayList<>(path));//***
            return;
        }
        for(int i=index;i<=n;i++){
            path.add(i);
            backtracking(n,k,i+1);
            path.removeLast();//***
        }
    }
}

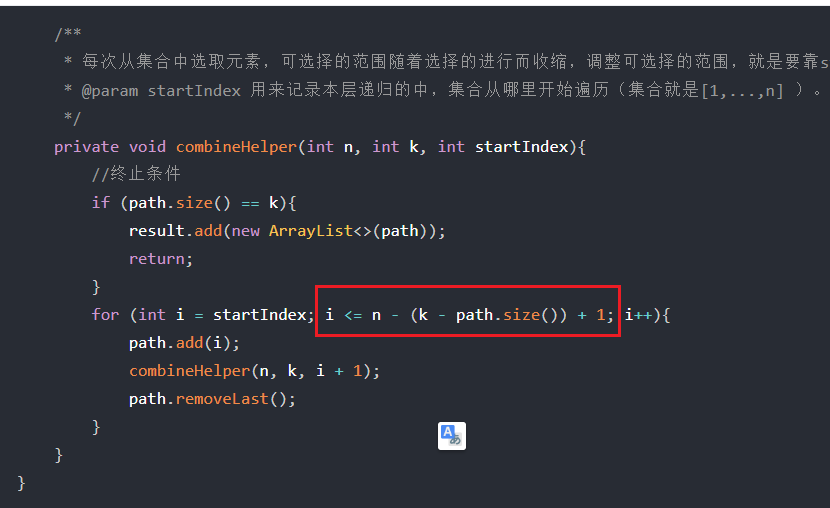
剪枝优化

216 组合综合III

注意sum的回溯，未剪枝优化版本

class Solution {
    List<List<Integer>> result = new ArrayList<>();
    LinkedList<Integer> path =new LinkedList<>();
    public List<List<Integer>> combinationSum3(int k, int n) {
        backTracking(n,k,1,0);
        return result;
    }

    public void backTracking(int n,int k, int index,int sum){
        if (path.size() == k) {
			if (sum == n) result.add(new ArrayList<>(path));
			return;
		}
		for (int i = index; i <= 9 ; i++) {
			path.add(i);
			sum += i;
			backTracking(n, k, i + 1, sum);
			//回溯
			path.removeLast();
			sum -= i;
		}
    }
}

17 电话号码的字母组合

class Solution {
    List<String> result = new ArrayList<>();

    public List<String> letterCombinations(String digits) {
        if(digits==null ||digits.length()==0) return result;
        String[] list={"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
        backTracking(digits,list,0);
        return result;
    }

    // 每次迭代获取一个字符串，所以会涉及大量的字符串拼接，所以这里选择更为高效的 StringBuilder
    StringBuilder temp = new StringBuilder();

    public void backTracking(String digits, String[] list, int num) {
        //遍历全部一次记录一次得到的字符串
        if (num == digits.length()) {
            result.add(temp.toString());
            return;
        }
        //str 表示当前num对应的字符串
        String str = list[digits.charAt(num) - '0'];
        for (int i = 0; i < str.length(); i++) {
            temp.append(str.charAt(i));
            //递归，处理下一层
            backTracking(digits, list, num + 1);
            //剔除末尾的继续尝试
            temp.deleteCharAt(temp.length() - 1);
        }
    }
}