关于加减运算时能否使用等价无穷小的问题

众所周知，任意一个非无穷小，也非无穷大的数，加减一个无穷小的数，结果都为自身：

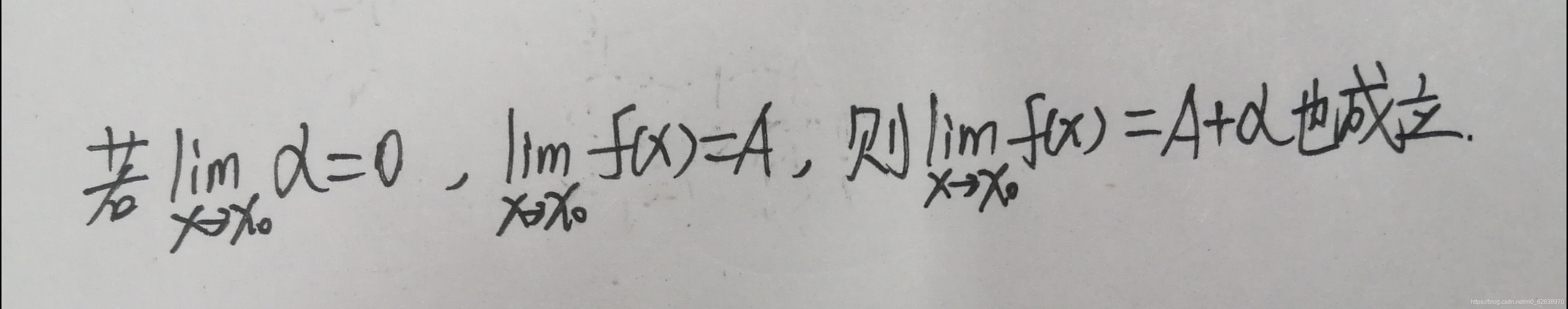
又众所周知，高阶无穷小与低阶无穷小的比值为0，0也为特殊的无穷小：
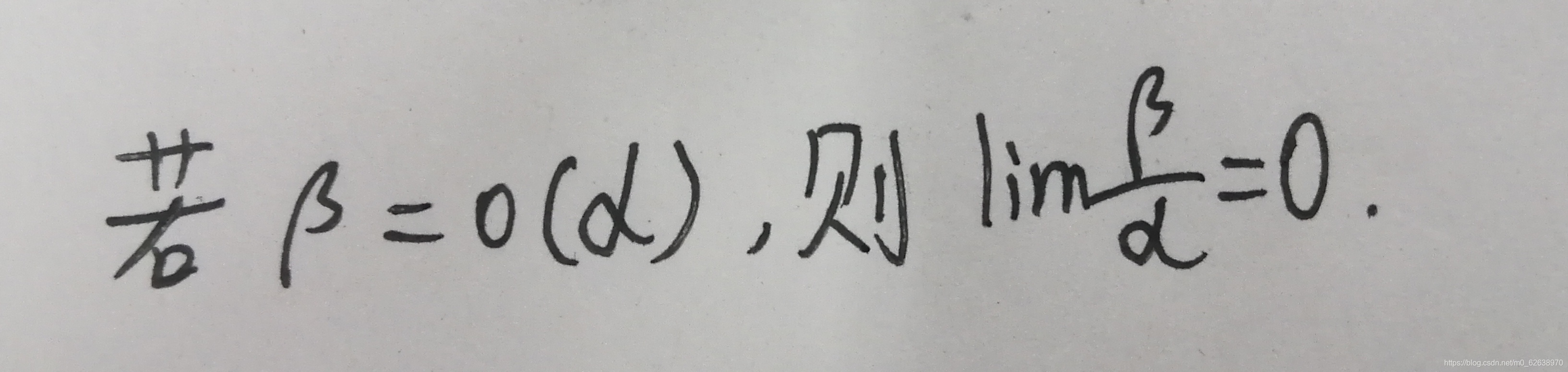由此我们可得知如下公式：

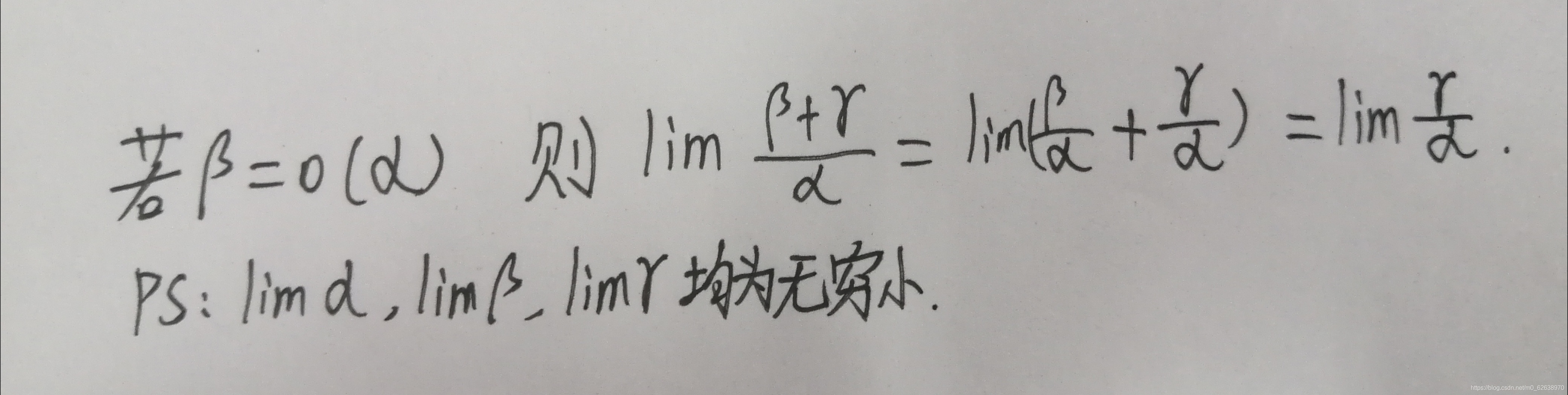
由此我们就可以粗略判断出在加减运算时是否可以直接利用等价无穷小了。
事实上，同理同阶无穷小也是可以用这个方法提出来的。
比如说举个例子：

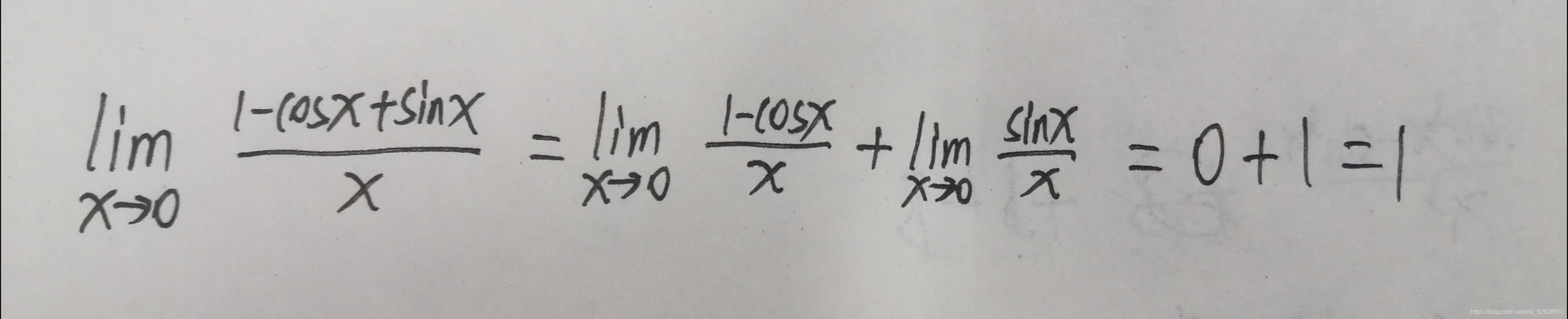
这也能解释我们最初遇到的典型反例为什么不能用等价无穷小运算了，因为tanx或者sinx都不是x三次方的高价无穷小，都不能随意提出来：

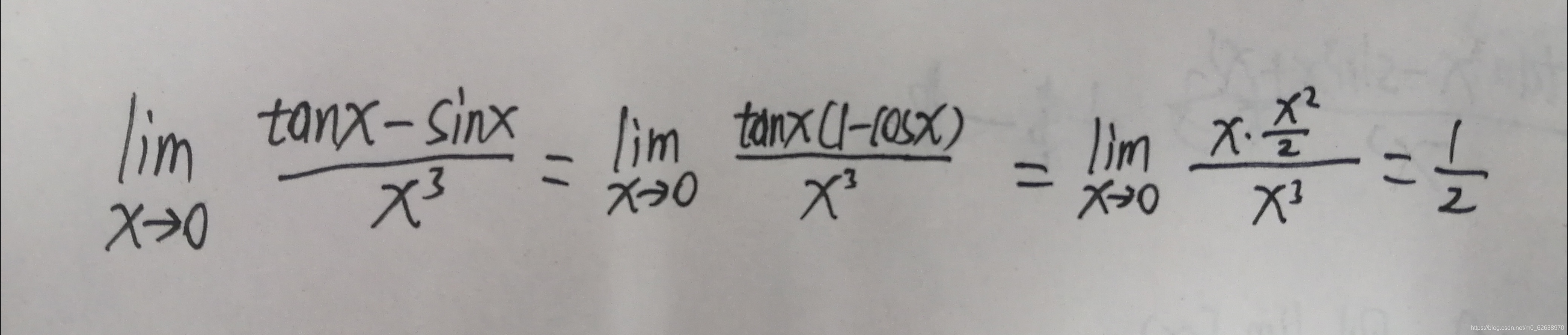
以上均为个人猜想，所以如果有错误还请及时指出。
谢谢您的观看。