【英文文章翻译】(Wei Zhu,2019)A first-order image denoising model for staircase reduction（用于阶梯降噪的一阶图像去噪模型）

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

---

前言

本篇博客是对**(Wei Zhu,2019)A first-order image denoising model for staircase reduction**（用于阶梯降噪的一阶图像去噪模型）的翻译文本，直接从word文档中粘贴出来，因为粘贴不了文档中的公式，有许多内存丢失了，如果需要word原文（包含公式）请私信。

摘要：在本文中，我们考虑了一种基于变分法的图像去噪模型，该模型能够缓解Rudin-Osher-Fatemi模型所具有的众所周知的阶梯现象（Rudinetal.,Phys.D60,259–268,1992）。为了最小化这种变分模型，我们采用了增强拉格朗日方法（ALM）。对所提出的算法进行了收敛性分析。数值实验证明了所提出模型的特征，并且也展示了所提出数值方法的效率。

关键词：图像去噪；增强拉格朗日方法；变分模型

Afirst-orderimagedenoisingmodelforstaircasereduction

Abstract：Inthispaper,weconsideratotalvariation–basedimagedenoisingmodelthatisabletoalleviatethewell-knownstaircasingphenomenonpossessedbytheRudin-Osher-Fatemimodel(Rudinetal.,Phys.D60,259–268,1992).Tominimizethisvariationalmodel,weemployaugmentedLagrangianmethod(ALM).Convergenceanalysisisestablishedfortheproposedalgorithm.Numericalexperimentsarepresentedtodemonstratethefeaturesoftheproposedmodelandalsoshowtheefficiencyoftheproposednumericalmethod.
Keywords：Imagedenoising；AugmentedLagrangianmethod；Variationalmodel

1 引言

图像去噪的目的是去除给定图像中的噪声部分，以得到一个干净的图像，并在其中大部分保留有意义的信号。这是一个典型的逆问题，为了解决这样的问题，通常应该采用适当的正则化器。在文献中，Rudin、Osher和Fatemi(ROF)[30]给出了该问题最著名的变分模型之一，其中总变分用作正则化器。这个正则化器的迷人之处在于它能够允许变分模型的不连续求解，因此可以捕捉到对象边界。自这项杰出的工作以来，基于总变异的正则器已被用于处理不同的成像任务[8、14、15、17、19]。此外，在数学成像领域中，通过使用不同形式的正则化子，已经提出了许多变分模型[3，16，18，23，24，27，28]。

尽管ROF模型能有效去除噪声，同时保留物体边界，但它也有一些不理想的特性。例如，Meyer在文献[25]中指出，ROF模型无法保留图像对比度和物体边角，而在[7]中，Belletini、Caselles和Novaga研究了ROF模型可以维持什么样的形状，其中表明ROF模型会涂抹物体的角点。更重要的是，ROF模型还存在阶梯效应，即去噪后的图像会出现块状碎片或片状恒定区域，即使是给定图像中原本平滑的部分也不例外,这肯定会损害视觉效果。

为了解决阶梯现象，已经开发了相当多的高阶变分模型[9,18,23,31,35]，这是因为分段常数函数可能导致其二阶导数的幅度很大。准确地说，在[9]中，Bredies等人。开发了一个称为总广义变分的新术语，作为处理数学成像中的逆问题（包括图像去噪）的正则化器。由于这种新的正则化器利用高阶导数，因此所提出的模型成功地抑制了阶梯效应。在[18]中，Chan等人。建议添加非线性四阶扩散项以减少阶梯效应。在[23]中，不是全变分，而是直接将二阶导数纳入去噪模型中，因此也可以很大程度上消除块状现象。在[31]中，使用欧拉弹性体作为正则化器来达到图像去噪的目的，并且楼梯问题也得到了很好的解决。此外，在[35]中，作者提出使用图像表面平均曲率的 -范数作为噪声去除问题的正则化器。

尽管上述所有高阶模型都能成功地改善阶梯效应，但我们必须处理比ROF模型更复杂的模型。为这些高阶模型开发高效的数值方法往往具有挑战性，这在过去十年间吸引了大量研究人员的关注。许多高效的算法被开发出来，用于处理这些高阶、高度非线性和/或不可微的模型[4,13,20,3,34]。

在本文中，我们打算开发一种一阶图像去噪模型，以减少阶梯效应，同时去除噪声并有效保留物体边界。更准确地说，就像ROF一样，只有一阶导数模型才会被用于保持不连续性，ROF模型的显著特点是能够保留跳跃，这主要归功于其全变分正则化器。因此，对于噪声去除问题，我们仍然希望保留这一良好特性。然而，该正则化器无法避免阶梯效应，这个问题提醒我们，总变化可能无法恰当地应用于给定噪声图像中的每个区域。请注意，阶梯通常出现在图像强度梯度相对较小的位置，因为梯度较大的位置通常表示物体边界。从某种意义上说，总变化太弱而无法抑制平滑区域的块状效应。因此，为了减少阶梯现象，需要对这些区域（即梯度相对较小的区域）施加比总变化更高规则性的正则化器。基于这些论点，我们建议对图像梯度的不同区域使用不同类型的正则化器。具体来说，我们计划对小梯度区域应用p>1的图像梯度 -范数，同时保留大梯度区域的总变化。这种选择有助于减轻阶梯效应。例如，正如著名的Mumford-Shah模型[26]一样，如果选择梯度的 -范数作为正则化器，可以获得平滑的解。在这项工作中，我们仅对梯度较小的区域应用p>1的 -normof图像梯度，以减轻阶梯现象。
事实上，其他研究也提出了类似的想法[12,32]。在文献[12]中，Chang和Che考虑了三种总变分类型的图像去噪模型，其中使用了一阶偏导数的 -范数作为正则项，p=1/2,1,2，然后通过对来自三个模型的结果进行组合来获得去噪图像，以保持每个模型的优点。在文献[32]中，Vese研究了一类基于总变分的图像去噪和去模糊模型。具体来说，她建议使用 作为正则化器，而不是总变分 ，其中 是一些专门设计的函数。在这项工作中，Vese在有界变分函数空间中证明了相应模型的最小化者的存在性和唯一性，并对所提出的模型在势函数 的情况下进行了数值检验，以用于图像去噪和去模糊。事实上，本文将要讨论的模型可视为Vese工作中的特例[32]。不过，我们的工作重点在于，我们的模型除了能有效去除噪声和保留边缘外，还能减少阶梯效应。此外，我们模型中使用的势函数 与Vese工作中进行数值测试的势函数不同。
为了最小化我们的模型，我们建议便用增强拉格朗日方法(AIM.21,29]。最近，ALM已成功应用于非可微、非线性和高阶变分模型[5,31,34,36-38]。使用ALM的一个诱人之处在于，我们模型的最小化相当于寻找一些增广拉格朗日函数的鞍点，这样，我们的模型的最小化可以通过反复和交替地最小化一些相对简单的泛函来实现。事实上，这些泛函要么具有封闭式解，要么可以使用FFT等快速求解器来求解。
正如后面所讨论的，所提出的模型只涉及一阶导数，它可以被视为ROF模型的一个变体。因此，人们可能不期望所提出的模型能够达到那些高阶模型[9,18,22,31,35]的效果。不过，在数值成本与ROF几乎相同的情况下，所提出的模型可以减轻阶梯效应，同时还能去除噪声并保留边缘。

本文的其余部分安排如下。在下一节中，我们将介绍噪声去除问题的变分模型，其中基于全变分的正则化器是根据图像梯度分段定义的。在第3节中，我们讨论如何使用ALM最小化所提出的模型，然后进行数值算法的收敛性分析。然后，我们在第4节中介绍了数值实验，验证了所提出模型的特征，特别是阶梯效应的减少，第5节专门讨论了我们的结论。

2 基于全变分的图像去噪模型

正如引言中所讨论的，通过应用ROF模型，阶梯现象通常是不可避免的，这主要是由于基于全变分的正则化器。请注意，这种效果通常发生在图像强度梯度相对较小的区域，因为梯度较大的位置通常指的是对象边界。因此，为了减少阶梯效应，应该施加一些比总变差更强的正则化器。同时，我们还希望保留大梯度区域的总变化，以保留对象边界。基于此讨论，我们提出图像去噪问题的以下函数的最小化：

其中p>1，势函数 如下：

这里，参数a定义具有小或大梯度的区域。通过这个参数a，域将被分解为两部分。一方面，在 的区域，采用总变分作为正则化器以保持边缘。事实上， 沿着边缘取很大的幅度。另一方面，在 的区域， 的某个更高次幂用于在这样的区域中对u施加平滑约束。例如，当p=2时，在该区域中，相关的欧拉-拉格朗日方程为 ，则函数u应该是平滑的，这说明此类正则化器可以减轻阶梯效应。请注意，阶梯效应通常在梯度相对较小的区域中观察到。
我们可以很容易地检查函数 在p>1时在R上是凸的。我们在图1中分别展示了当p=1、3/2、2时a=2时该函数的图形以进行说明。p=1的情况对应于原始总变分正则化器的函数。事实上，Vese的工作[32]中明确给出了p=2的情况。此外，对于这种情况， 是Huber函数[22]，它也是函数 的莫罗包络线。
对于所提出的模型（方程1）的分析研究，可以遵循Vese的工作[32]中的讨论。我们这里只提出要点，详细的讨论可以在[2,32]中找到。
设 ，则其分布梯度Du定义了一个Radon测度。根据Radon-Nikodym定理，可以分解 ，其中dx是Lebesgue测度， ，且 与 相互奇异。此外，如Ambrosio[1]所示，奇异部分 可以进一步分解为“跳跃”部分和“Cantor”部分。为此，我们定义近似上限 和下限 如下：

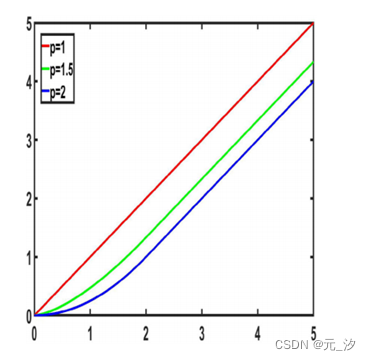
图1 在p = 1、3/ 2,2时分别为a = 2的曲线图
因此，如果 ，则对于勒贝格测度，几乎所有的点都是勒贝格点，即 。集合 ，它是勒贝格点集的补集。 是可数可校正的，并且可以定义 的正规 ，其中 表示一维的豪斯多夫测度。然后，在[1]中，Ambrosio表明

，
其中 是 的Cantor部分，可以得到以下结果：

正如[32]中所讨论的，所提出的模型（方程1）可以表示如下：

很容易看出，对于任何z>0，存在b>0，c>0，使得 。然后，根据Vese在[32]中的工作，可以得到以下存在性定理：
定理：泛函数 （方程2）在空间 中具有唯一的极小值。

3 所提出模型的增强拉格朗日方法

为了最小化泛函（1），可以直接求解其欧拉-拉格朗日方程，该方程可以表示为：

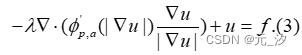
具体地，可以利用相关联的梯度流来找到该方程的解。
在这项工作中，我们打算使用增强拉格朗日方法（ALM）最小化泛函（1）。事实上，在过去的几年中，ALM已成功应用于最小化不可微分或/和高阶模型[31,34,36]。使用ALM最吸引人的特点是它的简单性，即可以将原始的最小化问题转化为约束优化问题，而后一问题的鞍点的寻找相当于重复地、交替地求解几个相对简单的泛函。准确地说，为了最小化泛函（1），如[34]中所示，我们提出了一个等效的约束优化问题如下：

并设计一个增广拉格朗日函数如下：

其中 是拉格朗日乘子， 是在数值实现中选择的惩罚参数。
根据优化理论，泛函(1)的极小值对应于增广拉格朗日泛函(5)的鞍点。为了找到鞍点，我们采用标准迭代策略，即通过固定另一个q和u来分别最小化每个q和u的相应子问题，然后更新拉格朗日乘子 ；这个过程将重复，直到两个变量收敛，这表明鞍点将被近似。算法1给出了近似泛函(5)鞍点的迭代方法。

具体来说，变量q和u需要最小化的两个子问题如下：

正如[31,34,36]中所讨论的， 的最小值由相应的欧拉-拉格朗日方程确定，如下所示：

这是一个具有常系数的线性椭圆方程，因此可以使用FFT来求解。
对于q的子问题，在这项工作中，我们只考虑p=32、2和3的情况。事实上， 的极小值）对于这三种情况都有闭式解。接下来，我们讨论p=2情况下 的极小值。对于p=2，势函数 如下：

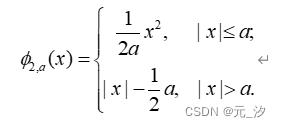
的极小值可以用下面的命题来描述。事实上，这个命题是优化中众所周知的事实[6]，可以使用近端映射来推导它。为了方便阅读，我们在这里保留一个直接证明。
命题 如果p=2，则 的极小值 给出如下：

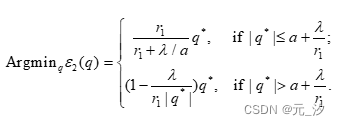
这里 .
证明请注意， 可以写成如下：

其中 ，且 独立于q。由于不涉及q的空间导数，我们可以通过逐点求被积函数的极小值来得到函数的极小值。为简单起见，将被积函数记为g(q)，即 。由于 是x≥0的增函数，因此很容易看出g(q)的极小值必须采用 的形式，其中s∈[0,1]。因此，我们只需要研究一个新函数 ，的极小值，其中 。为此，需要考虑以下两种情况：(1) ;(2) 。
情况1.如果 ，根据 的定义， 。可以发现 的最小值出现在 ，位于(0,1)内。
情况2.如果 ， 可以表示为：

容易看出 在 是上是凸的（注意 是凸的）。因此，h的最小值要么出现在两个端点，要么出现在临界点。与情况1一样，如果 ，即在区间 内， 在 处取最小值。人们可以检查 当且仅当 。换句话说，如果 ， 是 )在 中的临界点，因此是一个极小值。
类似地，对于 或 ， 在 时取最小值，如果 ，则等价于 。
结合上述两种情况，我们有如果 ，则 是 上 的最小值，而如果 ，则 为极小值。因此， 的极小值可表示为：

这就完成了证明。
我们这里仅导出p=2情况下的 最小值，事实上，对于 和p = 3情况也可以采用相同的过程。具体来说，于 情况下的最小值如下：

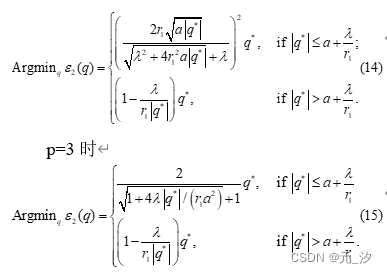
备注 事实上，正如[34]中所讨论的，ROF模型的子问题 具有如下形式：

它的最小化如下：

的定义如(12)中所示。可以看出，当 时，ROF模型允许其最小值为0。而对于新模型，仅当 时，最小化器才取0。这显示了两个模型之间的主要区别，也表明新模型能够减少阶梯现象。
在下文中，我们提供算法1中讨论的ALM的收敛结果。从变量u、q和 的初始猜测开始，可以得到一个序列 接下来，如[21,34]中，我们建立了在p=2的情况下序列 的收敛结果。事实上，在[10]中的离散设置中可以找到类似的收敛结果。
定理 令 为算法1中总结的算法生成的序列。如果 是一个鞍点增广拉格朗日函数 的点，则得到

证明 为方便起见，下文记 和 ，其中f,g可以是向量函数。
由于 是函数 的鞍点，即

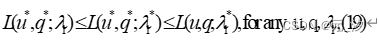
通过使用与[34]中相同的参数，可以得到 。由于 ，则对于函数 对任意 和 ，有 。因此

类似地，当 时，得到

由于 和 ， 使用相同的过程，可以得到以下结果：

和

为了方便表述，我们引入简短的符号 和 。然后，将(20)中的 、(22)中的 、(21)中的 、(23)中的 与上述四个不等 式相加，可得：

由于 且 该不等式简化如下：

进而

当 且 时，可得

由于不等式（23）对于 成立，我们也可以为 写出类似的不等式如下：

通过设置(23)中的 和(28)中的 将两个不等式相加，得出以下结果：

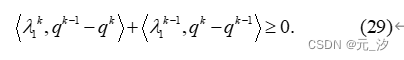
即， 。根据这个不等式，(27)可得出：

把下面这个式子

带入得到

由此可见，非负序列 是递减且收敛的，因此 。
备注 在这个证明中，我们只使用了 的凸性，因此该结论对于 的情况也成立。

4 数值实现

在本节中，我们介绍了在数值实现中求解方程（11）和更新变量q的细节，这与工作[31,34,36]中的类似。
设 为离散化图像域，每个点 为一个网格点。然后，我们定义具有周期性边界条件的离散后向和前向微分算子如下：

相应地定义了中心差分算子和梯度算子：

请注意等式。(11)是一个常系数椭圆方程，可以使用FFT来求解。为此，等式。(11)离散化如下：

其中g代表方程的右侧。(11)。对两边进行傅里叶变换，可得：

其中 和 。一旦计算出Fu，就可以利用离散傅里叶逆变换得到u。
对于 的极小值 ，注意它的两个分量分别定义在半网格 和 上，在数值实现中，我们分别计算 和 。具体而言，具有以下特点：

并且

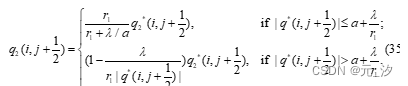
其中

。
变量u、q更新后，拉格朗日乘子 将在 处前进：

5 数值实验

在本节中，我们通过将所提出的模型应用于多个图像来进行数值实验，并将结果与使用ROF模型获得的结果进行比较，以展示如何减轻阶梯效应。
在这项工作中，我们主要将所提出的模型与ROF进行比较，因为所提出的模型只是ROF的一个变体，略有变化，并且如备注1中所述，这两个模型的数值成本几乎相同。由于所提出的模型仅采用一阶导数，人们可能不会期望它能够获得与那些高阶模型一样好的结果[9,18,23,31,35]。事实上，这些模型已被证明对于图像去噪或其他成像问题非常成功。为了评估所提出模型的性能，我们还将所提出的模型与Bredies等人著名的总广义变分（TGV）模型进行了比较。[9]，它产生了出色的去噪效果，同时还抑制了阶梯效应。
为了公平比较，我们还应用ALM来最小化ROF模型。事实上，ROF模型的算法与所提出的模型的算法的不同之处仅在于每次迭代中q的更新（参见备注1）。此外，我们为两个模型选择模型参数λ，使得它们去除的噪声部分f−u具有几乎相同的平均Frobenius范数，这将在后面定义。
如[31,36,38]中所示，为了监控迭代过程的收敛性，我们检查以下相对残差：

其中k指的是迭代次数， 是定义域的面积， 表示 上的范数。具体来说，对于图像 我们还跟踪拉格朗日乘子的相对误差如下：

解得 的相对误差

并检查能量 与迭代次数k的关系。这些相对误差的值可以用作终止迭代过程的停止标准。出于演示的目的，所有上述量均以对数刻度显示，如图1和2所示。7和8。
在本文提出的所有实验中，添加的噪声都是均值为零、标准差 的高斯噪声，即添加的噪声 。为了公平比较，我们采用弗罗贝尼乌斯范数来测量去除的部分。具体来说，对于 ，f的平均弗罗贝尼乌斯范数为 。然后，我们为我们的模型和ROF模型选择正则化参数，以便它们去除的噪声部分具有几乎相同的Frobenius范数。
我们首先考虑图2中的合成图像。清理后的图像表明，就像ROF一样，所提出的模型能够有效地去除噪声，同时保留跳跃或边缘。更重要的是，所提出的模型很大程度上减轻了阶梯效应。事实上，所提出模型的这些特征归功于所提出的正则化器。具体来说，沿着梯度较大的边缘，正则化器采用全变分的形式，因此可以保留边缘位置；而在梯度相对较小的区域，我们使用梯度的 范数作为p>1的正则化器，这比图像上的总变化具有更高的规则性。具体来说，当p=2时，相关的欧拉-拉格朗日方程在这些区域中包含拉普拉斯算子，这肯定有助于平滑图像。如前所述，阶梯现象是梯度相对较小的区域过度锐化的结果。因此，在这些区域中，我们建议添加比总变化更高的规律性要求，以减少阶梯效应。

图2无噪声卡通图像、有噪声卡通图像以及ROF和所提出的模型分别p=1.5、2、3的去噪图像。在本实验中，添加噪声的标准差为 。对于我们的模型和模型，添加噪声n的范数为 ，对于我们的模型和ROF，移除的噪声部分的范数
在图3中，我们将我们的模型应用于p=1.5,2,3的真实图像“Barbara”。结果再次证明所提出的模型能够消除噪声并保持边缘。此外，不同p的结果之间不存在显着差异。然而，参数a的选择是不同的。具体来说，我们使用a=8表示p=1.5，a=5表示p=2，a=4表示p=3。这是因为当p很大时，我们缩小了施加p−拉普拉斯算子的区域为了避免过度平滑，而当p很小时，我们用新的正则化器扩展区域。

图3无噪声图像“Barbara”、噪声图像以及通过ROF和所提出模型分别p=1.5、2、3进行去噪的图像。在本实验中，添加噪声的标准差为σ=10。对于我们的模型和ROF，添加噪声n的范数为 ，去除噪声部分的范数为
为了更好地进行比较，图4中展示了两个模型获得的放大的“额头”，这表明所提出的模型充分改善了楼梯效应。

图4ROF模型和所提出的模型获得的放大“额头”部分的比较，p分别为1.5、2、3。ROF的结果中清楚地呈现了阶梯效应，而新模型则大大减少了阶梯效应
为了进一步测试所提出的模型，在图5中，我们展示了两个模型在不同水平的高斯噪声下获得的放大的“前额”部分，即 分别=10、15和20。这些结果再次表明所提出的模型能够很大程度上缓解阶梯效应。然而，一旦噪声水平（ ）很高，就会影响所提出模型的输出。在这些实验中，由于我们使用相同的参数a=5，因此如果在某些区域添加的噪声较高，则将采用基于全变分的正则化器，并且平滑效果将减弱，从而在“前额。”我们当然可以选择一个大的正则化参数λ来消除这样的脊；然而，它也可能过度平滑一些有意义的信号。因此，从这个意义上说，所提出的模型更适用于噪声水平相对较低的图像，例如标准差 =10。
在图6中，我们使用不同的参数a比较了p=2和 =10时所提出模型的性能。结果表明，如果a=2，则“额头”上存在一些脊，而当a=8时，去噪图像看起来比选择a=5更模糊。事实上，如果a很小，则提出的模型为接近ROF，因为只有某些区域被施加了新的正则化器，这解释了为什么去噪图像仍然保留脊线；如果a很大，则拉普拉斯算子将应用于很大的区域，从而过度平滑该区域中的信号。

图5在不同高斯噪声水平 =10、15、20下，ROF模型与p=2的提出模型获得的放大“前额”部分的比较（从左到右）。ROF的结果中清楚地呈现了楼梯效应，而新模型则大大减少了楼梯效应

图6对于受高斯噪声σ=10污染但a=2、5、8不同的图像，p=2时所提出的模型获得的放大“额头”部分的比较（从左到右）
为了显示所提出的ALM迭代过程的收敛性，在图7中，我们列出了相对残差(36)、拉格朗日乘数的相对误差(37)、 的相对误差(38)和能量 与迭代的比较，通过应用所提出的模型，其中p=2为“Barbara”， =10。请注意，经过1000次迭代后，uk的相对误差小至3.13×10−16，接近精度Matlab中的浮点数。这些结果表明迭代过程收敛到增广拉格朗日函数（方程5）的鞍点，从而达到所提出模型的最小化。

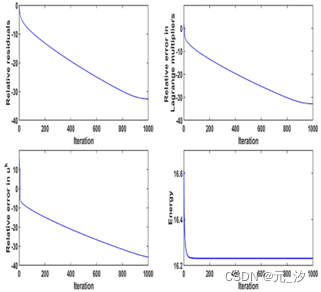
图7使用 =10的高斯噪声污染的示例“Barbara”的相对残差(36)、拉格朗日乘子相对误差(37)、 (38)的相对误差和能量 的图我们的模型p=2。所有数量均以对数刻度表示。请注意， 的相对误差达到3.13×10−16，接近Matlab中浮点数的精度
在图8中，我们还展示了当应用于 =10的“Barbara”时，ROF模型和提出的模型（p=2）的 相对误差与迭代的关系图。这些图表明，通过使用ALM，所提出的模型有很强的收敛到极小值的倾向，而ROF模型在经过一些迭代后可能会出现缓慢的收敛。这主要是由于对于梯度相对较小的区域使用了强凸正则化器，即L2正则化器。
在图中。如图9和10所示，我们将所提出的模型应用于另一个真实图像“辣椒”。这些结果再次证明该模型能够有效地去除噪声并保持边缘，同时还能减轻阶梯效应。具体来说，在选定的放大区域中，所提出的模型可以成功地保留辣椒上的阴影。

图8当应用于 =10的“Barbara”时，ROF模型和p=2的建议模型在 (38)中的相对误差收敛性的比较。请注意，垂直量以对数刻度显示

图9无噪声图像“peppers”、噪声图像以及通过ROF和p=1.5、2、3的建议模型分别进行去噪的图像。在本实验中，添加噪声的标准差为 =10。对于我们的模型和ROF，添加噪声n的范数为 ，去除噪声部分的范数为

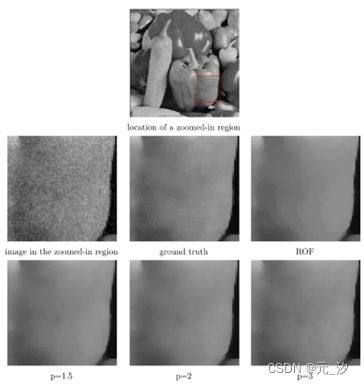
图10ROF模型和所提出的模型获得的“辣椒”放大图块的比较，p分别为1.5、2、3。ROF的结果中清楚地呈现了阶梯效应，而新模型则大大减少了阶梯效应
为了进一步比较两个模型清理图像的质量，我们在表1中列出了上述实验的峰值信噪比（PSNR）和结构相似性指数测量（SSIM）[33]。PSNR和SSIM是评估去噪图像质量的两种常用的客观图像指标。事实上，PSNR衡量的是无噪声图像和去噪图像之间的均方差。由于它是基于最小二乘的度量，因此它更喜欢过度平滑的结果。另一方面，SSIM考虑了以下三个比较：亮度、对比度和结构[33]，因此它测量了高频信号的相似性，例如两幅图像之间的边缘。从表1可以看出，ROF产生的PSNR略高于所提出的模型。然而，很容易看出所提出的模型产生比ROF更高的SSIM。

图11TGV（总广义变异）模型[9]与p=2时提出的模型的比较。两个模型的加性噪声和去除噪声部分的范数如下：‖n‖F=15.03，对于第一个示例， ， 对于第二个示例 ， ;第三个例子 ，

图12通过TGV（总广义变异）模型[9]获得的“Barbara”和“peppers”的放大斑块与高斯噪声水平 =10时p=2的建议模型的比较
在图中。如图11和图12所示，我们进一步比较了p=2时所提出的方法和著名的TGV（总广义变异）模型[9]获得的结果，以及表1中的PSNR和SSIM的相关值。比较起来，对于每个模型和每个实验，加性噪声和去除噪声部分几乎具有相同的范数。正如预期的那样，这些数字证明TGV生成的解比所提出的模型更平滑，因为它使用更高阶导数，并且如表1所示，TGV还导致比所提出的模型更高的PSNR和SSIM值。另一方面，仔细检查图中的图。从图11和图12可以看出，特别是对于“卡通”图像和“芭芭拉”“额头”的右上部分，可以看到TGV产生了稍微过度平滑的结果。此外，由于TGV模型涉及二阶导数，因此它通常比所提出的模型需要更多的计算工作。

6结论

在本文中，我们考虑一种变分图像去噪模型，旨在改善众所周知的ROF模型固有的阶梯效应。与ROF模型不同的是，该模型对图像强度梯度大小不同的区域应用不同类型的正则化器，因此可以像ROF一样保留边缘，而平滑区域不会被过度锐化。为了最小化相关函数，我们使用增强拉格朗日方法开发了一种快速算法。还提供了所提出算法的收敛性分析。列出了数值经验来证明所提出模型的特征，并证明所提出算法的效率。

致谢作者衷心感谢匿名审稿人提出的宝贵意见和建议，这些意见和建议对改进本文的表达有很大帮助。

参考文献

[1] Ambrosio,L.:Acompactnesstheoremforanewclassoffunctionsofboundedvariation.BollettinodellaUnioneMatematicaItalianaVII(4),857–881(1989)
[2] Aubert,G.,Kornprobst,P.:Mathematicalproblemsinimageprocessing:partialdifferentialequationsandthecalculusofvariations.SpringerScienceandBusinessMedia(2006)
[3] Aubert,G.,Vese,L.:Avariationalmethodinimagerecovery.SIAMJ.Numer.Anal.34(5),1948–1979(1997)
[4] Brito-Loeza,C.,Chen,K.:Multigridalgorithmforhighorderdenoising.SIAMJ.Imaging.Sciences3(3),363–389(2010)
[5] Bae,E.,Tai,X.C.,Zhu,W.:AugmentedLagrangianmethodforanEuler’selasticabasedsegmentationmodelthatpromotesconvexcontours.InverseProbl.Imag.11(1),1–23(2017)
[6] Beck,A.:First-OrderMethodsinOptimization,vol.25,SIAM(2017)
[7] Bellettini,G.,Caselles,V.,Novaga,M.:ThetotalvariationflowinRn.J.Differ.Equations184,475–525(2002)
[8] Bertalmio,M.,Vese,L.,Sapiro,G.,Osher,S.:Simultaneousstructureandtextureimageinpainting.IEEETrans.onImageProcess.12(8),882–889(2003)
[9] Bredies,K.,Kunisch,K.,Pock,T.:Totalgeneralizedvariation.SIAMJ.ImagingSci.3(3),492–526(2010)
[10] Boyd,S.,Parikh,N.,Chu,E.,Peleato,B.,Eckstein,J.:Distributedoptimizationandstatisticallearningviathealternatingdirectionmethodofmultipliers.FoundationsandTrendsinMachinelearning3(1),1–122(2011)
[11] Buttazzo,G.:Semicontinuity,relaxationandintegralrepresentationinthecalculusofvariations,PitmanResearchNotesinMathematics207,LongmanScientificandTechnical(1989)
[12] Chang,Q.S.,Che,Z.Y.:AnadaptivealgorithmforTV-basedmodelofthreenormsLq,(q=12,1,2)inimagerestoration.AppliedMathandComput.329,251–265(2018)
[13] Chambolle,A.,Pock,T.:Afirst-orderprimal-dualalgorithmforconvexproblemswithapplicationstoimaging.J.MathImagingVis.40,120–145(2011)
[14] Chan,T.,Esedoglu,S.:Aspectsoftotalvariationregularizedl1functionapproximation.SIAMJ.Appl.Math.65(5),1817–1837(2005)
[15] Chan,T.,Esedoglu,S.,Park,F.,Yip,M.H.:Recentdevelopmentsintotalvariationimagerestoration.In:Paragios,N.,Chen,Y.,Faugeras,O.(eds.)HandbookofMathematicalModelsinComputerVision.Springer,Berlin(2005)
[16] Chambolle,A.,Lions,P.L.:Imagerecoveryviatotalvariationminimizationandrelatedproblems.Numer.Math.76,167–188(1997)
[17] Chan,T.,Shen,J.:Mathematicalmodelsforlocalnontextureinpaintings.SIAMJ.Appl.Math.62(3),1019–1043(2001)
[18] Chan,T.,Marquina,A.,Mulet,P.:High-ordertotalvariation-basedimagerestoration.SIAMJ.Sci.Comput.22(2),503–516(2000)
[19] Chan,T.,Wong,C.K.:Totalvariationblinddeconvolution.IEEETrans.ImageProcess.7(3),370–375(1998)
[20] Goldstein,T.,Osher,S.:ThesplitBregmanmethodforL1-regularizedproblems.SIAMJ.ImagingSci.2,323–343(2009)
[21] Glowinski,R.,LeTallec,P.:AugmentedLagrangianandOperator-splittingMethodsinNonlinearMechanics.SIAM,Philadelphia(1989)
[22] Huber,P.J.:Robustestimationofalocationparameter.Ann.Stat.53(1),73–101(1964)
[23] Lysaker,M.,Lundervold,A.,Tai,X.C.:Noiseremovalusingfourth-orderpartialdifferentialequationwithapplicationstomedicalmagneticresonanceimagesinspaceandtime.IEEE.Trans.ImageProcess.12,1579–1590(2003)
[24] Lysaker,M.,Osher,S.,Tai,X.C.:Noiseremovalusingsmoothednormalsandsurfacefitting.IEEE.Trans.ImageProcess.13(10),1345–1457(2004)
[25] Meyer,Y.:Oscillatingpatternsinimageprocessingandnonlinearevolutionequations,UniversityLectureSeries,Vol22,Amer.Math.Soc.
[26] Mumford,D.,Shah,J.:Optimalapproximationbypiecewisesmoothfunctionsandassociatedvariationalproblems.Comm.PureAppl.Math.42,577–685(1989)
[27] Osher,S.,Burger,M.,Goldfarb,D.,Xu,J.J.,Yin,W.T.:Aniterativeregularizationmethodfortotalvariation-basedimagerestoration.MultiscaleModel.Simul.4,460–489(2005)
[28] Osher,S.,Sole,A.,Vese,L.:Imagedecompositionandrestorationusingtotalvariationminimizationandtheh−1norm.SIAMMultiscaleModel.Simul.1,349–370(2003)
[29] Rockafellar,R.T.:AugmentedLagrangiansandapplicationsoftheproximalpointalgorithminconvexprogramming.Math.Oper.Res.1(2),97–116(1976)
[30] Rudin,L.,Osher,S.,Fatemi,E.:Nonlineartotalvariationbasednoiseremovalalgorithm.Phys.D60,259–268(1992)
[31] Tai,X.C.,Hahn,J.,Chung,G.J.:AfastalgorithmforEuler’sElasticamodelusingaugmentedLagrangianmethod.SIAMJ.ImagingSciences4(1),313–344(2011)
[32] Vese,L.:AstudyintheBVspaceofadenoising-deblurringvariationalproblem.Appl.MathOptim.44,131–161(2001)
[33] Wang,Z.,Bovik,A.C.,Sheikh,H.R.,Simoncelli,E.P.:Imagequalityassessment:fromerrorvisibilitytostructuralsimilarity.IEEE.Trans.ImageProcess.13(4),600–612(2004)
[34] Wu,C.,Tai,X.C.:AugmentedLagrangianmethod,dualmethods,andsplitBregmaniterationforROF,VectorialTV,andhighordermodels.SIAMJ.ImagingSciences3(3),300–339(2010)
[35] Zhu,W.,Chan,T.:Imagedenoisingusingmeancurvatureofimagesurface.SIAMJ.ImagingSciences5(1),1–32(2012)
[36] Zhu,W.,Tai,X.C.,Chan,T.:AugmentedLagrangianmethodforameancurvaturebasedimagedenoisingmodel.InverseProbl.Imag.7(4),1409–1432(2013)
[37] Zhu,W.,Tai,X.C.,Chan,T.:ImagesegmentationusingEuler’selasticaastheregularization.J.Sci.Comput.57(2),414–438(2013)
[38] Zhu,W.:AnumericalstudyofameancurvaturedenoisingmodelusinganovelaugmentedLagrangianmethod.InverseProbl.Imag.11(6),975–996(2017)