[NOIP2002 普及组] 过河卒【暴搜+DP详解+解析时间复杂度】

😊😊 😊😊
不求点赞，只求耐心看完，指出您的疑惑和写的不好的地方，谢谢您。本人会及时更正感谢。希望看完后能帮助您理解算法的本质
😊😊 😊😊

[NOIP2002 普及组] 过河卒

题目描述

棋盘上 $A$ 点有一个过河卒，需要走到目标 $B$ 点。卒行走的规则：可以向下、或者向右。同时在棋盘上 $C$ 点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。

棋盘用坐标表示，$A$ 点 $(0,0)$、$B$ 点 $(n,m)$，同样马的位置坐标是需要给出的。

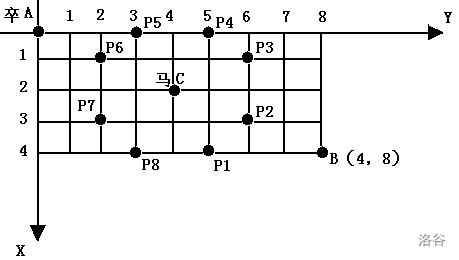
现在要求你计算出卒从 $A$ 点能够到达 $B$ 点的路径的条数，假设马的位置是固定不动的，并不是卒走一步马走一步。

输入格式

一行四个正整数，分别表示 $B$ 点坐标和马的坐标。

输出格式

一个整数，表示所有的路径条数。

样例 #1

样例输入 #1

6 6 3 3

样例输出 #1

6

提示

对于 $100\%$ 的数据，$1\le n,m\le 20$，$0\le$ 马的坐标 $\le 20$。

【题目来源】

NOIP 2002 普及组第四题

小白到进阶各种解法：

一、暴搜：详细分析在DP阶段，可以先看DP，易懂😊

代码：

#include<iostream>

using namespace std;
const int N = 23;
int st[N][N];
int dx[] = {-2, -2, -1, 1, 2, 2, 1, -1};
int dy[] = {-1, 1, 2, 2, 1, -1, -2, -2};
int b1, b2, m1, m2;
int ans;

void dfs(int x, int y)
{
	if (x == b1 && y == b2)
	{
		ans ++;
		return ;
	}
	
	//两个方向上去搜索！
	if (x+1<=b1 && st[x+1][y]==0)	//没有越界，并且下一个点不是障碍物！	往下走！
		dfs (x+1, y);
		
	if (y+1<=b2 && st[x][y+1]==0)	//往右走 
		dfs (x, y+1);
}

int main()
{
	cin >> b1 >> b2 >> m1 >> m2;    //输入的是B点坐标及马的坐标！
	st[m1][m2] = true;  //标记为true！
    
    //标记由该马所引发的所有障碍物！
    //共8个方向！
    for (int i=0; i < 8; i ++)
    {
        int a = m1 + dx[i], b = m2 + dy[i];
        if (a >= 0 && a <= b1 && b >= 0 && b <= b2)
            st[a][b] = 1;
    }
    
    dfs (0, 0);
    cout << ans << endl;
    
	return 0;
}

二、记忆化搜索：待更新😊

代码：AC不了！有错！

#include<iostream>
#include<cstring>
#include<algorithm>

using namespace std;
const int N = 23;
int st[N][N];
int dx[] = {-2, -2, -1, 1, 2, 2, 1, -1};
int dy[] = {-1, 1, 2, 2, 1, -1, -2, -2};
int b1, b2, m1, m2;
long long f[N][N];f[x][y]表示从(x,y)走到终点的方案数！	
开longlong：走到(n,m)点一共要走（n+m）步，所以说先从n+m里面选出n步，剩余的步数就是向下的了，方案数为：C(n+m,n); 

long long dfs(int x, int y)
{
	if (f[x][y] != -1) 	若下次走到同样的点时，就直接返回之前的方案数，再走一遍也是一样的！
		return f[x][y];
	
	if (x == b1 && y == b2)	//走到终点，给xy赋值为1，表示从当前点走到终点的方案为1；
		return 1;
	
	//两个方向上去搜索！
	if (x+1<=b1 && st[x+1][y]==0)	//没有越界，并且下一个点不是障碍物！	往下走！
		f[x][y] += dfs (x+1, y);
		
	if (y+1<=b2 && st[x][y+1]==0)	//往右走 
		f[x][y] += dfs (x, y+1);
	return f[x][y];
}

int main()
{
	cin >> b1 >> b2 >> m1 >> m2;    //输入的是B点坐标及马的坐标！
	st[m1][m2] = true;  //标记为true！
    
    //标记由该马所引发的所有障碍物！
    //共8个方向！
    for (int i=0; i < 8; i ++)
    {
        int a = m1 + dx[i], b = m2 + dy[i];
        if (a >= 0 && a <= b1 && b >= 0 && b <= b2)
            st[a][b] = 1;
    }
    
    cout << dfs (0, 0);
    
	return 0;
}

三、本题考察算法：动态规划😊

思路：

---

时间复杂度的分析：

首先解释为何本题的方案数会爆 $int$：

在这个题目中，我们需要求出卒从 (0,0) 点走到 (n, m)点的方案数。因为卒每次只能向
右或者向下走，所以它一共需要向右走 n 步，向下走 m 步。而我们只需要确定在这(n
+m)中，选择哪 n 步向右走，其余的就必须向下走。

所以，总方案数就是在 $n+m$ 步中选择 n 步向右走的方案数，即：C（n+m，n）步；组合数公式如下图；

当 n=20, m=20的时候，直接计算结果为：137846528820，超过了 int 的范围，会导致计算结果出错。

所以说我们需要用 long long 来存储这个结果。

若本题用暴搜的话会超时：
因为搜索的时间复杂度是指数级别的，随着棋盘大小的增加，搜索的状态数会呈指数级别增长，导致搜索时间过长。因此需要采用其他算法，比如动态规划。

搜索算法的时间复杂度取决于搜索空间的大小和搜索算法的策略。在搜索的过程中，每个节点可能有多个子节点需要遍历，因此搜索的时间复杂度会随着搜索空间的增加而增加。

对于一般的搜索问题，搜索空间往往非常大，尤其是在状态数量呈指数增长的情况下。例如，在本题中，每个位置上可能有卒或马或者空位三种状态，棋盘大小为 $n\times m$，搜索空间的大小为 $3^{n\times m}$，在 $n,m$ 比较大的情况下，这个搜索空间的大小会非常庞大，因此暴力搜索的时间复杂度就会呈指数级别增长，很容易超时。

因此，在这种情况下，我们需要设计更加高效的搜索策略和剪枝技巧，来尽可能减少搜索空间的大小，减少搜索的时间复杂度。

假设棋盘大小为 $n\times m$，卒初始位置为 $A(x_0,y_0)$，目标位置为 $B(x_B,y_B)$，马的位置为 $H(x_H,y_H)$。

我们可以将搜索算法看作一个树形结构，其中每个节点表示卒在棋盘上的一个位置，每个节点的子节点表示卒从该位置走一步所能到达的位置。在这个树形结构中，每个节点的出度不超过 $2$（因为卒只能向下或向右走），因此树形结构的最大深度不会超过 $n+m$。

对于每个节点，我们需要判断它是否合法（即是否在棋盘内且不被马所控制），因此每个节点的时间复杂度为 $O(1)$。因为树形结构的最大深度为 $n+m$，因此整个搜索的时间复杂度为 $O((n+m{)}^2)$。

需要注意的是，虽然搜索算法的时间复杂度是多项式级别的，但由于本题的棋盘较小，搜索树的分支因子较小，因此搜索算法仍然可以在规定时间内解决本题。

---

分析完时间复杂度后，我们开始来实现本题：

1. 本题为二维平面上求方案数模型，对于终点$（n，m）$，我们不妨思考其是如何转移而来的，终点 (n, m) 的最后一步转移由两个选择，分别是由：$(n-1,m),(n,m-1)$ 所转移来的。而我们要求的是方案数：所以到达 $(n,m)$ 的方案数 = 到达 $(n,m-1)$ 的方案数 + 到达$(n-1,m)$的方案数之和。而 $(n-1,m)和(n,m-1)$的方案数又是如何得到的呢？
2. 所以说我们继续向上思考，$(n-1,m),(n,m-1)$ 又是如何转移得到的了？这不就是可以构造出子问题推导大问题了吗？并且子问题的求解不受后面的问题求解的影响，也符合打表推导的性质，所以 ⇒ DP。
3. 既然是二维平面则状态方程也可以设为二维的：
   $f[i][j]：$表示从起点到 $(i,j)$ 的方案数。
4. 状态计算：$f[i][j]=f[i-1][j]+f[i][j-1]；$

代码：

#include<iostream>
#include<cstring>
#include<algorithm>

using namespace std;
const int N = 100;
int st[N][N];   //标记障碍物！
long long f[N][N];
int dx[] = {-2, -2, -1, 1, 2, 2, 1, -1};
int dy[] = {-1, 1, 2, 2, 1, -1, -2, -2};

int main()
{
    int b1, b2, m1, m2;
    cin >> b1 >> b2 >> m1 >> m2;    //输入的是B点坐标及马的坐标！
    
    //马的坐标也是障碍物！
    st[m1][m2] = true;  //标记为true！
    
    //标记由该马所引发的所有障碍物！
    //共8个方向！
    for (int i=0; i < 8; i ++)
    {
        int a = m1 + dx[i], b = m2 + dy[i];
        if (a >= 0 && a <= b1 && b >= 0 && b <= b2)
            st[a][b] = 1;
    }
    
    //初始化边界：
    //有8列！
    for (int i=0; i <= b2; i ++)
    {
        if (st[0][i]) break;
		f[0][i] = true; 
    }
    
    //有4行：
    for (int i=0; i <= b1; i ++)
    {
        if (st[i][0]) break;
        f[i][0] = true;
    }
    
    //开始递推： 
    for (int i=1; i <= b1; i ++)
    {
    	for (int j=1; j <= b2; j ++)
    	{
    		if (st[i][j]) continue;
    		f[i][j] = f[i-1][j] + f[i][j-1];
		}
	}

    cout << f[b1][b2] << endl;
    return 0;
}