论文复现——Low-level算法 NAFNet (去噪)
Simple Baselines for Image Restoration——一个简单的用于图像恢复的强基线模型
官方源码:https://github.com/megvii-research/NAFNet
复现地址:https://github.com/kongdebug/NAFNet-pd
脚本任务:https://aistudio.baidu.com/aistudio/clusterprojectdetail/4460788
PaddleGAN版本:https://github.com/PaddlePaddle/PaddleGAN/blob/develop/docs/zh_CN/tutorials/swinir.md
1. 简介
1.1 项目背景
NAFNet是旷视研究院提出的用于图像复原的模型,在图像去模糊、去噪都取得了很好的性能,不仅计算高效同时性能显著优于之前SOTA方案。
基于NAFNet的改进或应用在其他比赛中依然获得了很好的成绩,例如在百度网盘AI大赛去模糊赛道获得第一名的方案百度网盘AI大赛-模糊文档图像恢复比赛第1名方案,以及去遮挡赛道的第一名百度网盘AI大赛-文档图片去遮挡第1名,都使用了NAFNet网络,可见其强悍的性能。
此外,如何用NAFNet作去模糊,可以看孔宝的项目使用PaddleGAN中的NAFNet进行图像去模糊
。
1.2 算法详解

NAFNet提出一种超简基线方案Baseline,它不仅计算高效同时性能优于之前SOTA方案;在所得Baseline基础上进一步简化得到了NAFNet.

基于Restormer的模块示意图,NAFNet设计另一种最简洁的模块方案,具体体现在:
-
首先给出PlainNet,去掉self-attention,去掉门控机制,就是最简单的深度卷积+ReLU激活。
-
接着设计Baseline网络,借鉴Trasnformer中使用LN可以使得训练更平滑。Baseline中同样引入LN操作。
-
在Baseline方案中使用GELU和CA联合替换ReLU,GELU可以保持降噪性能相当且大幅提升去模糊性能。
-
由于通道注意力的有效性已在多个图像复原任务中得到验证。NAFNet提出了两种新的注意力模块组成即SCA和SimpleGate模块,具体如下所示:
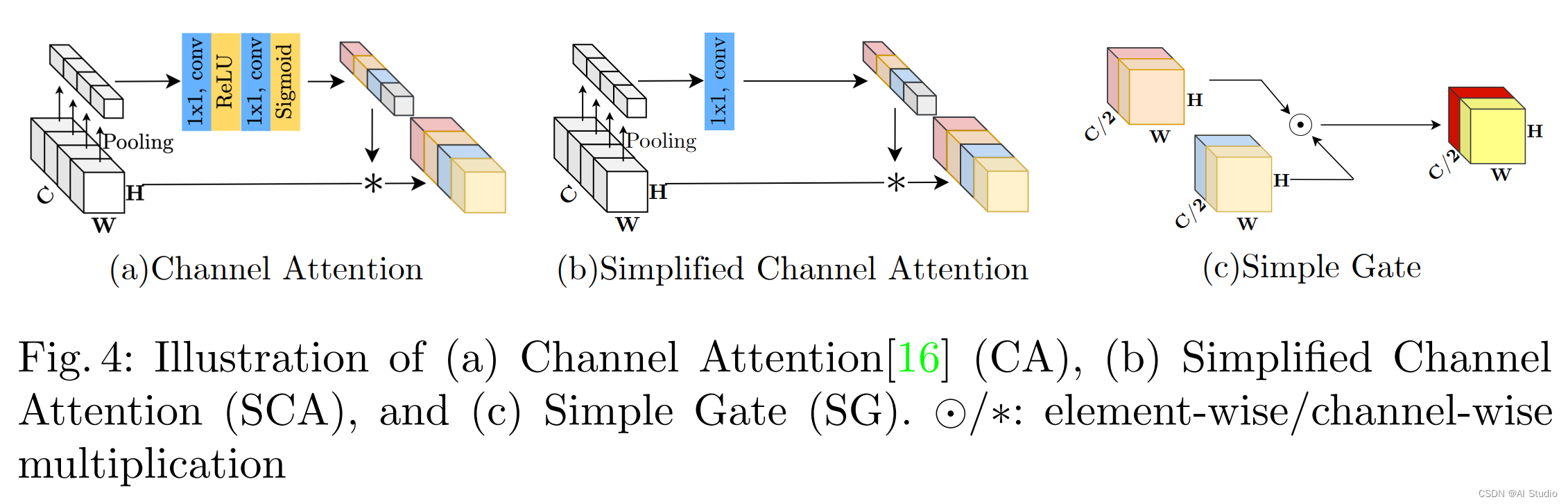
其中SCA(见上图b)直接利用1x1卷积操作来实现通道间的信息交换。而SimpleGate(见上图c)则直接将特征沿通道维度分成两部分并相乘。
作者大胆猜想,GELU可以看作是SampleGate的特例,SampleGate可以当作是一种广义的非线性激活方式,从而替换掉现在的非线性激活函数。移除了非线性激活单元且性能进一步提升。
NAFNet在SIDD降噪与GoPro去模糊任务上均达到了新的SOTA性能,同时计算量大幅降低。
对模型更详细的介绍,可参考论文原文 Simple Baselines for Image Restoration ,PaddleGAN 中目前提供去噪任务的权重
1.3 核心代码
展示NAFNet的一些核心代码。
层归一化方法如下:
import paddle
from paddle import nn as nn
from paddle.autograd import PyLayer
class SimpleGate(nn.Layer):
def forward(self, x):
x1, x2 = x.chunk(2, axis=1)
return x1 * x
class LayerNormFunction(PyLayer):
@staticmethod
def forward(ctx, x, weight, bias, eps):
ctx.eps = eps
N, C, H, W = x.shape
mu = x.mean(1, keepdim=True)
var = (x - mu).pow(2).mean(1, keepdim=True)
y = (x - mu) / (var + eps).sqrt()
ctx.save_for_backward(y, var, weight)
y = weight.reshape([1, C, 1, 1]) * y + bias.reshape([1, C, 1, 1])
return y
@staticmethod
def backward(ctx, grad_output):
eps = ctx.eps
N, C, H, W = grad_output.shape
y, var, weight = ctx.saved_tensor()
g = grad_output * weight.reshape([1, C, 1, 1])
mean_g = g.mean(axis=1, keepdim=True)
mean_gy = (g * y).mean(axis=1, keepdim=True)
gx = 1. / paddle.sqrt(var + eps) * (g - y * mean_gy - mean_g)
return gx, (grad_output * y).sum(axis=3).sum(axis=2).sum(axis=0), grad_output.sum(axis=3).sum(axis=2).sum(
axis=0)
class LayerNorm2D(nn.Layer):
def __init__(self, channels, eps=1e-6):
super(LayerNorm2D, self).__init__()
self.add_parameter('weight', self.create_parameter([channels],
default_initializer=paddle.nn.initializer.Constant(
value=1.0)))
self.add_parameter('bias', self.create_parameter([channels],
default_initializer=paddle.nn.initializer.Constant(value=0.0)))
self.eps = eps
def forward(self, x):
return LayerNormFunction.apply(x, self.weight, self.bias, self.eps)
NAFBlock 代码如下:
class NAFBlock(nn.Layer):
def __init__(self, c, DW_Expand=2, FFN_Expand=2, drop_out_rate=0.):
super().__init__()
dw_channel = c * DW_Expand
self.conv1 = nn.Conv2D(in_channels=c, out_channels=dw_channel, kernel_size=1, padding=0, stride=1, groups=1,
bias_attr=True)
self.conv2 = nn.Conv2D(in_channels=dw_channel, out_channels=dw_channel, kernel_size=3, padding=1, stride=1,
groups=dw_channel,
bias_attr=True)
self.conv3 = nn.Conv2D(in_channels=dw_channel // 2, out_channels=c, kernel_size=1, padding=0, stride=1,
groups=1, bias_attr=True)
# Simplified Channel Attention
self.sca = nn.Sequential(
nn.AdaptiveAvgPool2D(1),
nn.Conv2D(in_channels=dw_channel // 2, out_channels=dw_channel // 2, kernel_size=1, padding=0, stride=1,
groups=1, bias_attr=True),
)
# SimpleGate
self.sg = SimpleGate()
ffn_channel = FFN_Expand * c
self.conv4 = nn.Conv2D(in_channels=c, out_channels=ffn_channel, kernel_size=1, padding=0, stride=1, groups=1,
bias_attr=True)
self.conv5 = nn.Conv2D(in_channels=ffn_channel // 2, out_channels=c, kernel_size=1, padding=0, stride=1,
groups=1, bias_attr=True)
self.norm1 = LayerNorm2D(c)
self.norm2 = LayerNorm2D(c)
self.drop_out_rate = drop_out_rate
self.dropout1 = nn.Dropout(drop_out_rate) if drop_out_rate > 0. else None # nn.Identity()
self.dropout2 = nn.Dropout(drop_out_rate) if drop_out_rate > 0. else None # nn.Identity()
self.add_parameter("beta", self.create_parameter([1, c, 1, 1],
default_initializer=paddle.nn.initializer.Constant(value=0.0)))
self.add_parameter("gamma", self.create_parameter([1, c, 1, 1],
default_initializer=paddle.nn.initializer.Constant(
value=0.0)))
def forward(self, inp):
x = inp
x = self.norm1(x)
x = self.conv1(x)
x = self.conv2(x)
x = self.sg(x)
x = x * self.sca(x)
x = self.conv3(x)
if self.drop_out_rate > 0:
x = self.dropout1(x)
y = inp + x * self.beta
x = self.conv4(self.norm2(y))
x = self.sg(x)
x = self.conv5(x)
if self.drop_out_rate > 0:
x = self.dropout2(x)
return y + x * self.gamma
NAFNet 整体模型代码如下:
class NAFNet(nn.Layer):
def __init__(self, img_channel=3, width=16, middle_blk_num=1, enc_blk_nums=[], dec_blk_nums=[]):
super().__init__()
self.intro = nn.Conv2D(in_channels=img_channel, out_channels=width, kernel_size=3, padding=1, stride=1,
groups=1,
bias_attr=True)
self.ending = nn.Conv2D(in_channels=width, out_channels=img_channel, kernel_size=3, padding=1, stride=1,
groups=1,
bias_attr=True)
self.encoders = nn.LayerList()
self.decoders = nn.LayerList()
self.middle_blks = nn.LayerList()
self.ups = nn.LayerList()
self.downs = nn.LayerList()
chan = width
for num in enc_blk_nums:
self.encoders.append(
nn.Sequential(
*[NAFBlock(chan) for _ in range(num)]
)
)
self.downs.append(
nn.Conv2D(chan, 2 * chan, 2, 2)
)
chan = chan * 2
self.middle_blks = \
nn.Sequential(
*[NAFBlock(chan) for _ in range(middle_blk_num)]
)
for num in dec_blk_nums:
self.ups.append(
nn.Sequential(
nn.Conv2D(chan, chan * 2, 1, bias_attr=False),
nn.PixelShuffle(2)
)
)
chan = chan // 2
self.decoders.append(
nn.Sequential(
*[NAFBlock(chan) for _ in range(num)]
)
)
self.padder_size = 2 ** len(self.encoders)
def forward(self, inp):
B, C, H, W = inp.shape
inp = self.check_image_size(inp)
x = self.intro(inp)
encs = []
for encoder, down in zip(self.encoders, self.downs):
x = encoder(x)
encs.append(x)
x = down(x)
x = self.middle_blks(x)
for decoder, up, enc_skip in zip(self.decoders, self.ups, encs[::-1]):
x = up(x)
x = x + enc_skip
x = decoder(x)
x = self.ending(x)
x = x + inp
return x[:, :, :H, :W]
def check_image_size(self, x):
_, _, h, w = x.shape
mod_pad_h = (self.padder_size - h % self.padder_size) % self.padder_size
mod_pad_w = (self.padder_size - w % self.padder_size) % self.padder_size
x = F.pad(x, [0, mod_pad_w, 0, mod_pad_h])
return x
ze - h % self.padder_size) % self.padder_size
mod_pad_w = (self.padder_size - w % self.padder_size) % self.padder_size
x = F.pad(x, [0, mod_pad_w, 0, mod_pad_h])
return x
2. 复现精度
在 SSID 测试集上测试,达到验收最低标准 PSNR: 40.20:
| NAFNet | PSNR | SSIM |
|---|---|---|
| Pytorch | 40.30 | 0.961 |
| Paddle | 40.23 | 0.959 |
注: 经过我们测试,8 卡跑完 40w 轮的 PSNR 是 40.2285.
3. 数据集、预训练模型、文件结构
3.1数据集:
训练和测试数据为 SIDD,其中训练数据大小为 512*512.
已经整理好的数据已放在了 Ai Studio 里.
使用以下命令解压数据:
# 解压
!cd data && unzip -oq -d SIDD_Data/ data149460/SIDD.zip
# 添加软链接
!cd work && ln -s ../data/SIDD_Data SIDD_Data
3.2 预训练模型
模型比较大,因此放在 AI Studio 里了,数据集中的 model_best.pdparams 即为复现得到的最优权重
3.3 文件结构
NAFNet-pd
|-- dataloaders
|-- SIDD_Data
|-- train # SIDD-Medium 训练数据
|-- val # SIDD 测试数据
|-- SIDD_patches
|-- train_mini # 小训练数据,用于TIPC测试
|-- val_mini # 小测试数据,用于TIPC测试
|-- logs # 训练日志
|-- test_tipc # TIPC: Linux GPU/CPU 基础训练推理测试
|-- networks
|-- NAFNet_arch.py # NAFNet模型代码
|-- utils # 一些工具代码
|-- config.py # 配置文件
|-- export_model.py # 预训练模型的导出代码
|-- infer.py # 模型推理代码
|-- LICENSE # LICENSE文件
|-- losses.py # 损失函数
|-- predict.py # 模型预测代码
|-- README.md # README.md文件
|-- sidd_data_preprocessing.py # SIDD数据预处理代码
|-- test_denoising_sidd.py # 测试SIDD数据上的指标
|-- train.py # TIPC训练测试代码
|-- train_denoising_1card.py # 单机单卡训练代码
|-- train_denoising_4cards.py # 单机多卡训练代码
|-- training_1card.yml # 单机单卡训练配置文件
|-- training_4cards.py # 单机多卡训练配置文件
4. 环境依赖
PaddlePaddle == 2.2.2, 若用 paddle_2.3.2 则 paddle.cumsum() 函数有问题,会带来错误的推理结果
scikit-image == 0.19.3
yacs == 0.1.8
natsort == 8.2.0
!pip install scikit-image yacs natsort
Looking in indexes: https://pypi.tuna.tsinghua.edu.cn/simple
Collecting scikit-image
Downloading https://pypi.tuna.tsinghua.edu.cn/packages/2d/ba/63ce953b7d593bd493e80be158f2d9f82936582380aee0998315510633aa/scikit_image-0.19.3-cp37-cp37m-manylinux_2_12_x86_64.manylinux2010_x86_64.whl (13.5 MB)
[2K [90m━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━[0m [32m13.5/13.5 MB[0m [31m1.0 MB/s[0m eta [36m0:00:00[0m00:01[0m00:01[0mm
[?25hCollecting yacs
Downloading https://pypi.tuna.tsinghua.edu.cn/packages/38/4f/fe9a4d472aa867878ce3bb7efb16654c5d63672b86dc0e6e953a67018433/yacs-0.1.8-py3-none-any.whl (14 kB)
Collecting natsort
Downloading https://pypi.tuna.tsinghua.edu.cn/packages/3e/58/61c4b4fd9e597affdcd3347d5991fa5be404af26f19932d3116b67e133da/natsort-8.2.0-py3-none-any.whl (37 kB)
Requirement already satisfied: networkx>=2.2 in /opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages (from scikit-image) (2.4)
Requirement already satisfied: scipy>=1.4.1 in /opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages (from scikit-image) (1.6.3)
Requirement already satisfied: imageio>=2.4.1 in /opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages (from scikit-image) (2.6.1)
Collecting tifffile>=2019.7.26
Downloading https://pypi.tuna.tsinghua.edu.cn/packages/d8/38/85ae5ed77598ca90558c17a2f79ddaba33173b31cf8d8f545d34d9134f0d/tifffile-2021.11.2-py3-none-any.whl (178 kB)
[2K [90m━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━[0m [32m178.9/178.9 kB[0m [31m2.2 MB/s[0m eta [36m0:00:00[0ma [36m0:00:01[0m
[?25hCollecting PyWavelets>=1.1.1
Downloading https://pypi.tuna.tsinghua.edu.cn/packages/ae/56/4441877073d8a5266dbf7b04c7f3dc66f1149c8efb9323e0ef987a9bb1ce/PyWavelets-1.3.0-cp37-cp37m-manylinux_2_5_x86_64.manylinux1_x86_64.manylinux_2_12_x86_64.manylinux2010_x86_64.whl (6.4 MB)
[2K [90m━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━[0m [32m6.4/6.4 MB[0m [31m2.4 MB/s[0m eta [36m0:00:00[0m00:01[0m00:01[0m
[?25hRequirement already satisfied: packaging>=20.0 in /opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages (from scikit-image) (21.3)
Requirement already satisfied: pillow!=7.1.0,!=7.1.1,!=8.3.0,>=6.1.0 in /opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages (from scikit-image) (7.1.2)
Requirement already satisfied: numpy>=1.17.0 in /opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages (from scikit-image) (1.20.3)
Requirement already satisfied: PyYAML in /opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages (from yacs) (5.1.2)
Requirement already satisfied: decorator>=4.3.0 in /opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages (from networkx>=2.2->scikit-image) (4.4.2)
Requirement already satisfied: pyparsing!=3.0.5,>=2.0.2 in /opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages (from packaging>=20.0->scikit-image) (3.0.9)
Installing collected packages: yacs, tifffile, PyWavelets, natsort, scikit-image
Successfully installed PyWavelets-1.3.0 natsort-8.2.0 scikit-image-0.19.3 tifffile-2021.11.2 yacs-0.1.8
[1m[[0m[34;49mnotice[0m[1;39;49m][0m[39;49m A new release of pip available: [0m[31;49m22.1.2[0m[39;49m -> [0m[32;49m22.3[0m
[1m[[0m[34;49mnotice[0m[1;39;49m][0m[39;49m To update, run: [0m[32;49mpip install --upgrade pip[0m
5. 快速开始
GPU数量改变时,须保证
total_batchsize*iter == 8gpus*8bs*400000iters
与官方保持一致
5.1 模型训练
为更好的体验,建议使用单机多卡训练,例如fork并运行脚本任务:
https://aistudio.baidu.com/aistudio/clusterprojectdetail/3792518
# 单机单卡
!cd work && python train_denoising_1card.py
/opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages/paddle/distributed/parallel.py:136: UserWarning: Currently not a parallel execution environment, `paddle.distributed.init_parallel_env` will not do anything.
"Currently not a parallel execution environment, `paddle.distributed.init_parallel_env` will not do anything."
1
W1020 19:01:40.903077 2034 device_context.cc:447] Please NOTE: device: 0, GPU Compute Capability: 7.0, Driver API Version: 11.2, Runtime API Version: 10.1
W1020 19:01:40.911723 2034 device_context.cc:465] device: 0, cuDNN Version: 7.6.
Evaluation after every 40000.0 Iterations !!!
Iter: 20 Time: 34.5868 Loss: 5.0979 LR: 0.000125
Iter: 40 Time: 66.5819 Loss: 0.6485 LR: 0.000125
Iter: 60 Time: 98.5737 Loss: -1.0570 LR: 0.000125
Iter: 80 Time: 130.5603 Loss: -6.1868 LR: 0.000125
Iter: 100 Time: 162.5479 Loss: -7.0057 LR: 0.000125
Iter: 120 Time: 194.5214 Loss: -11.3977 LR: 0.000125
Iter: 140 Time: 226.4824 Loss: -11.8900 LR: 0.000125
Iter: 160 Time: 258.4536 Loss: -8.5898 LR: 0.000125
Iter: 180 Time: 290.4267 Loss: -12.4031 LR: 0.000125
Iter: 200 Time: 322.3994 Loss: -14.6033 LR: 0.000125
Iter: 220 Time: 354.3700 Loss: -15.5492 LR: 0.000125
Iter: 240 Time: 386.3485 Loss: -18.7449 LR: 0.000125
Iter: 260 Time: 418.3124 Loss: -19.1128 LR: 0.000125
Iter: 280 Time: 450.2758 Loss: -18.4319 LR: 0.000125
Iter: 300 Time: 482.2334 Loss: -19.2498 LR: 0.000125
Iter: 320 Time: 514.1881 Loss: -19.4932 LR: 0.000125
Iter: 340 Time: 546.1351 Loss: -22.2910 LR: 0.000125
Iter: 360 Time: 578.0893 Loss: -21.6711 LR: 0.000125
Iter: 380 Time: 610.0461 Loss: -20.3410 LR: 0.000125
Iter: 400 Time: 641.9911 Loss: -16.5690 LR: 0.000125
Iter: 420 Time: 673.9471 Loss: -24.3729 LR: 0.000125
Iter: 440 Time: 705.9050 Loss: -21.5036 LR: 0.000125
Iter: 460 Time: 737.8757 Loss: -24.0739 LR: 0.000125
Iter: 480 Time: 769.8266 Loss: -23.0572 LR: 0.000125
Iter: 500 Time: 801.7718 Loss: -24.9329 LR: 0.000125
Iter: 520 Time: 833.7224 Loss: -24.4976 LR: 0.000125
Iter: 540 Time: 865.6621 Loss: -26.0905 LR: 0.000125
Iter: 560 Time: 897.6053 Loss: -24.2350 LR: 0.000125
Iter: 580 Time: 929.5543 Loss: -22.0951 LR: 0.000125
Iter: 600 Time: 961.5056 Loss: -25.6550 LR: 0.000125
Iter: 620 Time: 993.4508 Loss: -24.7059 LR: 0.000125
Iter: 640 Time: 1025.3989 Loss: -26.5059 LR: 0.000125
Iter: 660 Time: 1057.3417 Loss: -26.5044 LR: 0.000125
Iter: 680 Time: 1089.2906 Loss: -28.4881 LR: 0.000125
Iter: 700 Time: 1121.2376 Loss: -28.1797 LR: 0.000125
Iter: 720 Time: 1153.1795 Loss: -26.2520 LR: 0.000125
Iter: 740 Time: 1185.1209 Loss: -28.9906 LR: 0.000125
Iter: 760 Time: 1217.0699 Loss: -25.0321 LR: 0.000125
Iter: 780 Time: 1249.0127 Loss: -31.3646 LR: 0.000125
Iter: 800 Time: 1280.9706 Loss: -28.7375 LR: 0.000125
Iter: 820 Time: 1312.9116 Loss: -29.0214 LR: 0.000125
Iter: 840 Time: 1344.8571 Loss: -29.3821 LR: 0.000125
Iter: 860 Time: 1376.8067 Loss: -31.0492 LR: 0.000125
Iter: 880 Time: 1408.7478 Loss: -27.5379 LR: 0.000125
Iter: 900 Time: 1440.6903 Loss: -27.2364 LR: 0.000125
Iter: 920 Time: 1472.6369 Loss: -28.9533 LR: 0.000125
Iter: 940 Time: 1504.5947 Loss: -27.8460 LR: 0.000125
Iter: 960 Time: 1536.5525 Loss: -24.4605 LR: 0.000125
Iter: 980 Time: 1568.4962 Loss: -31.9323 LR: 0.000125
Iter: 1000 Time: 1600.4357 Loss: -28.4699 LR: 0.000125
Iter: 1020 Time: 1632.3832 Loss: -30.8814 LR: 0.000125
Iter: 1040 Time: 1664.3271 Loss: -30.9682 LR: 0.000125
Iter: 1060 Time: 1696.2796 Loss: -29.5606 LR: 0.000125
Iter: 1080 Time: 1728.2309 Loss: -31.2389 LR: 0.000125
Iter: 1100 Time: 1760.1906 Loss: -31.2284 LR: 0.000125
Iter: 1120 Time: 1792.1425 Loss: -30.8374 LR: 0.000125
Iter: 1140 Time: 1824.1003 Loss: -32.3375 LR: 0.000125
Iter: 1160 Time: 1856.0778 Loss: -34.0436 LR: 0.000125
Iter: 1180 Time: 1888.0189 Loss: -34.9844 LR: 0.000125
Iter: 1200 Time: 1919.9715 Loss: -32.2476 LR: 0.000125
Iter: 1220 Time: 1951.9151 Loss: -32.1040 LR: 0.000125
Iter: 1240 Time: 1983.8601 Loss: -33.2099 LR: 0.000125
Iter: 1260 Time: 2015.8078 Loss: -34.4656 LR: 0.000125
Iter: 1280 Time: 2047.7595 Loss: -32.5396 LR: 0.000125
Iter: 1300 Time: 2079.6991 Loss: -34.2393 LR: 0.000125
Iter: 1320 Time: 2111.6500 Loss: -31.3982 LR: 0.000125
Iter: 1340 Time: 2143.6109 Loss: -33.0328 LR: 0.000125
Iter: 1360 Time: 2175.5707 Loss: -29.4103 LR: 0.000125
Iter: 1380 Time: 2207.5318 Loss: -32.1473 LR: 0.000125
Iter: 1400 Time: 2239.4772 Loss: -30.8254 LR: 0.000125
Iter: 1420 Time: 2271.4253 Loss: -29.1734 LR: 0.000125
Iter: 1440 Time: 2303.3941 Loss: -31.9800 LR: 0.000125
Iter: 1460 Time: 2335.3471 Loss: -30.2023 LR: 0.000125
Iter: 1480 Time: 2367.2864 Loss: -31.3700 LR: 0.000125
Iter: 1500 Time: 2399.2500 Loss: -33.2391 LR: 0.000125
Iter: 1520 Time: 2431.2002 Loss: -29.2322 LR: 0.000125
Iter: 1540 Time: 2463.1749 Loss: -35.7182 LR: 0.000125
Iter: 1560 Time: 2495.1292 Loss: -33.0141 LR: 0.000125
Iter: 1580 Time: 2527.0843 Loss: -31.4256 LR: 0.000125
Iter: 1600 Time: 2559.0335 Loss: -32.6950 LR: 0.000125
Iter: 1620 Time: 2590.9871 Loss: -31.5490 LR: 0.000125
Iter: 1640 Time: 2622.9536 Loss: -31.7845 LR: 0.000125
Iter: 1660 Time: 2654.9168 Loss: -32.3535 LR: 0.000125
Iter: 1680 Time: 2686.8888 Loss: -32.3783 LR: 0.000125
Iter: 1700 Time: 2718.8597 Loss: -29.6367 LR: 0.000125
Iter: 1720 Time: 2750.8165 Loss: -34.7280 LR: 0.000125
Iter: 1740 Time: 2782.7651 Loss: -30.8653 LR: 0.000125
Iter: 1760 Time: 2814.7198 Loss: -32.8648 LR: 0.000125
Iter: 1780 Time: 2846.6687 Loss: -31.9529 LR: 0.000125
Iter: 1800 Time: 2878.6256 Loss: -33.4554 LR: 0.000125
Iter: 1820 Time: 2910.5731 Loss: -32.7492 LR: 0.000125
Iter: 1840 Time: 2942.5234 Loss: -32.4425 LR: 0.000125
Iter: 1860 Time: 2974.4790 Loss: -33.2847 LR: 0.000125
Iter: 1880 Time: 3006.4523 Loss: -33.7914 LR: 0.000125
Iter: 1900 Time: 3038.4083 Loss: -30.8973 LR: 0.000125
Iter: 1920 Time: 3070.3788 Loss: -33.4461 LR: 0.000125
Iter: 1940 Time: 3102.3347 Loss: -37.2922 LR: 0.000125
Iter: 1960 Time: 3134.2867 Loss: -36.3871 LR: 0.000125
Iter: 1980 Time: 3166.2456 Loss: -35.0707 LR: 0.000125
Iter: 2000 Time: 3198.1908 Loss: -35.0973 LR: 0.000125
Iter: 2020 Time: 3230.1362 Loss: -34.9464 LR: 0.000125
Iter: 2040 Time: 3262.0797 Loss: -36.5722 LR: 0.000125
Iter: 2060 Time: 3294.0431 Loss: -34.8382 LR: 0.000125
Iter: 2080 Time: 3325.9953 Loss: -33.7397 LR: 0.000125
Iter: 2100 Time: 3357.9643 Loss: -35.8226 LR: 0.000125
Iter: 2120 Time: 3389.9194 Loss: -29.5324 LR: 0.000125
Iter: 2140 Time: 3421.8822 Loss: -33.3482 LR: 0.000125
Iter: 2160 Time: 3453.8355 Loss: -32.3968 LR: 0.000125
Iter: 2180 Time: 3485.7914 Loss: -31.5354 LR: 0.000125
Iter: 2200 Time: 3517.7496 Loss: -34.8590 LR: 0.000125
Iter: 2220 Time: 3549.7074 Loss: -34.9754 LR: 0.000125
Iter: 2240 Time: 3581.6700 Loss: -34.9909 LR: 0.000125
Iter: 2260 Time: 3613.6387 Loss: -35.7742 LR: 0.000125
Iter: 2280 Time: 3645.6081 Loss: -32.8874 LR: 0.000125
Iter: 2300 Time: 3677.5807 Loss: -35.5190 LR: 0.000125
Iter: 2320 Time: 3709.5338 Loss: -31.0241 LR: 0.000125
Iter: 2340 Time: 3741.4945 Loss: -33.9211 LR: 0.000125
Iter: 2360 Time: 3773.4561 Loss: -30.7827 LR: 0.000125
Iter: 2380 Time: 3805.4124 Loss: -30.8279 LR: 0.000125
Iter: 2400 Time: 3837.3773 Loss: -34.3921 LR: 0.000125
Iter: 2420 Time: 3869.3516 Loss: -33.9188 LR: 0.000125
Iter: 2440 Time: 3901.3204 Loss: -33.6715 LR: 0.000125
Iter: 2460 Time: 3933.2933 Loss: -33.8992 LR: 0.000125
Iter: 2480 Time: 3965.2724 Loss: -35.8468 LR: 0.000125
Iter: 2500 Time: 3997.2404 Loss: -31.5401 LR: 0.000125
Iter: 2520 Time: 4029.1977 Loss: -36.2019 LR: 0.000125
Iter: 2540 Time: 4061.1579 Loss: -33.5530 LR: 0.000125
Iter: 2560 Time: 4093.1182 Loss: -35.9242 LR: 0.000125
Iter: 2580 Time: 4125.1135 Loss: -35.2729 LR: 0.000125
Iter: 2600 Time: 4157.0731 Loss: -35.7171 LR: 0.000125
Iter: 2620 Time: 4189.0358 Loss: -32.5176 LR: 0.000125
Iter: 2640 Time: 4220.9953 Loss: -35.0287 LR: 0.000125
Iter: 2660 Time: 4252.9694 Loss: -34.8886 LR: 0.000125
Iter: 2680 Time: 4284.9359 Loss: -36.1052 LR: 0.000125
Iter: 2700 Time: 4316.9050 Loss: -35.2262 LR: 0.000125
Iter: 2720 Time: 4348.8653 Loss: -35.5603 LR: 0.000125
Iter: 2740 Time: 4380.8220 Loss: -36.0780 LR: 0.000125
Iter: 2760 Time: 4412.7734 Loss: -34.3746 LR: 0.000125
Iter: 2780 Time: 4444.7318 Loss: -34.7280 LR: 0.000125
Iter: 2800 Time: 4476.6977 Loss: -37.5366 LR: 0.000125
Iter: 2820 Time: 4508.6643 Loss: -37.0568 LR: 0.000125
Iter: 2840 Time: 4540.6264 Loss: -32.6439 LR: 0.000125
Iter: 2860 Time: 4572.6036 Loss: -34.4370 LR: 0.000125
Iter: 2880 Time: 4604.5836 Loss: -34.3403 LR: 0.000125
Iter: 2900 Time: 4636.5485 Loss: -34.8989 LR: 0.000125
Iter: 2920 Time: 4668.5243 Loss: -35.5309 LR: 0.000125
Iter: 2940 Time: 4700.4910 Loss: -36.1856 LR: 0.000125
Iter: 2960 Time: 4732.4663 Loss: -35.2291 LR: 0.000125
Iter: 2980 Time: 4764.4312 Loss: -36.8557 LR: 0.000125
Iter: 3000 Time: 4796.4031 Loss: -35.9209 LR: 0.000125
Iter: 3020 Time: 4828.3986 Loss: -33.7851 LR: 0.000125
Iter: 3040 Time: 4860.3935 Loss: -34.5691 LR: 0.000125
Iter: 3060 Time: 4892.3808 Loss: -33.5804 LR: 0.000125
Iter: 3080 Time: 4924.3494 Loss: -34.2071 LR: 0.000125
Iter: 3100 Time: 4956.3097 Loss: -34.3836 LR: 0.000125
Iter: 3120 Time: 4988.2732 Loss: -32.8416 LR: 0.000125
Iter: 3140 Time: 5020.2300 Loss: -36.3290 LR: 0.000125
Iter: 3160 Time: 5052.1893 Loss: -35.6801 LR: 0.000125
Iter: 3180 Time: 5084.1557 Loss: -37.0207 LR: 0.000125
Iter: 3200 Time: 5116.1246 Loss: -35.1333 LR: 0.000125
Iter: 3220 Time: 5148.1013 Loss: -36.2978 LR: 0.000125
Iter: 3240 Time: 5180.0767 Loss: -35.8655 LR: 0.000125
Iter: 3260 Time: 5212.0472 Loss: -34.3651 LR: 0.000125
Iter: 3280 Time: 5244.0104 Loss: -36.1770 LR: 0.000125
Iter: 3300 Time: 5275.9754 Loss: -38.5231 LR: 0.000125
Iter: 3320 Time: 5307.9377 Loss: -35.1442 LR: 0.000125
Iter: 3340 Time: 5339.8862 Loss: -37.3816 LR: 0.000125
Iter: 3360 Time: 5371.8457 Loss: -36.2682 LR: 0.000125
Iter: 3380 Time: 5403.8106 Loss: -34.6979 LR: 0.000125
Iter: 3400 Time: 5435.7813 Loss: -35.9078 LR: 0.000125
Iter: 3420 Time: 5467.7520 Loss: -34.1758 LR: 0.000125
Iter: 3440 Time: 5499.7232 Loss: -37.4560 LR: 0.000125
Iter: 3460 Time: 5531.6937 Loss: -35.8099 LR: 0.000125
Iter: 3480 Time: 5563.6557 Loss: -36.0352 LR: 0.000125
Iter: 3500 Time: 5595.6166 Loss: -35.3332 LR: 0.000125
Iter: 3520 Time: 5627.5867 Loss: -37.3237 LR: 0.000125
Iter: 3540 Time: 5659.5487 Loss: -38.2850 LR: 0.000125
Iter: 3560 Time: 5691.5225 Loss: -36.1598 LR: 0.000125
Iter: 3580 Time: 5723.5000 Loss: -34.6900 LR: 0.000125
Iter: 3600 Time: 5755.4814 Loss: -37.5566 LR: 0.000125
Iter: 3620 Time: 5787.4466 Loss: -33.7685 LR: 0.000125
Iter: 3640 Time: 5819.4109 Loss: -35.4327 LR: 0.000125
Iter: 3660 Time: 5851.3882 Loss: -34.7380 LR: 0.000125
Iter: 3680 Time: 5883.3863 Loss: -35.4435 LR: 0.000125
Iter: 3700 Time: 5915.3531 Loss: -33.7013 LR: 0.000125
Iter: 3720 Time: 5947.3219 Loss: -38.2070 LR: 0.000125
Iter: 3740 Time: 5979.2912 Loss: -32.1783 LR: 0.000125
Iter: 3760 Time: 6011.2631 Loss: -34.3979 LR: 0.000125
Iter: 3780 Time: 6043.2227 Loss: -37.2344 LR: 0.000125
Iter: 3800 Time: 6075.1820 Loss: -36.0525 LR: 0.000125
Iter: 3820 Time: 6107.1450 Loss: -31.6544 LR: 0.000125
Iter: 3840 Time: 6139.1068 Loss: -36.0038 LR: 0.000125
Iter: 3860 Time: 6171.0745 Loss: -36.8350 LR: 0.000125
Iter: 3880 Time: 6203.0329 Loss: -37.2674 LR: 0.000125
Iter: 3900 Time: 6235.0078 Loss: -37.3040 LR: 0.000125
Iter: 3920 Time: 6266.9828 Loss: -35.3462 LR: 0.000125
Iter: 3940 Time: 6298.9578 Loss: -35.1283 LR: 0.000125
Iter: 3960 Time: 6330.9216 Loss: -35.1235 LR: 0.000125
Iter: 3980 Time: 6362.8894 Loss: -36.6551 LR: 0.000125
Iter: 4000 Time: 6394.8530 Loss: -34.0495 LR: 0.000125
Iter: 4020 Time: 6426.8114 Loss: -36.9395 LR: 0.000125
Iter: 4040 Time: 6458.7660 Loss: -33.3941 LR: 0.000125
Iter: 4060 Time: 6490.7220 Loss: -37.6647 LR: 0.000125
Iter: 4080 Time: 6522.6812 Loss: -34.4313 LR: 0.000125
Iter: 4100 Time: 6554.6433 Loss: -33.9213 LR: 0.000125
Iter: 4120 Time: 6586.6072 Loss: -36.7969 LR: 0.000125
Iter: 4140 Time: 6618.5791 Loss: -34.5149 LR: 0.000125
Iter: 4160 Time: 6650.5614 Loss: -38.9674 LR: 0.000125
Iter: 4180 Time: 6682.5493 Loss: -35.1121 LR: 0.000125
Iter: 4200 Time: 6714.5150 Loss: -35.9254 LR: 0.000125
Iter: 4220 Time: 6746.4857 Loss: -35.0480 LR: 0.000125
Iter: 4240 Time: 6778.4606 Loss: -34.3342 LR: 0.000125
Iter: 4260 Time: 6810.4344 Loss: -35.7448 LR: 0.000125
Iter: 4280 Time: 6842.4096 Loss: -35.1190 LR: 0.000125
Iter: 4300 Time: 6874.3812 Loss: -36.2833 LR: 0.000125
Iter: 4320 Time: 6906.3573 Loss: -35.4242 LR: 0.000125
Iter: 4340 Time: 6938.3289 Loss: -37.1446 LR: 0.000125
Iter: 4360 Time: 6970.3003 Loss: -38.0218 LR: 0.000125
Iter: 4380 Time: 7002.2673 Loss: -36.0445 LR: 0.000125
Iter: 4400 Time: 7034.2426 Loss: -33.6088 LR: 0.000125
Iter: 4420 Time: 7066.2176 Loss: -32.2386 LR: 0.000125
Iter: 4440 Time: 7098.1799 Loss: -35.3044 LR: 0.000125
Iter: 4460 Time: 7130.1363 Loss: -34.2444 LR: 0.000125
Iter: 4480 Time: 7162.1118 Loss: -35.9526 LR: 0.000125
Iter: 4500 Time: 7194.0995 Loss: -34.0002 LR: 0.000125
Iter: 4520 Time: 7226.0923 Loss: -36.5200 LR: 0.000125
Iter: 4540 Time: 7258.1420 Loss: -37.1925 LR: 0.000125
Iter: 4560 Time: 7290.1512 Loss: -37.5862 LR: 0.000125
Iter: 4580 Time: 7322.1713 Loss: -35.1697 LR: 0.000125
Iter: 4600 Time: 7354.1831 Loss: -38.5021 LR: 0.000125
Iter: 4620 Time: 7386.1946 Loss: -33.5170 LR: 0.000125
Iter: 4640 Time: 7418.2104 Loss: -36.2704 LR: 0.000125
Iter: 4660 Time: 7450.2200 Loss: -34.2640 LR: 0.000125
Iter: 4680 Time: 7482.2317 Loss: -35.8445 LR: 0.000125
Iter: 4700 Time: 7514.2480 Loss: -36.9070 LR: 0.000125
Iter: 4720 Time: 7546.2635 Loss: -36.9851 LR: 0.000125
Iter: 4740 Time: 7578.2900 Loss: -36.1501 LR: 0.000125
Iter: 4760 Time: 7610.3059 Loss: -36.8881 LR: 0.000125
Iter: 4780 Time: 7642.3295 Loss: -36.5769 LR: 0.000125
Iter: 4800 Time: 7674.3542 Loss: -33.5602 LR: 0.000125
Iter: 4820 Time: 7706.3678 Loss: -34.8755 LR: 0.000125
Iter: 4840 Time: 7738.3870 Loss: -37.7057 LR: 0.000125
Iter: 4860 Time: 7770.4066 Loss: -35.7606 LR: 0.000125
Iter: 4880 Time: 7802.4349 Loss: -36.9175 LR: 0.000125
Iter: 4900 Time: 7834.4521 Loss: -37.0523 LR: 0.000125
Iter: 4920 Time: 7866.4764 Loss: -36.1358 LR: 0.000125
Iter: 4940 Time: 7898.4860 Loss: -37.0530 LR: 0.000125
Iter: 4960 Time: 7930.5036 Loss: -34.8046 LR: 0.000125
Iter: 4980 Time: 7962.5145 Loss: -36.2263 LR: 0.000125
Iter: 5000 Time: 7994.5231 Loss: -38.0180 LR: 0.000125
Iter: 5020 Time: 8026.5396 Loss: -36.7718 LR: 0.000125
Iter: 5040 Time: 8058.5476 Loss: -38.9403 LR: 0.000125
Iter: 5060 Time: 8090.5783 Loss: -34.8355 LR: 0.000125
Iter: 5080 Time: 8122.5983 Loss: -35.0924 LR: 0.000125
Iter: 5100 Time: 8154.6215 Loss: -36.7193 LR: 0.000125
Iter: 5120 Time: 8186.6343 Loss: -35.4713 LR: 0.000125
Iter: 5140 Time: 8218.6509 Loss: -34.8370 LR: 0.000125
Iter: 5160 Time: 8250.6542 Loss: -37.9277 LR: 0.000125
Iter: 5180 Time: 8282.6622 Loss: -37.4167 LR: 0.000125
Iter: 5200 Time: 8314.6694 Loss: -34.4808 LR: 0.000125
Iter: 5220 Time: 8346.6898 Loss: -37.3901 LR: 0.000125
Iter: 5240 Time: 8378.7106 Loss: -34.6296 LR: 0.000125
Iter: 5260 Time: 8410.7324 Loss: -37.9288 LR: 0.000125
Iter: 5280 Time: 8442.7425 Loss: -36.9091 LR: 0.000125
Iter: 5300 Time: 8474.7679 Loss: -37.8298 LR: 0.000125
Iter: 5320 Time: 8506.7909 Loss: -33.7292 LR: 0.000125
Iter: 5340 Time: 8538.8197 Loss: -37.8354 LR: 0.000125
Iter: 5360 Time: 8570.8308 Loss: -37.1170 LR: 0.000125
Iter: 5380 Time: 8602.8424 Loss: -35.1707 LR: 0.000125
Iter: 5400 Time: 8634.8495 Loss: -36.3743 LR: 0.000125
Iter: 5420 Time: 8666.8621 Loss: -37.5056 LR: 0.000125
Iter: 5440 Time: 8698.8870 Loss: -38.8227 LR: 0.000125
Iter: 5460 Time: 8730.8986 Loss: -38.5384 LR: 0.000125
Iter: 5480 Time: 8762.9218 Loss: -35.0464 LR: 0.000125
Iter: 5500 Time: 8794.9365 Loss: -38.9008 LR: 0.000125
Iter: 5520 Time: 8826.9463 Loss: -36.6002 LR: 0.000125
Iter: 5540 Time: 8858.9533 Loss: -35.3303 LR: 0.000125
Iter: 5560 Time: 8890.9652 Loss: -36.0204 LR: 0.000125
Iter: 5580 Time: 8922.9789 Loss: -35.2732 LR: 0.000125
Iter: 5600 Time: 8955.0027 Loss: -36.7229 LR: 0.000125
Iter: 5620 Time: 8987.0338 Loss: -36.3978 LR: 0.000125
Iter: 5640 Time: 9019.0539 Loss: -38.4452 LR: 0.000125
Iter: 5660 Time: 9051.0863 Loss: -36.4200 LR: 0.000125
Iter: 5680 Time: 9083.1001 Loss: -37.0472 LR: 0.000125
Iter: 5700 Time: 9115.1128 Loss: -36.2071 LR: 0.000125
Iter: 5720 Time: 9147.1300 Loss: -37.0482 LR: 0.000125
Iter: 5740 Time: 9179.1578 Loss: -39.0609 LR: 0.000125
Iter: 5760 Time: 9211.1690 Loss: -38.4786 LR: 0.000125
Iter: 5780 Time: 9243.1910 Loss: -39.0149 LR: 0.000125
Iter: 5800 Time: 9275.2145 Loss: -38.4347 LR: 0.000125
Iter: 5820 Time: 9307.2358 Loss: -37.4505 LR: 0.000125
Iter: 5840 Time: 9339.2495 Loss: -37.8586 LR: 0.000125
Iter: 5860 Time: 9371.2625 Loss: -38.7746 LR: 0.000125
Iter: 5880 Time: 9403.2747 Loss: -36.7047 LR: 0.000125
Iter: 5900 Time: 9435.2891 Loss: -35.3562 LR: 0.000125
Iter: 5920 Time: 9467.3082 Loss: -39.1778 LR: 0.000125
Iter: 5940 Time: 9499.3206 Loss: -38.4955 LR: 0.000125
Iter: 5960 Time: 9531.3225 Loss: -39.5524 LR: 0.000125
Iter: 5980 Time: 9563.3328 Loss: -37.9607 LR: 0.000125
Iter: 6000 Time: 9595.3434 Loss: -36.6005 LR: 0.000125
Iter: 6020 Time: 9627.3469 Loss: -36.8303 LR: 0.000125
Iter: 6040 Time: 9659.3685 Loss: -37.3467 LR: 0.000125
Iter: 6060 Time: 9691.3845 Loss: -32.9066 LR: 0.000125
Iter: 6080 Time: 9723.4069 Loss: -37.5554 LR: 0.000125
Iter: 6100 Time: 9755.4186 Loss: -38.2732 LR: 0.000125
Iter: 6120 Time: 9787.4299 Loss: -36.3643 LR: 0.000125
Iter: 6140 Time: 9819.4422 Loss: -37.5204 LR: 0.000125
Iter: 6160 Time: 9851.4613 Loss: -35.6269 LR: 0.000125
Iter: 6180 Time: 9883.4830 Loss: -39.5719 LR: 0.000125
Iter: 6200 Time: 9915.4981 Loss: -39.3517 LR: 0.000125
Iter: 6220 Time: 9947.5215 Loss: -38.6832 LR: 0.000125
Iter: 6240 Time: 9979.5328 Loss: -39.0020 LR: 0.000125
Iter: 6260 Time: 10011.5518 Loss: -34.2150 LR: 0.000125
Iter: 6280 Time: 10043.5631 Loss: -38.0983 LR: 0.000125
Iter: 6300 Time: 10075.5961 Loss: -38.0267 LR: 0.000125
Iter: 6320 Time: 10107.6028 Loss: -36.7388 LR: 0.000125
Iter: 6340 Time: 10139.6117 Loss: -36.7122 LR: 0.000125
Iter: 6360 Time: 10171.6201 Loss: -39.1232 LR: 0.000125
Iter: 6380 Time: 10203.6373 Loss: -37.7977 LR: 0.000125
Iter: 6400 Time: 10235.6475 Loss: -36.9192 LR: 0.000125
Iter: 6420 Time: 10267.6690 Loss: -36.4063 LR: 0.000125
Iter: 6440 Time: 10299.6824 Loss: -37.3997 LR: 0.000125
Iter: 6460 Time: 10331.6903 Loss: -36.8655 LR: 0.000125
Iter: 6480 Time: 10363.7033 Loss: -38.2897 LR: 0.000125
Iter: 6500 Time: 10395.7179 Loss: -35.3241 LR: 0.000125
Iter: 6520 Time: 10427.7242 Loss: -37.1691 LR: 0.000125
Iter: 6540 Time: 10459.7336 Loss: -36.9672 LR: 0.000125
Iter: 6560 Time: 10491.7564 Loss: -37.5404 LR: 0.000125
Iter: 6580 Time: 10523.7725 Loss: -36.5347 LR: 0.000125
Iter: 6600 Time: 10555.8003 Loss: -37.5183 LR: 0.000125
Iter: 6620 Time: 10587.8140 Loss: -38.1343 LR: 0.000125
Iter: 6640 Time: 10619.8299 Loss: -39.2698 LR: 0.000125
Iter: 6660 Time: 10651.8438 Loss: -38.0983 LR: 0.000125
Iter: 6680 Time: 10683.8574 Loss: -37.9064 LR: 0.000125
Iter: 6700 Time: 10715.8686 Loss: -38.6463 LR: 0.000125
Iter: 6720 Time: 10747.8883 Loss: -35.1097 LR: 0.000125
Iter: 6740 Time: 10779.9161 Loss: -39.4870 LR: 0.000125
Iter: 6760 Time: 10811.9338 Loss: -38.9284 LR: 0.000125
Iter: 6780 Time: 10843.9438 Loss: -37.9355 LR: 0.000125
Iter: 6800 Time: 10875.9593 Loss: -35.8483 LR: 0.000125
Iter: 6820 Time: 10907.9806 Loss: -36.8394 LR: 0.000125
Iter: 6840 Time: 10939.9926 Loss: -39.5615 LR: 0.000125
Iter: 6860 Time: 10972.0114 Loss: -37.5685 LR: 0.000125
Iter: 6880 Time: 11004.0329 Loss: -38.6723 LR: 0.000125
Iter: 6900 Time: 11036.0504 Loss: -39.4202 LR: 0.000125
Iter: 6920 Time: 11068.0615 Loss: -37.7990 LR: 0.000125
Iter: 6940 Time: 11100.0815 Loss: -39.5928 LR: 0.000125
Iter: 6960 Time: 11132.0965 Loss: -39.1091 LR: 0.000125
Iter: 6980 Time: 11164.1326 Loss: -37.8166 LR: 0.000125
Iter: 7000 Time: 11196.1505 Loss: -38.1768 LR: 0.000125
Iter: 7020 Time: 11228.1689 Loss: -35.5331 LR: 0.000125
Iter: 7040 Time: 11260.1890 Loss: -39.9690 LR: 0.000125
Iter: 7060 Time: 11292.2126 Loss: -39.7653 LR: 0.000125
Iter: 7080 Time: 11324.2316 Loss: -38.2931 LR: 0.000125
Iter: 7100 Time: 11356.2500 Loss: -36.9157 LR: 0.000125
Iter: 7120 Time: 11388.2800 Loss: -38.6837 LR: 0.000125
Iter: 7140 Time: 11420.3057 Loss: -39.1057 LR: 0.000125
Iter: 7160 Time: 11452.3360 Loss: -38.6236 LR: 0.000125
Iter: 7180 Time: 11484.3427 Loss: -35.8251 LR: 0.000125
Iter: 7200 Time: 11516.3648 Loss: -36.1269 LR: 0.000125
Iter: 7220 Time: 11548.3808 Loss: -36.2580 LR: 0.000125
Iter: 7240 Time: 11580.3999 Loss: -39.1127 LR: 0.000125
Iter: 7260 Time: 11612.4101 Loss: -36.7831 LR: 0.000125
Iter: 7280 Time: 11644.4308 Loss: -37.4672 LR: 0.000125
Iter: 7300 Time: 11676.4720 Loss: -37.3497 LR: 0.000125
Iter: 7320 Time: 11708.4964 Loss: -38.9371 LR: 0.000125
Iter: 7340 Time: 11740.5115 Loss: -34.5199 LR: 0.000125
Iter: 7360 Time: 11772.5312 Loss: -38.7334 LR: 0.000125
Iter: 7380 Time: 11804.5478 Loss: -36.8170 LR: 0.000125
Iter: 7400 Time: 11836.5615 Loss: -37.9418 LR: 0.000125
Iter: 7420 Time: 11868.5847 Loss: -37.9877 LR: 0.000125
Iter: 7440 Time: 11900.6029 Loss: -39.2878 LR: 0.000125
Iter: 7460 Time: 11932.6289 Loss: -38.5154 LR: 0.000125
Iter: 7480 Time: 11964.6507 Loss: -37.7210 LR: 0.000125
Iter: 7500 Time: 11996.6666 Loss: -40.7244 LR: 0.000125
Iter: 7520 Time: 12028.7009 Loss: -38.6769 LR: 0.000125
Iter: 7540 Time: 12060.7251 Loss: -38.7526 LR: 0.000125
Iter: 7560 Time: 12092.7426 Loss: -39.7077 LR: 0.000125
Iter: 7580 Time: 12124.7552 Loss: -38.7930 LR: 0.000125
Iter: 7600 Time: 12156.7608 Loss: -38.4072 LR: 0.000125
Iter: 7620 Time: 12188.7869 Loss: -40.5515 LR: 0.000125
Iter: 7640 Time: 12220.7995 Loss: -37.4896 LR: 0.000125
Iter: 7660 Time: 12252.8127 Loss: -35.9185 LR: 0.000125
Iter: 7680 Time: 12284.8268 Loss: -38.6118 LR: 0.000125
^C
Traceback (most recent call last):
File "train_denoising_1card.py", line 185, in <module>
main()
File "train_denoising_1card.py", line 131, in main
l_total.backward()
File "<decorator-gen-128>", line 2, in backward
File "/opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages/paddle/fluid/wrapped_decorator.py", line 25, in __impl__
return wrapped_func(*args, **kwargs)
File "/opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages/paddle/fluid/framework.py", line 229, in __impl__
return func(*args, **kwargs)
File "/opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages/paddle/fluid/dygraph/varbase_patch_methods.py", line 249, in backward
framework._dygraph_tracer())
OSError: (External) KeyboardInterrupt:
At:
/opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages/paddle/autograd/py_layer.py(178): backward
/opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages/paddle/fluid/dygraph/varbase_patch_methods.py(249): backward
/opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages/paddle/fluid/framework.py(229): __impl__
/opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages/paddle/fluid/wrapped_decorator.py(25): __impl__
<decorator-gen-128>(2): backward
train_denoising_1card.py(131): main
train_denoising_1card.py(185): <module>
(at /paddle/paddle/fluid/imperative/basic_engine.cc:578)
# 单机四卡
# !cd work && python -m paddle.distributed.launch train_denoising_4cards.py
此处为用四张卡,配置文件为 training_4cards.yml.
由于训练模型采用的是脚本任务训练,本身脚本任务就有相应的日志记录,均保存在了 work/logs 文件夹下
5.2 模型评估
在 SIDD 测试数据上作测试
!cd work && python test_denoising_sidd.py --weight ../data/data168981/model_best.pdparams
W1020 22:27:01.528301 27132 device_context.cc:447] Please NOTE: device: 0, GPU Compute Capability: 7.0, Driver API Version: 11.2, Runtime API Version: 10.1
W1020 22:27:01.533494 27132 device_context.cc:465] device: 0, cuDNN Version: 7.6.
/opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages/paddle/framework/io.py:415: DeprecationWarning: Using or importing the ABCs from 'collections' instead of from 'collections.abc' is deprecated, and in 3.8 it will stop working
if isinstance(obj, collections.Iterable) and not isinstance(obj, (
Evaluation Start
100%|█████████████████████████████████████████| 160/160 [01:24<00:00, 1.90it/s]
Evaluation End
PSNR: 40.2024
SSIM: 0.9590
输出如下:
PSNR: 40.2024
SSIM: 0.9590
5.3模型预测
在 SIDD 小验证集上作预测,结果存放在 results/ 文件夹下
!cd work/ && python predict.py --model_ckpt ../data/data168981/model_best.pdparams --data_path ./SIDD_patches/val_mini/ --save_path results/ --save_images
Loading model ...
W1020 22:30:33.832536 27680 device_context.cc:447] Please NOTE: device: 0, GPU Compute Capability: 7.0, Driver API Version: 11.2, Runtime API Version: 10.1
W1020 22:30:33.839141 27680 device_context.cc:465] device: 0, cuDNN Version: 7.6.
/opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages/paddle/framework/io.py:415: DeprecationWarning: Using or importing the ABCs from 'collections' instead of from 'collections.abc' is deprecated, and in 3.8 it will stop working
if isinstance(obj, collections.Iterable) and not isinstance(obj, (
Loading data info ...
PSNR on test data 40.7486, SSIM on test data 0.9809,
输出结果如下:
PSNR on test data 40.7486, SSIM on test data 0.9809
5.4 单张图像去噪测试
导入单张图像,测试去噪效果,首先需要在work/test_images里上传一张图片.
# 先上传一张图片
import os.path as osp
from IPython.display import display
from PIL import Image
img_path = 'bird.png' # 改成自己上传的图片名称
full_img_path = osp.join(osp.abspath('work/test_images/'), img_path)
img = Image.open(full_img_path).convert('RGB')
print('以下为上传的图片:')
display(img)
以下为上传的图片:

需要指定干净图像和噪声图像,可以只给一张噪声图片,也可以只给一张干净图片,也可以都给.
-
给定一张噪声图片:指定参数
noisy_img,直接输出去噪图片. -
给定一张干净图片:指定参数
clean_img和noisyL,后者为噪声水平,默认为10,输出加噪图片和去噪图片. -
给定噪声图片和干净图片:直接输出去噪图片.
# 仅给定干净图片,噪声水平为10
!cd work && python predict_single.py --clean_img $full_img_path --save_images --noisyL 10 --model_path ../data/data168981/model_latest.pdparams
loading model from ../data/data168981/model_latest.pdparams
W1020 22:30:48.367162 27739 device_context.cc:447] Please NOTE: device: 0, GPU Compute Capability: 7.0, Driver API Version: 11.2, Runtime API Version: 10.1
W1020 22:30:48.372390 27739 device_context.cc:465] device: 0, cuDNN Version: 7.6.
/opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages/paddle/framework/io.py:415: DeprecationWarning: Using or importing the ABCs from 'collections' instead of from 'collections.abc' is deprecated, and in 3.8 it will stop working
if isinstance(obj, collections.Iterable) and not isinstance(obj, (
only clean image provided, noise level is 10
PSNR on test data 30.9145, SSIM on test data 0.9600
# 去噪效果查看
import glob
from IPython.display import display
from PIL import Image
imgs = glob.glob('work/test_images/*')
for path in imgs:
print(path)
img = Image.open(path)
display(img)
work/test_images/bird_noised.png

work/test_images/bird.png

work/test_images/bird_denoised.png

6. 复现心得
我又双叒叕来参加复现赛了!
NAFNet是在打百度网盘模糊文档修复时使用的网络,结果在兴智杯论文复现赛也出现了,便训练了SIDD去噪模型。
特别感谢不爱做科研的KeyK的协助~比心!
最后也特别感谢飞桨团队在复现过程中提供的帮助!
7. 关于作者
作者是来自中国地质大学(武汉)的在读研究生——方块;
个人项目:
此文章为搬运
原项目链接























 1555
1555

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








