5.参数估计——点估计与区间估计概念，置信区间的公式求法与Python实现求出结果

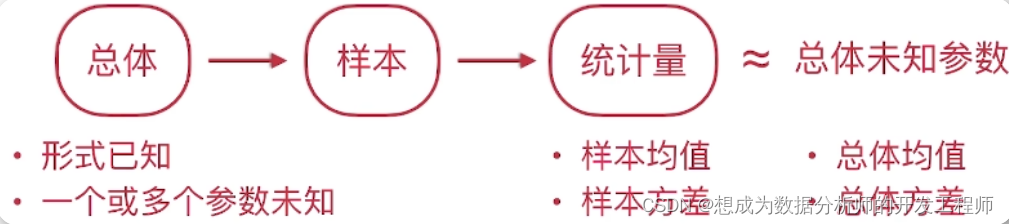
1.点估计

什么是点估计
设总体X的分布形式已知，但它的一个或多个参数未知，借助于总体X的一个样本来估计总体未知参数的值的问题称为参数的点估计问题

注意：

点估计的问题就是要构造一个适当的统计量（估计量），用它的观察值作为未知参数的近似值（估计值）
估计量的评选标准

• 无偏性
  若估计量的数学期望存在，并且该期望等于总体参数，则称为无偏估计
  无偏估计的实际意义就是："E(估计值) - 真值"的结果为0
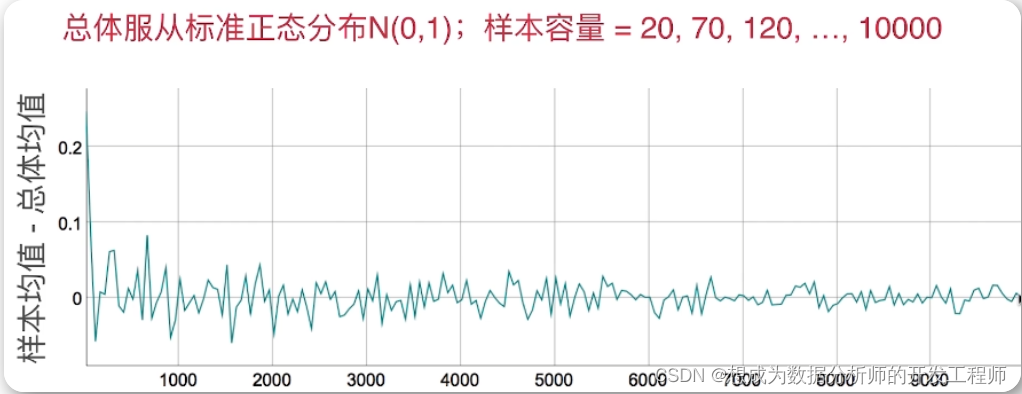
  不论总体服从什么分布，样本均值是总体均值的无偏估计；样本方差是总体方差的无偏估计

• 有效性
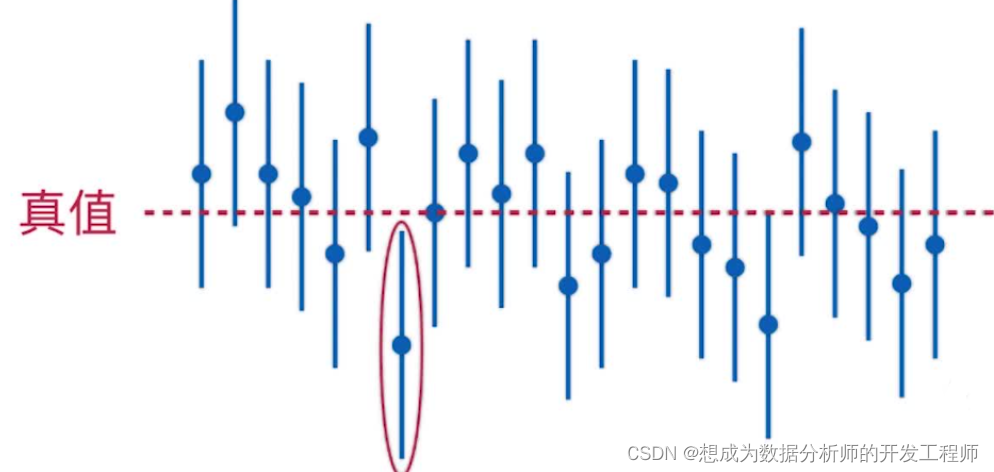
  有两个无偏估计θ₁和θ₂,如果在样本容量n相同的情况下，θ₁比θ₂更密集在真值附近，就认为θ₁比θ₂更理想换言之，无偏估计以方差最小者为好
• 相合性
  随着样本容量的增大，一个估计量的值稳定于待估参数的真值。满足此条件的估计量为相合估计量

2.区间估计

对于未知参数，我们不仅要得到近似值（点估计），还希望估计出一个范围（区间），并希望知道这个范围包含参数真值的可信程度。这种形式的估计称为区间估计，这样的区间称为置信区间
置信区间、置信水平
设(X₁,…,X_n)是取自总体X的一个样本，对于未知参数θ，给定α，0<α<1,如果存在统计量θ₁(X₁,…,X_n)，θ₂(X1,…,Xn)，使得P(θ1(X1,…,Xn)≤θ≤θ2(X1,…,Xn))≥1−α
那么，称[θ₁,θ₂]为θ的双侧1-α置信区间；称1-α为置信水平（也称作置信度或置信系数）。
注意：

对于置信区间和置信水平的理解：

• 固定样本容量n,若反复抽样多次，每个样本值确定一个区间，每个这样的区间要么包含θ的真值，要么不包含θ的真值
• 在这么多区间中，包含真值的约占100(1-α)%，不包含真值的占100α%
• 计算得到的区间属于那些包含真值的区间的可信程度为100(1-α)%，或“该区间包含真值”这一陈述的可信程度为100(1-α)%

3.求置信区间的步骤

较优的点估计应该属于置信区间，这是求置信区间的起始和基本思想

求未知参数的置信区间的步骤：

1. 寻求一个样本X₁,X₂,…X_n和一个统计量W(X₁,X₂,…X_n;θ)，使统计量W的分布不依赖于θ和其他未知参数，统计量W的构造，通常可以从θ的点估计着手
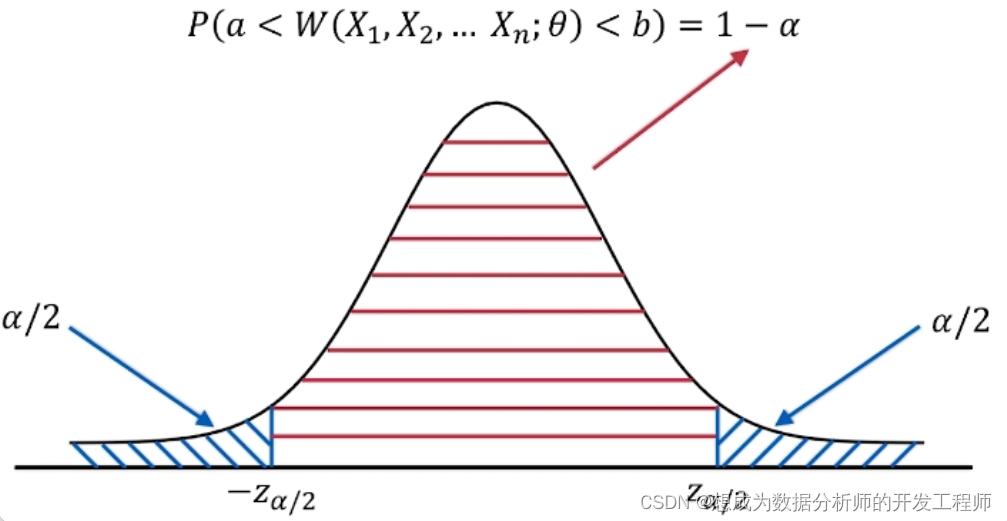
2. 对于给定的置信水平1-α，定出两个常数a和b，使得P(a < W(X₁,X₂,…X_n;θ) < b) = 1-α
3. 求解出θ的不等式θ₁ < θ < θ₂，则(θ₁,θ₂)为θ的一个置信水平为1-α的置信区间

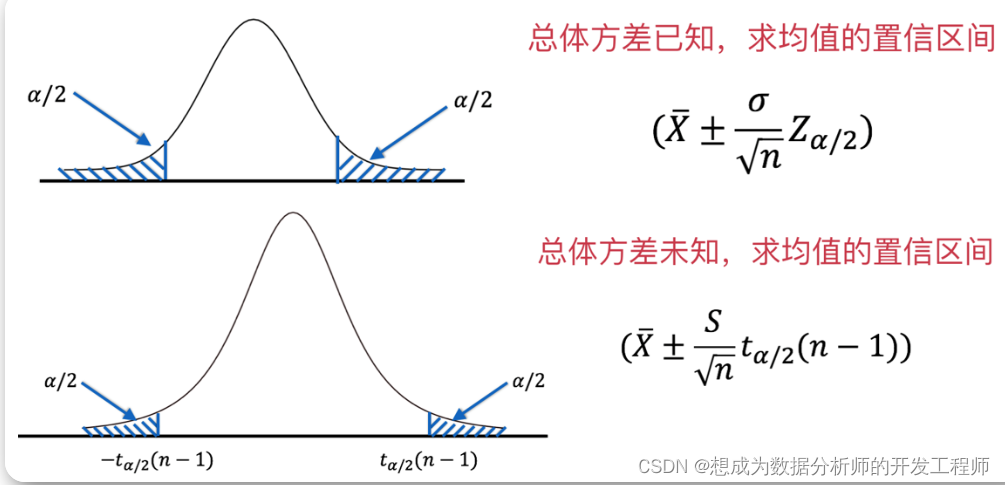
4.正态总体均值的置信区间（方差已知）

已知：总体X服从正态分布，且总体方差已知

求：均值的置信区间

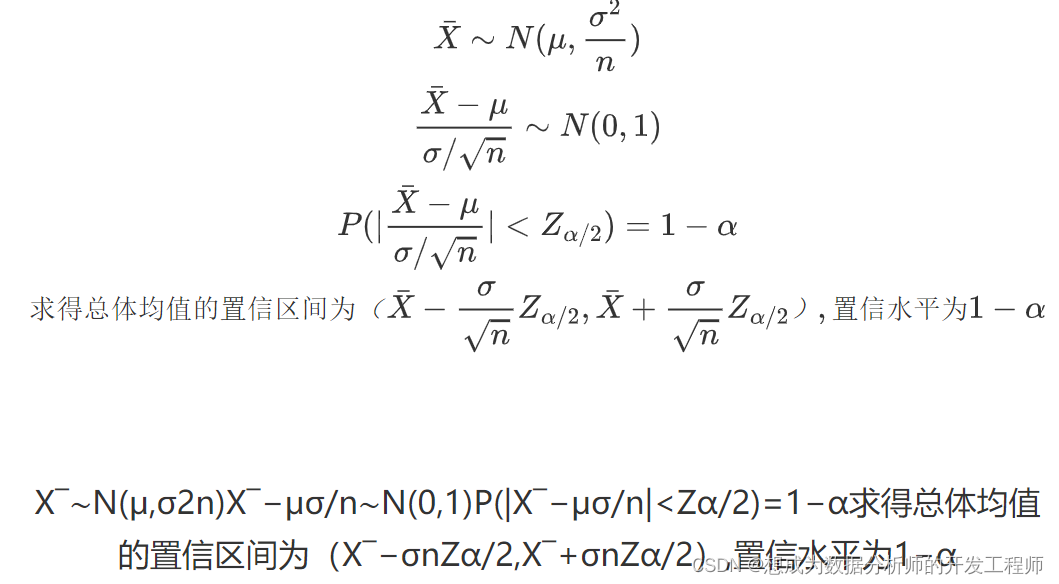
5.正态总体均值的置信区间(方差未知)

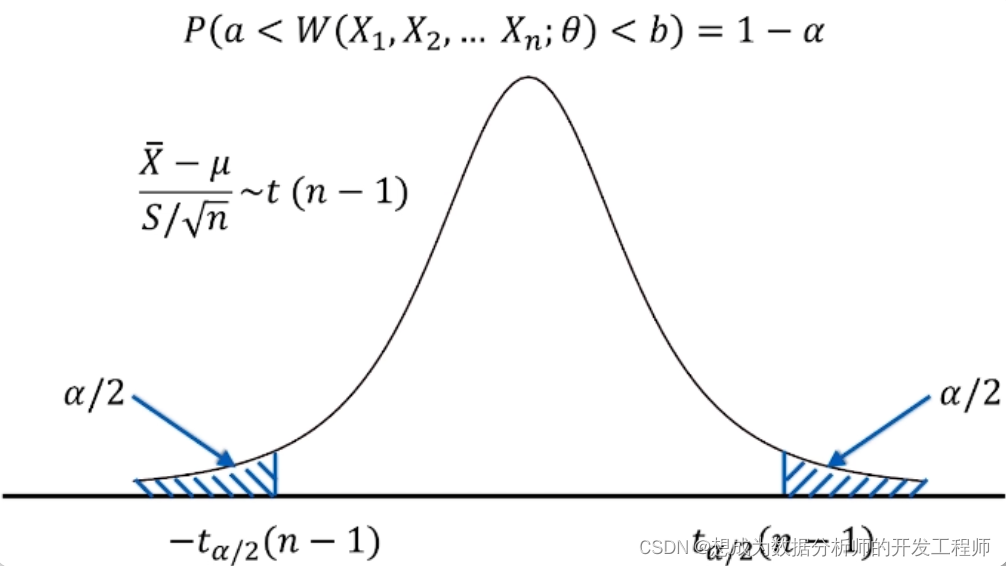
已知：总体X服从正态分布，且总体方差未知

求：均值的置信区间

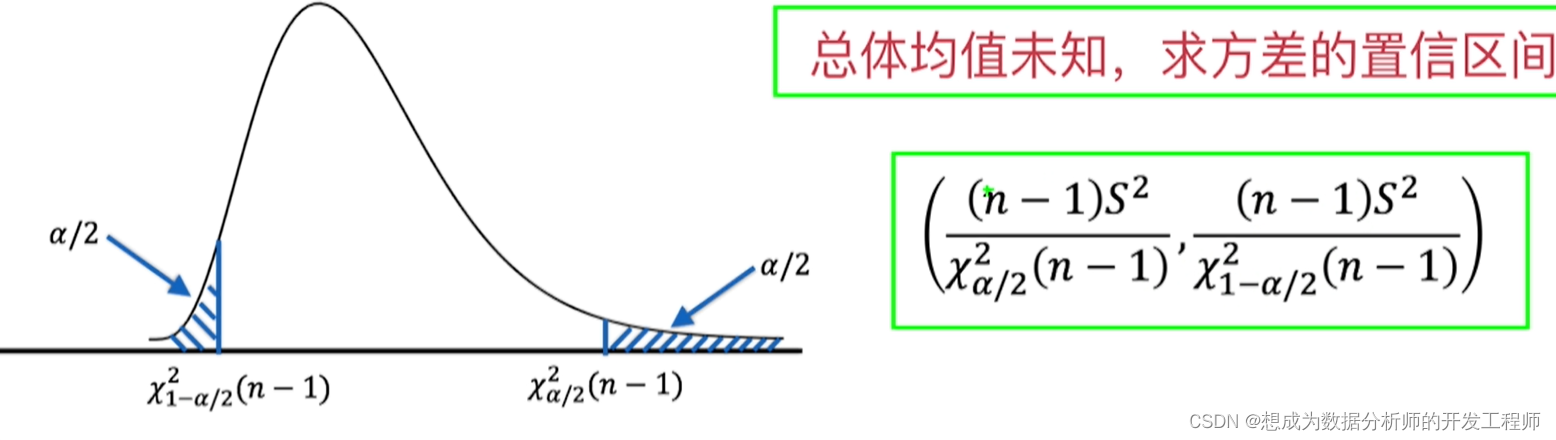
6.正态总体方差的置信区间(总体均值未知)

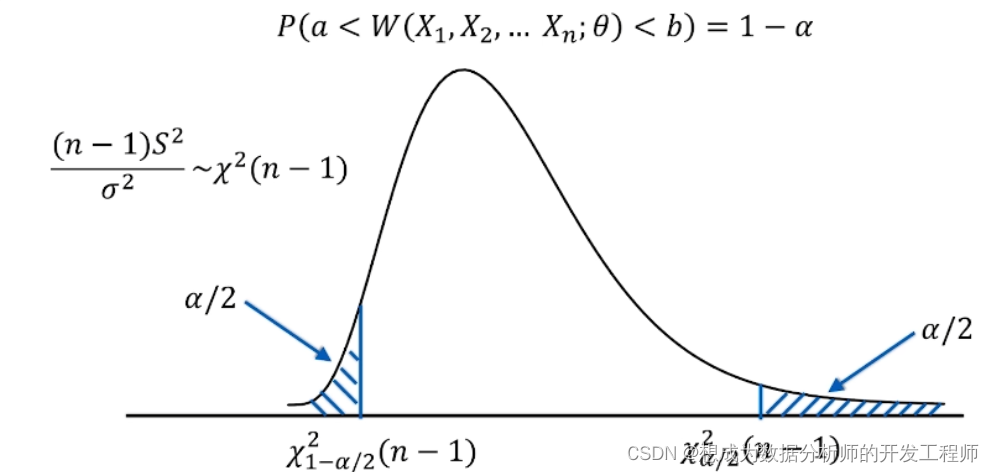
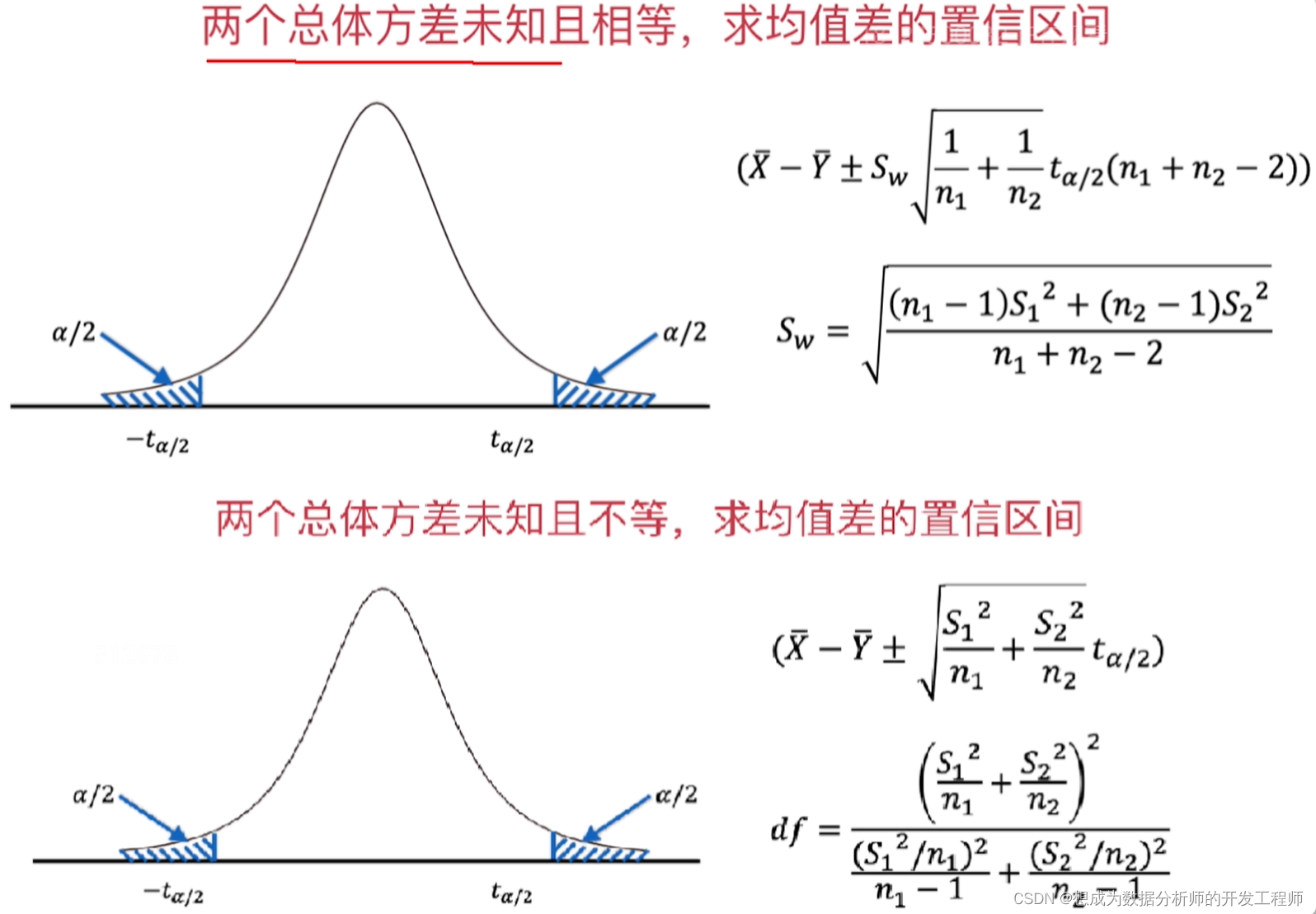
7.两正态总体均值差的置信区间(两个方差已知)

8.两正态总体均值差的置信区间(方差不等且未知)

9.Python实现均值估计（一个正态总体）

import numpy as np
from scipy.stats import norm, t, chi2 # 正态分布；t分布；卡方分布

# 计算一个正态总体均值的置信区间函数（分为是否已知方差两种情况）
def mean_ci_est(data, alpha, sigma=None): # data是原始数据，alpha是置信区间，sigma是方差
    n = len(data) # 样本容量
    sample_mean = np.mean(data) # 样本均值
    # 方差未知
    if sigma is None:
        s = np.std(data)
        se = s/np.sqrt(n)
        # t.ppf(alpha / 2, n-1) 返回左侧面积alpha/2对应的t值
        t_value = np.abs(t.ppf(alpha / 2, n-1)) 
        # 根据公式返回置信区间
        return sample_mean - se * t_value,sample_mean + se * t_value
    # 方差已知
    else:
        se = sigma / np.sqrt(n) # 标准差
        # norm.ppf(alpha/2)返回左侧面积为alpha/2对应的z值
        z_value = np.abs(norm.ppf(alpha/2))
        # 根据公式返回置信区间
        return sample_mean - se*z_value, sample_mean + se*z_value
salary_18 = [1484, 785, 1598, 1366, 1716, 1020, 1716, 785, 3113, 1601]
salary_35 = [902, 4508, 3809, 3923, 4276, 2065, 1601, 553, 3345, 2182]
# 样本均值是总体均值的无偏点估计，并调用函数计算均值的置信区间
print(np.mean(salary_18),mean_ci_est(salary_18,0.05))
print(np.mean(salary_35),mean_ci_est(salary_35,0.05))

10.Python实现方差估计(一个正态总体)

import numpy as np
from scipy.stats import norm, t, chi2 # 正态分布；t分布；卡方分布

# 定义计算方差的置信区间函数
def var_ci_est(data, alpha):
    n = len(data)# 样本容量
    s2 = np.var(data) # 样本方差
    # chi2.ppf(alpha/2,n-1) 返回左侧面积为alpha/2的卡方值
    chi2_low_value = chi2.ppf(alpha/2,n-1)
    # chi2.ppf(1-alpha/2,n-1) 返回左侧面积为1-alpha/2的卡方值
    chi2_upper_value = chi2.ppf(1-alpha/2,n-1)
    return (n-1) * s2 /chi2_upper_value, (n-1)*s2/chi2_low_value
salary_18 = [1484, 785, 1598, 1366, 1716, 1020, 1716, 785, 3113, 1601]
salary_35 = [902, 4508, 3809, 3923, 4276, 2065, 1601, 553, 3345, 2182]
# 样本方差是总体方差的无偏点估计
print(np.std(salary_18),np.var(salary_18),var_ci_est(salary_18,0.05))
print(np.std(salary_35),np.var(salary_35),var_ci_est(salary_35,0.05))

11.Python实现均值差的估计（两个正态总体）

import numpy as np
from scipy.stats import norm, t, chi2 # 正态分布；t分布；卡方分布

# 两个正态总体均值差的置信区间
def mean_diss_ci_t_est(data1, data2, alpha, equal=True):
    n1 = len(data1) # 样本1的容量
    n2 = len(data2) # 样本2的容量
    mean_diff = np.mean(data1)-np.mean(data2) # 两个样本的均值差（两个总体均值差的无偏估计）
    sample1_var = np.var(data1) # 样本1的方差
    sample2_var = np.var(data2) # 样本2的方差

    # 方差未知且相等
    if equal:
        sw = np.sqrt(((n1-1)*sample1_var + (n2-1)*sample2_var / (n1+n2-2)))
        t_value = np.abs(t.ppf(alpha/2, n1+n2-2))
        return mean_diff - sw*np.sqrt(1/n1+1/n2)*t_value, mean_diff + sw*np.sqrt(1/n1+1/n2)*t_value
    # 方差未知且不等
    else:
        df_numerator = (sample1_var/n1 + sample2_var/n2) **2 # 自由度分子
        df_denominator = (sample1_var/n1)**2/(n1-1) + (sample2_var/n2)**2 /(n2-1)# 自由度分母
        df = df_numerator / df_denominator # 自由度
        t_value = np.abs(t.ppf(alpha/2,df))
        return mean_diff - np.sqrt(sample1_var/n1 + sample2_var/n2) * t_value, mean_diff + np.sqrt(sample1_var/n1 + sample2_var/n2) * t_value

salary_18 = [1484, 785, 1598, 1366, 1716, 1020, 1716, 785, 3113, 1601]
salary_35 = [902, 4508, 3809, 3923, 4276, 2065, 1601, 553, 3345, 2182]

print(mean_diss_ci_t_est(salary_18, salary_35, 0.05, equal=True))
print(mean_diss_ci_t_est(salary_18, salary_35, 0.05, equal=False))

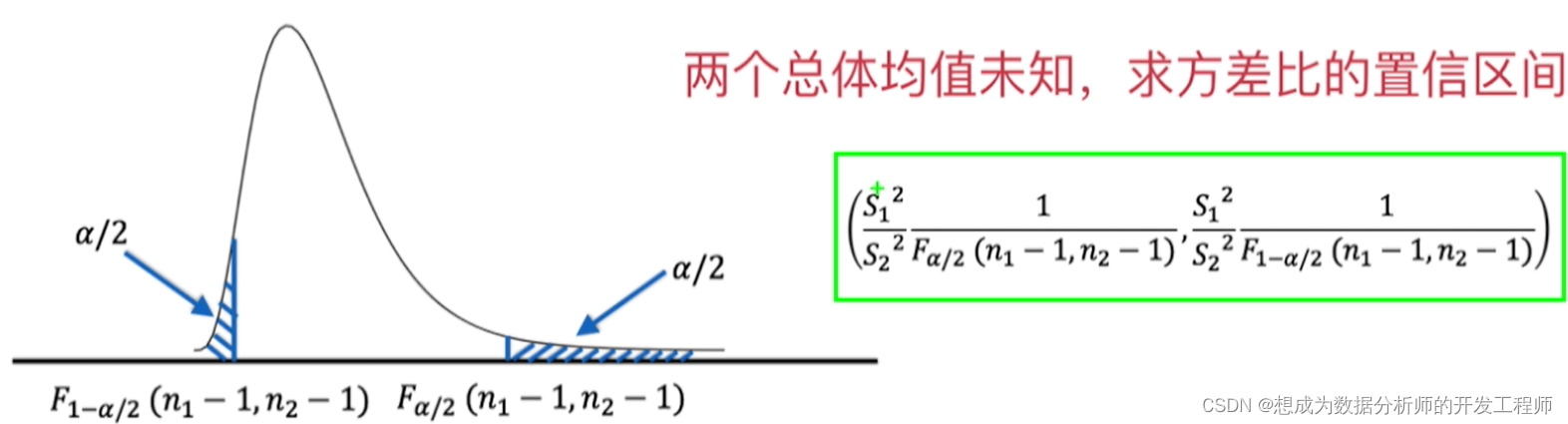
12.Python实现方差比的估计(两个正态总体)

import numpy as np
from scipy.stats import norm, t, chi2, f # 正态分布；t分布；卡方分布 f分布

# 定义一个实现方差比置信区间的函数
def var_ratio_ci_est(data1, data2, alpha):
    n1 = len(data1)
    n2 = len(data2)
    f_low_value = f.ppf(alpha/2, n1-1, n2-1) # 左侧临界值
    f_upper_value = f.ppf(1-alpha/2, n1-1, n2-1) # 右侧临界值
    var_ratio = np.var(data1) / np.var(data2)
    return var_ratio / f_upper_value, var_ratio/f_low_value
salary_18 = [1484, 785, 1598, 1366, 1716, 1020, 1716, 785, 3113, 1601]
salary_35 = [902, 4508, 3809, 3923, 4276, 2065, 1601, 553, 3345, 2182]


print(var_ratio_ci_est(salary_18, salary_35, 0.05))