问题 M: 喷水装置

目录

题目描述

样例输入

样例输出

代码

---

题目描述

长 L 米，宽 W 米的草坪里装有 n 个浇灌喷头。每个喷头都装在草坪中心线上（离两边各 W/2 米）。我们知道每个喷头的位置（离草坪中心线左端的距离），以及它能覆盖到的浇灌范围。

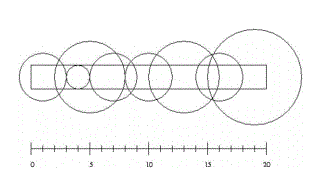
请问：如果要同时浇灌整块草坪，最少需要打开多少个喷头？

输入

输入包含若干组测试数据。

第一行一个整数 T 表示数据组数；

每组数据的第一行是整数 n、L 和 W；

接下来的 n行，每行包含两个整数，给出一个喷头的位置和浇灌半径（上面的示意图是样例输入第一组数据所描述的情况）。

输出

对每组测试数据输出一个数字，表示要浇灌整块草坪所需喷头数目的最小值。如果所有喷头都打开也不能浇灌整块草坪，则输出 −1 。

样例输入

3
8 20 2
5 3
4 1
1 2
7 2
10 2
13 3
16 2
19 4
3 10 1
3 5
9 3
6 1
3 10 1
5 3
1 1
9 1

样例输出

6
2
-1

提示

数据范围：

对于 100% 的数据，n≤15000。

代码

 

#include<bits/stdc++.h>
using namespace std;
int T;
int n, l, w, r, p, cnt;
struct app
{
    double s, e;
}a[20015];
 
bool cmp(app x, app y)
{
    return x.s < y.s;
}
void read()
{
    cnt = 0;
    scanf("%d%d%d", &n, &l, &w);
    for (int i = 1; i <= n; i++)
    {
        scanf("%d%d", &p, &r);
        if (r <= w / 2)  continue;  //直径无法完成w，没有用，直接不计入读入
        cnt++;
        a[cnt].s = p - sqrt((r * r) - (w * w / 4.0));
        a[cnt].e = p + sqrt((r * r) - (w * w / 4.0));
    }
}
void solve()
{
    int ans = 0;
    int i = 1;
    bool flag = 1;
    double t = 0;
    while (t < l)
    {
        ans++;
        double s = t;
        for (; a[i].s <= s && i <= cnt; i++)   //依次找能够覆盖L点的最大右端点
            if (t < a[i].e) t = a[i].e;
 
        if (t == s && s < l)    //中间有断层，且未到达终点，判断无解
        {
            flag = 0;
            printf("-1\n");
            break;
        }
    }
    if (flag) printf("%d\n", ans);
}
int main()
{
    scanf("%d", &T);
    while (T--)
    {
        read();
        sort(a + 1, a + cnt + 1, cmp);
        solve();
    }
    return 0;
}