算法设计与分析实验：分治算法

长安er

已于 2024-02-02 17:09:39 修改

阅读量984

点赞数 26

分类专栏：算法分析与设计文章标签：算法人工智能编程分治动态规划

于 2024-01-28 22:37:08 首次发布

本文链接：https://blog.csdn.net/m0_64198455/article/details/135901755

版权

算法分析与设计专栏收录该内容

12 篇文章 0 订阅

订阅专栏

一、旋转数组

力扣第189题

1.1 思路

思路I：分治

具体思路详细描述如下，突出了分治的思想：

首先判断特殊情况，如果k为0或者数组为空，则直接返回原数组。

计算实际需要向右轮转的步数new_k = k % len(nums)。这是因为当k大于数组长度时，轮转的效果与取模运算结果相同。

如果new_k等于0，则表示不需要进行任何操作，直接返回原数组。

分治的关键在于将数组分成两部分。将原数组划分为nums[:len(nums)-new_k]和nums[len(nums)-new_k:]两个子数组。

通过反转操作，将这两个子数组进行翻转。

最后将翻转后的两个子数组合并，得到最终结果。

通过以上思路，可以实现一个递归的分治算法来解决该问题。每次递归时，将问题规模缩小一半，直到达到基本情况（k=0或数组为空），然后开始回溯合并两个子问题的结果。

思路II：动态规划

使用动态规划的思想来实现数组元素向右轮转 k 个位置的解决步骤如下：

（1）对于一个长度为 n 的数组，向右轮转 k 个位置相当于将后 k 个元素移动到前面，同时将前 n-k 个元素移动到后面。因此，可以先将整个数组翻转，然后再将前 k 个元素和后 n-k 个元素分别翻转，最后得到结果。

（2）使用动态规划思想，定义状态和状态转移方程：

状态：dp[i] 表示数组中第 i 个元素在旋转后的位置。

状态转移方程：dp[(i+k) % n] = nums[i]，其中 n 是数组的长度，k 是旋转次数。

（3）初始化状态：

创建一个与原数组相同长度的新数组 dp，并将其所有元素初始化为 0。

动态规划转移：

（4）遍历原数组 nums，对于每个下标 i，将 nums[i] 赋值给 dp[(i+k) % n]。

返回结果：

返回新数组 dp。

1.2 代码

思路I：分治

def reverse(nums, start, end):
    while start < end:
        nums[start], nums[end] = nums[end], nums[start]
        start += 1
        end -= 1

def rotate(nums, k):
    if k == 0 or len(nums) == 0:
        return nums

    new_k = k % len(nums)
    if new_k == 0:
        return nums

    reverse(nums, 0, len(nums)-new_k-1)
    reverse(nums, len(nums)-new_k, len(nums)-1)
    reverse(nums, 0, len(nums)-1)

    return nums

# 示例 1
nums = [1,2,3,4,5,6,7]
k = 1
print(rotate(nums, k))

# 示例 2
nums = [1,2,3,4,5,6,7]
k = 4
print(rotate(nums, k))

# 示例 3
nums = [1,2,3,4,5,6,7]
k = 10
print(rotate(nums, k))

思路II：动态规划

def rotate(nums, k):
    n = len(nums)
    dp = [0] * n

    for i in range(n):
        dp[(i + k) % n] = nums[i]

    return dp

nums = [1, 2, 3, 4, 5, 6, 7]
k = 3
result = rotate(nums, k)
print(result)

1.3 时间/空间复杂度分析

在解决给定整数数组进行向右轮转 k 个位置的问题中，分治算法和动态规划算法的时间复杂度和空间复杂度如下：

（1）分治算法：

时间复杂度：分治算法的时间复杂度通常为 O(nlogn)。在这种情况下，分治算法可以通过三次翻转操作来实现数组的旋转，每次翻转操作的时间复杂度为 O(n/2)。因此，总的时间复杂度为 O(logn)，其中 n 是数组的长度。

空间复杂度：分治算法通常需要额外的空间来存储子问题的结果，因此它的空间复杂度较高。对于这个问题，需要创建一个长度与原数组相同的临时数组来存储中间结果，因此空间复杂度为 O(n)。

（2）动态规划算法：

时间复杂度：动态规划算法的时间复杂度通常为 O(n)。在这个问题中，动态规划步骤遍历了整个数组，对于每个元素都执行了一次赋值操作，因此总的时间复杂度为 O(n)，其中 n 是数组的长度。

空间复杂度：动态规划算法通常需要额外的空间来存储状态或中间结果。对于这个问题，需要创建一个与原数组相同长度的临时数组来存储旋转后的结果，因此空间复杂度为 O(n)。

综上所述，动态规划算法和分治算法在这个问题中具有相同的时间复杂度，都为 O(n)，但动态规划算法的空间复杂度更低，为 O(n)。因此，从时间复杂度和空间复杂度的角度来看，动态规划算法更优。

1.4 运行结果

以下分别是k=1，4，10的数组轮转结果

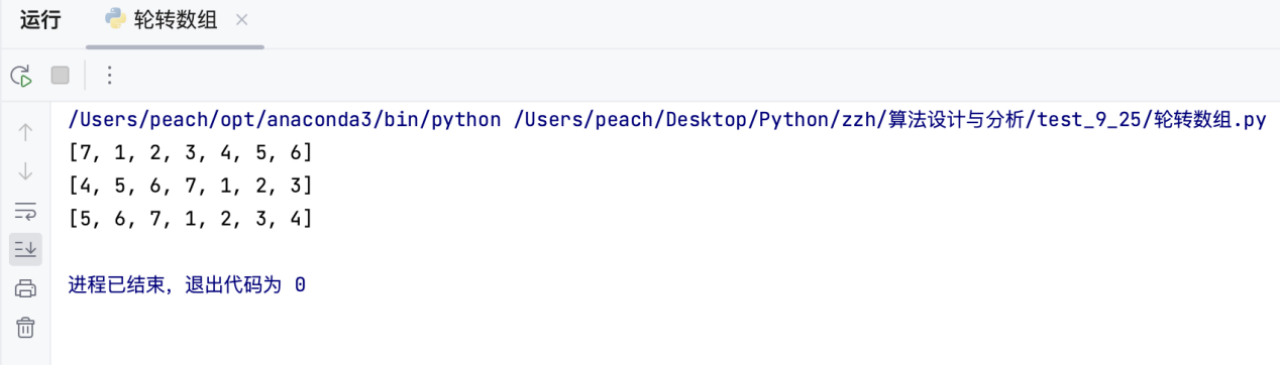
k=0时直接返回原数组

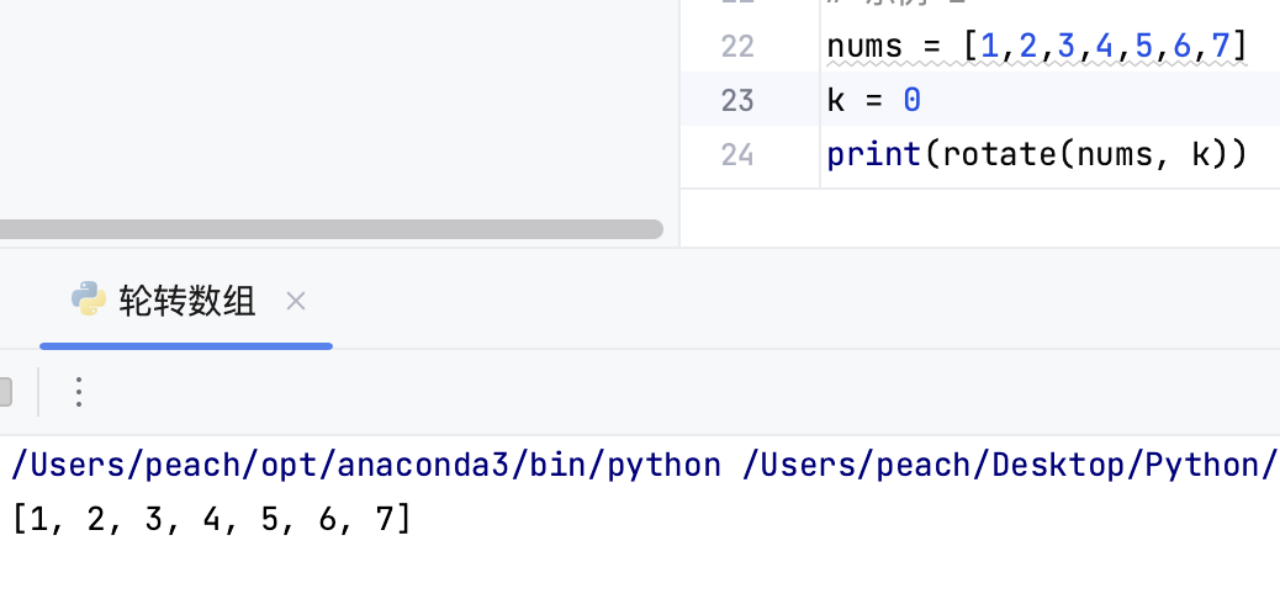
二、最大子序列和

力扣第53题

2.1 思路

思路I：分治
使用分治的思想解决最大子数组和问题，可以按照以下思路进行：

定义一个递归函数findMaxSubArray(nums, left, right)，用于在数组nums的left到right之间寻找最大子数组和。

判断递归的基本情况，即当left == right时，表示只有一个元素，直接返回该元素作为最大子数组和。

计算中间位置mid = (left + right) // 2，将数组划分为左右两个子数组。

递归调用findMaxSubArray分别在左右子数组中寻找最大子数组和，分别记为leftSum和rightSum。

分别从中间位置往左右两边遍历，计算包含中间元素的最大子数组和crossSum，分别记下左边界crossLeft和右边界crossRight。

比较三个和的大小，取最大值作为结果返回。

思路II：动态规划（DP）

使用动态规划的思想解决最大子数组和问题，可以按照以下步骤进行：

定义一个变量maxSum用于记录当前的最大和，初始化为第一个元素nums[0]。

定义一个变量curSum用于记录当前的连续子数组和，初始化为第一个元素nums[0]。

从数组的第二个元素开始遍历，对于每个元素num：

若curSum大于零，则将num加到curSum上；

若curSum小于或等于零，则将curSum更新为当前元素num。

在每次更新curSum时，比较curSum与maxSum的大小，将较大值赋给maxSum。

遍历结束后，maxSum即为最大子数组和。

2.2 代码

思路I：分治

def findMaxCrossingSubArray(nums, left, mid, right):
    crossLeftSum = float('-inf')
    crossSum = 0
    for i in range(mid, left-1, -1):
        crossSum += nums[i]
        if crossSum > crossLeftSum:
            crossLeftSum = crossSum

    crossRightSum = float('-inf')
    crossSum = 0
    for i in range(mid+1, right+1):
        crossSum += nums[i]
        if crossSum > crossRightSum:
            crossRightSum = crossSum

    return crossLeftSum + crossRightSum


def findMaxSubArray(nums, left, right):
    if left == right:
        return nums[left]

    mid = (left + right) // 2

    leftSum = findMaxSubArray(nums, left, mid)
    rightSum = findMaxSubArray(nums, mid+1, right)
    crossSum = findMaxCrossingSubArray(nums, left, mid, right)

    return max(leftSum, rightSum, crossSum)


nums = [-2, 1, -3, 4, -1, 2, 1, -5, 4]
result = findMaxSubArray(nums, 0, len(nums)-1)
print(result)

思路II：动态规划（DP）

def maxSubArray(nums):
    maxSum = nums[0]
    curSum = nums[0]

    for i in range(1, len(nums)):
        if curSum > 0:
            curSum += nums[i]
        else:
            curSum = nums[i]

        maxSum = max(maxSum, curSum)

    return maxSum


nums = [-2, 1, -3, 4, -1, 2, 1, -5, 4]
result = maxSubArray(nums)
print(result)

观察两种思路的代码量，可知使用动态规划思想较为简洁

2.3 复杂度分析

在解决最大子数组和问题上，动态规划算法的时间复杂度和空间复杂度较低，而分治算法的时间复杂度和空间复杂度较高。

动态规划算法的时间复杂度为 O(n)，其中 n 是数组的长度。动态规划算法通过自底向上的方式逐步求解子问题，并利用子问题的解来构建更大规模问题的解。在最大子数组和问题中，动态规划算法通过维护一个全局的最优解和一个局部的当前子数组和来进行计算。通过遍历一次数组，可以在线性时间内找到最大子数组和。

另一方面，分治算法的时间复杂度为 O(nlogn)。分治算法将原问题划分成规模较小的子问题，并通过递归的方式求解子问题，然后将子问题的解合并起来得到原问题的解。在最大子数组和问题中，分治算法将数组划分成两个子数组，在子数组内递归地求解最大子数组和，然后通过合并子数组的解来计算跨越两个子数组的最大子数组和。这个过程需要消耗较多的时间来合并子问题的解。

在空间复杂度方面，动态规划算法只需要常数级别的额外空间来保存一些状态变量和临时结果，因此空间复杂度为 O(1)。而分治算法需要额外的空间来保存递归调用的栈帧和临时数组，空间复杂度为 O(logn)。

综上所述，动态规划算法在时间复杂度和空间复杂度上都比分治算法更优。因此，在解决最大子数组和问题上，动态规划算法是更为高效的选择。

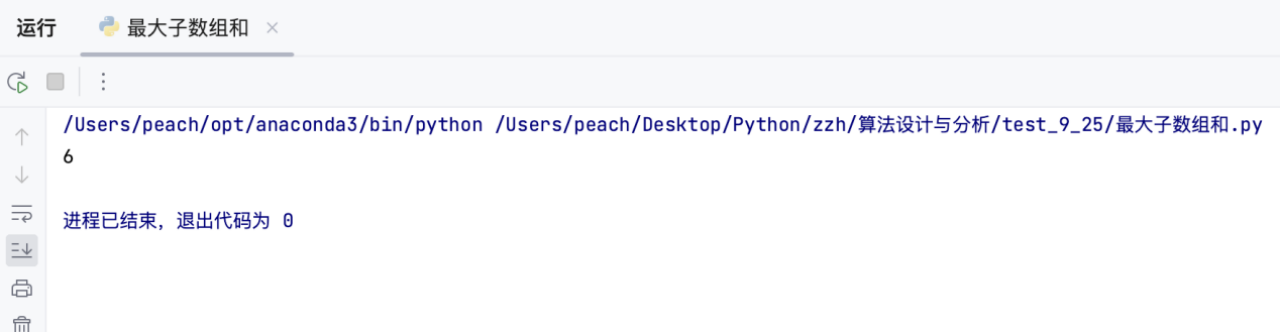
2.4 运行结果

最大子数组为[4, -1, 2, 1]

三、斐波那契数列

力扣第509题

3.1 思路

思路I：动态规划

使用动态规划的思路解决斐波那契数列问题的详细思路如下：

定义一个列表 fib 用于存储斐波那契数列的结果，初始化为 [0, 1]。列表 fib 的下标表示斐波那契数列的索引，对应的值为该索引对应的斐波那契数。

若输入的 n 小于等于 1，则直接返回 fib[n]，因为在这种情况下斐波那契数列的值即为 n。

从索引 2 开始遍历到 n，对于每个索引 i：

计算 fib[i] 的值，为 fib[i-1] + fib[i-2]，即前两个数的和。

将计算得到的值添加到 fib 列表中。

遍历结束后，fib[n] 即为所求的斐波那契数。

思路II：递归算法

递归解法可以将问题分解为更小规模的子问题，并利用已知结果来求解。

对于斐波那契数列，可以按照以下步骤进行递归计算：

定义基准情况：当 n 等于 0 或 1 时，直接返回 n（即 F(0) = 0，F(1) = 1），这是递归的终止条件。

定义递推关系：当 n 大于 1 时，斐波那契数列的第 n 项可以通过计算前面两项的和来获得，即 F(n) = F(n-1) + F(n-2)。

递归调用：在计算 F(n) 时，可以通过递归调用来分别计算 F(n-1) 和 F(n-2) 的值。

3.2 代码

思路I：动态规划

def fib(n):
    if n <= 1:
        return n

    fib = [0, 1]
    for i in range(2, n + 1):
        fib.append(fib[i - 1] + fib[i - 2])

    return fib[n]

n = 2
result = fib(n)
print(result)

思路II：递归算法

def fibonacci(n):
    if n == 0:
        return 0
    elif n == 1:
        return 1
    else:
        return fibonacci(n-1) + fibonacci(n-2)

n = 2
result = fibonacci(n)
print(result)

3.3 时间/空间复杂度分析

在斐波那契数列问题上，递归算法和动态规划算法的时间复杂度和空间复杂度是不同的。

（1）递归算法的时间复杂度和空间复杂度：

时间复杂度：递归算法的时间复杂度往往较高。在递归求解斐波那契数列时，每个项的计算需要依赖前两项的计算结果，因此需要逐层递归，导致时间复杂度为指数级别。具体而言，递归算法的时间复杂度为 O(2^n)。

空间复杂度：递归算法的空间复杂度也较高。每次进行递归调用时，需要在内存中维护一个递归栈，用于保存递归函数的局部变量、返回地址等信息，直到递归结束才释放。在递归求解斐波那契数列时，递归栈的深度与n 相关，所以空间复杂度为 O(n)。

（2）动态规划算法的时间复杂度和空间复杂度：

时间复杂度：动态规划算法通常能够将指数级别的时间复杂度降低到多项式级别。在斐波那契数列的动态规划算法中，将问题拆解为计算前面两项的和，并利用迭代的方式逐步求解，时间复杂度为 O(n)。

空间复杂度：动态规划算法的空间复杂度主要取决于存储计算结果的数组或表格。在斐波那契数列的动态规划算法中，只需使用一个长度为 n+1 的数组来保存每个位置的斐波那契数值，因此空间复杂度为 O(n)。

综上所述，动态规划算法相对于递归算法在时间复杂度和空间复杂度上都具有优势。递归算法由于重复计算和递归栈的开销，时间复杂度较高；而动态规划算法通过以空间换时间的思想，将指数级别的时间复杂度降低到多项式级别，并且空间复杂度也较低。因此，对于斐波那契数列问题，推荐使用动态规划算法来获得更高的效率。

四、逆序对

力扣第51题

4.1 思路

使用分治的思想解决股票交易中的「交易逆序对」问题的详细思路如下：

定义函数 merge_sort(nums, l, r)，该函数用于对 nums 数组中从索引 l 到 r 的元素进行归并排序，并返回该区间内「交易逆序对」的个数。当 l == r 时，无法形成逆序对，直接返回 0。

在 merge_sort 函数中，将区间 [l, mid] 和区间 [mid+1, r] 分别进行递归，得到它们各自的逆序对数量 left 和 right。

对区间 [l, mid] 和区间 [mid+1, r] 进行归并，在归并的过程中计算跨越两个区间的逆序对数量 cross。

设置两个指针 i 和 j 分别指向区间 [l, mid] 和区间 [mid+1, r] 的起始位置。

每次比较 nums[i] 和 nums[j] 的大小，若 nums[i] > nums[j] 则说明存在一个逆序对，逆序对数量为 mid-i+1，因为左半部分区间 [l, mid] 中剩余的所有元素都大于 nums[j]。

将较小的元素添加到临时数组 tmp 中，并将对应指针 i 或 j 向后移动一位。

将归并得到的排序后的区间 [l, r] 赋值回原数组 nums 中，然后返回 left + right + cross。

4.2 代码

def merge_sort(nums, l, r):
    if l == r:
        return 0

    mid = (l + r) // 2
    left = merge_sort(nums, l, mid)
    right = merge_sort(nums, mid+1, r)

    tmp = []
    i, j, cross = l, mid+1, 0
    while i <= mid and j <= r:
        if nums[i] > nums[j]:
            cross += (mid - i + 1)
            tmp.append(nums[j])
            j += 1
        else:
            tmp.append(nums[i])
            i += 1

    while i <= mid:
        tmp.append(nums[i])
        i += 1
    while j <= r:
        tmp.append(nums[j])
        j += 1

    nums[l:r+1] = tmp
    return left + right + cross

#示例一
record_1= [9, 7, 5, 4, 6]
result_1 = merge_sort(record_1, 0, len(record_1)-1)
print(result_1)


#示例二
record_2= [8, 7, 0, 4, 5]
result_2 = merge_sort(record_2, 0, len(record_2)-1)
print(result_2)

4.3 运行结果

第一个数组 [9, 7, 5, 4, 6]逆序对如下所示有8个，分别是(9, 7), (9, 5), (9, 4), (9, 6), (7, 5), (7, 4), (7, 6), (5, 4)。

第二个数组 [8, 7, 0, 4, 5]逆序对如下所示有7个，分别是(8, 7), (8, 0), (8, 4), (8, 5), (7, 0), (7, 4), (7, 5)。

长安er

关注

26
点赞
踩
22

收藏

觉得还不错? 一键收藏
打赏
0
评论
算法设计与分析实验：分治算法

分治算法将原问题划分成规模较小的子问题，并通过递归的方式求解子问题，然后将子问题的解合并起来得到原问题的解。综上所述，动态规划算法和分治算法在这个问题中具有相同的时间复杂度，都为 O(n)，但动态规划算法的空间复杂度更低，为 O(n)。在斐波那契数列的动态规划算法中，将问题拆解为计算前面两项的和，并利用迭代的方式逐步求解，时间复杂度为 O(n)。逆序对如下所示有8个，分别是(9, 7), (9, 5), (9, 4), (9, 6), (7, 5), (7, 4), (7, 6), (5, 4)。
复制链接

扫一扫