自控第三章线性系统的时域分析法（超详细适合复习看，考点全覆盖）

ZnDream66

于 2021-11-17 01:53:21 发布

阅读量5.1k

点赞数 11

分类专栏：自动控制原理笔记文章标签：经验分享

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/m0_64229842/article/details/121345247

版权

目录

1.线性系统的时域性能指标

1.1延迟时间

1.2上升时间

1.3峰值时间

1.4调节时间

1.6稳态误差

2.一阶系统的时域分析

2.1一阶系统的单位阶跃响应

3.二阶系统的时域分析

3.1二阶系统的单位阶跃响应

3.1.1过阻尼()

3.1.2临界阻尼()

3.1.3零阻尼()

3.1.4欠阻尼()

3.2欠阻尼二阶系统的瞬态响应指标分析

3.2.1上升时间

3.2.2峰值时间

3.2.3t调节时间

4.二阶系统的改善

4.1 误差的PD(比例—微分)控制

4.3 PD控制与测速反馈控制的比较

5.线性系统的稳定性分析

5.1线性系统稳定的充分必要条件

5.2劳斯稳定判据

5.2.1 劳斯表

5.2.2劳斯判据的判定规则

5.2.3劳斯稳定判据的特殊情况

6.控制系统的稳态误差

6.1 给定输入信号下的稳态误差

6.2系统的类型

6.3不同输入信号下的稳态误差

6.3.1阶跃输入信号下稳态误差

6.3.2 斜坡输入信号下稳态误差

6.3.3 抛物线输入信号下稳态误差

6.4扰动信号下的稳态误差

1.线性系统的时域性能指标

线性系统的时域性能指标是在单位阶跃函数作用下的响应指标

1.1延迟时间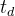 $t_{d}$

响应曲线第一次到达最大值一半的时间

1.2上升时间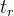 $t_{r}$

响应曲线第一次到达稳态值的时间

1.3峰值时间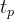 $t_{p}$

响应曲线第一次到达峰值的时间

1.4调节时间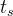 $t_{s}$

响应曲线第一次到达区间[0.95 $c(\infty )$ ,1.05 $c(\infty )$ ]内的时间（或者2%）

1.5超调量 $\sigma %$

$\sigma %=\frac{c(t)_{max}-c(\infty )}{c(\infty )}$

1.6稳态误差 $e_{ss}$

$e_{ss}=\lim_{t\rightarrow \infty }e(t)=\lim_{t\rightarrow \infty }(r(t)-b(t))$

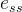
2.一阶系统的时域分析

2.1一阶系统的单位阶跃响应

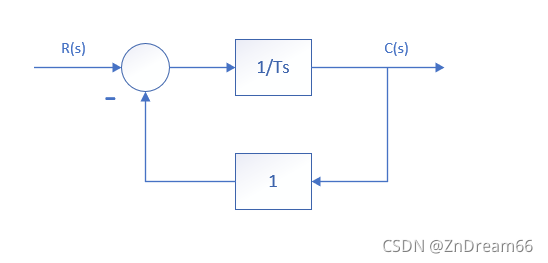
可以看到一阶系统的单位阶跃响应随着指数函数单调上升，稳态值为1。

3.二阶系统的时域分析

3.1二阶系统的单位阶跃响应

特征根为 $s_{1,2}=-\zeta \omega _{n}\pm \omega _{n}\sqrt{\zeta ^{2}-1}$

3.1.1过阻尼( $\zeta >1$ )

在这情况下闭环传递函数的两个极点都是实数，则响应曲线为单调函数，利用终值定理和初值定理可以得到响应曲线初始为0，终值为1，所有函数曲线单调递增，当 $\zeta$ 增大时一个极点逐渐远离原点，一个极点逐渐靠近原点，远离原点的极点的影响可以忽略不计，可以把这时候的二阶系统简化为一阶系统分析，工程上当 $\zeta >1.25$ 便可近似为一阶分析。如果s2到原点的距离超过了s1到原点距离的四倍，则调节时间 $t_{s}\approx 3T_{1}=3\frac{-1}{s_{1}}$ .

3.1.2临界阻尼( $\zeta =1$ )

此情况下两个闭环极点重合

该响应曲线也是单调递增的，初值为0终值为1，而且快速性比较好。

3.1.3零阻尼( $\zeta =0$ )

响应曲线是振幅为一，角频率为 $\omega _{n}$ 的等幅振荡。

3.1.4欠阻尼( $0<\zeta <1$ )

当 $0<\zeta <1$ 时，闭环函数的两个极点是共轭复数，

$s_{1,2}=-\zeta \omega _{n}\pm \omega _{n}\sqrt{\zeta ^{2}-1}$ ，响应曲线是振荡曲线，欠阻尼二阶系统的单位阶跃响应为：

其中 $\omega _{d}=\omega _{n}\sqrt{1-\zeta ^{2}}$ ，极点的实部 $\zeta \omega _{n}$ 为衰减系数决定了衰减的快慢，极点的虚部为振荡频率，其中 $\beta =acrcos\zeta$ ,称为阻尼角。可以知道阻尼系数对二阶系统单位阶跃响应有很大影响，当 $\zeta$ 越小时，系统的上升时间越短但平稳性差， $\zeta$ 增大时，超调量减小，衰减加快，振荡性降低，平稳性好， $\zeta$ 增大到1及大于1以后，响应变为非周期无振荡的，但响应速度明显变慢，通常取 $\zeta$ =0.4~0.8，此时系统的超调量适度，调节时间较短，工程上将 $\zeta$ =0.707附近的系统称为二阶最优系统，0.707为最佳阻尼系数。

3.2欠阻尼二阶系统的瞬态响应指标分析

3.2.1上升时间

最低0.47元/天解锁文章

评论 24

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

打赏作者

ZnDream66 你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20

扫码支付：¥1

获取中

扫码支付

您的余额不足，请更换扫码支付或充值

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。