网络系统建模与仿真复习

#包括MATLAB基础，图论，二叉树#

MATLAB基础

    
str1 = 'blink'
str2 = 'bliss'
str3 = 'god will blink you'
result = strcmp(str1,str2) %比较长度，字母
result1 = strcmpi(str1,str2) %忽略大小写
result2 = strncmp(str1,str2,3) %比较前面n个字母是否一致

strrep(str3,str1,str2) %把str3中的str1用str2代替
strfind(str3,'wi') %查找出现的位置

x = 2;
x = int2str(x)%整数转字符串
y = '102';
y = num2str(y)%字符串转整数
z = '11011001';
z = bin2dec(z)%二进制转十进制

%程序设计 3*x-6
% x = input('a=');
% b = input('b=');
% c = input('c=');
% d = sqrt(b*b-4*a*c);
% result = [(-b+d)/(2*a),(-b-d)/(2*a)];
% disp(['x1=',num2str(result(1)),'x2=',num2str(result(2))])
choice = 1
if choice == 1
    disp('我是1')
else
    disp('我不是1')
end
%switch-case结果组不能添加条件吗，只能是具体的值
price = input('price = ?');
switch fix(price/100)
    case {0,1}
        disp('没有折扣')
    case {2,3,4}
        disp('有折扣')
    otherwise
        disp('i dont konw')
end
%try-catch先执行try的内容，发生了错误把错误的内容赋给lasterr，再执行catch的内容
A=[1,2,3;4,5,6]; 
B=[7,8,9;10,11,12];
try
    A*B
catch
    A.*B
end
%把每一列的值赋给循环变量
a=[12,13,14;15,16,17;18,19,20;21,22,23];
s = 0;
for k = a
    s = s+k;
end
%寻找第一个整除63的数-
for m =1:1000
    if rem(m,63)==0
        continue
    end
    break
end
%列出1000以内除13余2的所有整数
num = [];
for i = 1:1000
    if rem(i,13)==2
        num= [num,i];
    end
end
num;

%%符号替换
% syms x;
% f = sin(x);
% subs(f,x,y)%表示将函数表达式f(x)中x用y替换

%max返回的是一个[行向量，位序]，行向量的值对应每个矩阵中的每一列的最大值。位序是指每个最大值对应的行号
x = [3 5 7;2 6 5;1 9 3];
[m,n] = max(x)
max(x,[],1)%返回的是一个行向量，对应每一列的最大值，等同于上面一个
max(x,[],2)%返回的是一个列向量，对应每一行的最大值
maxmuim  = max(max(m))%寻找最大值
clear sum;sum(x)%返回一个行向量，作为每一列的和
clear sum;sum(x,2)%返回一个列向量，是各行之和
clear prod;prod = prod(x)%返回一个行向量，是各列之积
clear prod;prod = prod(x,2)%返回一个列向量，是各行之积

clear mean;mean(x)%返回一个行向量，是每一列的均值 === mean(x,1)
clear mean;median(x)%返回一个行向量，是每一列的中值 === median(x,1)
clear mean;mean(x,2)%返回一个列向量，是每一行的平均值
clear mean;median(x,2)%返回一个列向量，是每一行的中值

length(x)%返回矩阵的最大维数
size(x)%返回矩阵的行数和列数

index = input('');
fibal = [1,1];
for i=3:index
    fibal(i) = fibal(i-1)+fibal(i-2);
end
fibal(1:i)

图论基础

邻接表

缺点：无法看出一个完整的网络类型是怎样的

邻接矩阵

描述节点与节点之间的联通关系

 特点：对称轴上的元素全为0，矩阵关于斜对角线对称

关联矩阵

描述节点和边的联通关系

转换

邻接矩阵和邻接表、关联矩阵的转换

邻接表——>邻接矩阵：邻接表中每取出一行，前一个数定位第几行，后一个数定位第几列。

邻接矩阵——>邻接表：取出每一个为1的元素的行值和列值，对应存入邻接表。

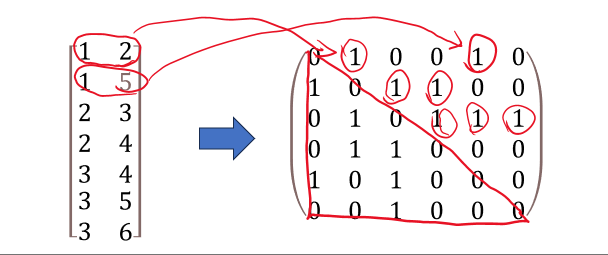
代码实现：邻接表——邻接矩阵

邻接表转邻接矩阵
function adj = edges2adj(edge,n)
    %ÁÚ½Ó±íתÁÚ½Ó¾ØÕó
    adj = zeros(n,n);
    for i = 1:size(edge,1)
        adj(edge(i,1),edge(i,2)) = 1;
    end
end

               邻接矩阵——邻接表

邻接矩阵转邻接表
function edge = edge2adj(G)
    n = size(G,1);
    edge = [];
    [x,y] = find(G);
    edge = [edge;x,y];
end

                邻接矩阵——关联矩阵（无向图）

邻接矩阵转关联矩阵（无向图）
function inc = adj2inc(G)
    G = triu(G);
    n = size(G,1);%½ÚµãÊý
    v = sum(sum(G));%±ßÊý
    inc = zeros(n,v);%³õʼ»¯¹ØÁª¾ØÕó
    k = 1;
    for i = 1:n
        for j=1:n
            if G(i,j)~=0
                inc(i,k) = 1;
                inc(j,k) = 1;
                k = k+1;
            end
        end
    end
end

                关联矩阵——邻接矩阵（无向图）

关联矩阵转邻接矩阵（无向图）
function G = inc2adj(inc)
    n = size(inc,1);
    G = zeros(n,n);
    for i = 1:n
        [x,y] = find(inc(:,i));
        G(x(1),x(2)) = 1;
        G(x(2),x(1)) = 1;
    end
end

                邻接矩阵——关联矩阵（有向图）

                与无向图一样，但是终点到边需要记为-1，以示区别

                关联矩阵——邻接矩阵（有向图）

                与无向图一样，在遍历边的时候结果为1，置邻接矩阵对应位置为1；相反置-1

        

function G = inc2adj_directed(inc)
    m = size(inc,2);%»ñÈ¡±ßÊý
    n = size(inc,1);%»ñÈ¡½ÚµãÊý
    G = zeros(n,n);
    for i=1:m
        index = find(inc(:,i)~=0);
        if inc(index(1),i)==1
            G(index(1),index(2)) = 1;%Æðµã
        else
            G(index(2),index(1)) = 1;%ÖÕµã
        end
    end
end

                可视化

info = graph(G);
plot(G);
plot(G,'upper');%只绘制上三角
plot(G,'lowwer');%绘制下三角

info = digraph(G)%有向图
plot(info);

网络路径与连通性

概念

在无向图中每条边都有两端，边数*2 = 图中所有结点的度数

自回避路径

与自身没有交叉的路径成为自回避路径，典型代表：测地路径（最短路径）、哈密顿路径

计算长度为2的路径

最短路径

测地路径必然是自回避的，自相交路径不是测地路径

测地路径并非一定或唯一的，两个顶点之间很可能有两条或更多条具有相同长度的测地路径

图的直径：图中任意一对相互连接的顶点之间的最长测地路径长度。两个互不联通的节点之间有无穷大的测地距离是无穷大

加权网络的最短路径：节点(u,v)之间的边权之和达到最小的路

Dijkstra算法

只能适用于权值为正的网络。节点a到图中任意一个节点的最短路径，掌握寻找的过程

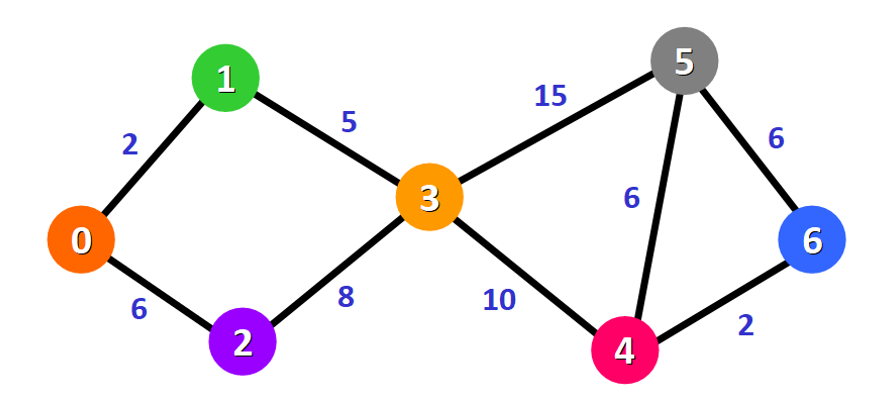
Floyd算法

解决任意两点之间的最短路径算法，可以解决有向图或负权的最短路径，同时可以用于计算有向图的传递闭包。时间复杂度ON3,空间复杂度ON2

掌握点到任意点的最短距离寻找过程，以及矩阵的更新过程

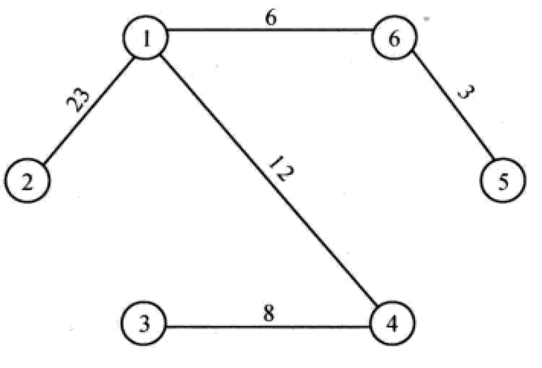
 寻找任意两点之间的最短路径过程

需要增加一个额外的矩阵来记录从节点i到节点j时经过的中间节点，比如在以A作为中转站的时候，更新距离矩阵（C->B、B->C）时，也需要在标记矩阵的对应位置写上节点A（B行C列，C行B列）

网络连通性

连通网络：存在两个顶点之间不存在路径的网络称为非连通网络

联通网络：网络中任何两个顶点之间都能找到一条路径就是连通网络

可达矩阵：节点i和节点j之间可达，以1表示；不可达以0表示

网络节点度数计算

    degrees = [];
    n = size(G,1);
    edges = [];
    G = triu(G);%转换成上三角矩阵
    [x,y] = find(G);
    edges = [x,y];
    for i = 1:size(G,1)
        counts = find(edges == i);
        degrees = [degrees,length(counts)];
    end

或者

degrees = [];
degrees = sum(G);

可达矩阵的意义：描述线图中，从任一节点到另一节点之间是否存在路。如果在图中两个节点之间有路，则【必然存在长度小于等于n-1的通路】

可达矩阵的计算

邻接矩阵转可达矩阵

邻接矩阵转可达矩阵
W = zeros(n,n);
for i = 1:size(G,1)
        W = G+G^i;
end
W(W~=0) = 1;
[m,l] = find(W~=1);
if l>0
disp('disconnected');
else
disp('connected');
end

可达矩阵判断网络是否全联通

function judgeliantong(W)
[a,b] = find(W==0);
l = length(b);
if l>0
    disp('非全联通');
else
    disp('全联通');
end
end

分支

        分支或连通块：同一个网络中，所有存在相互路径的节点和边组成的子图称为分支或连通块

        分支：网络中顶点和边的子集，子集中任何两个顶点之间至少存在一条路径

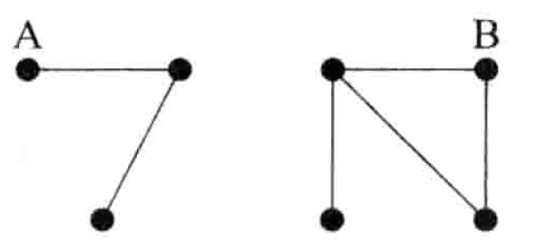
        连通网络必然只有一个分支，与其他顶点没有连接的孤立节点被当成规模为1的分支，任何一个顶点属于且只属于一个分支

        最大子集：网络中其他顶点都不能被添加到这个子集中

        网络中存在分支，那么对应的邻接矩阵可以写成分块对角形式，意味着矩阵的非零元素都被限制在沿对角线的正方形块中

       

        求矩阵的秩：rref(G) 或 rank(G)

        图的连通分支数 = n-rank(可达矩阵)

        求连通分支片的大小（尺寸)、节点属于哪个分支

网络节点的度

       邻接矩阵转换成邻接链表，然后计算对应节点在所有结点对中出现的次数

%使用之前的邻接矩阵G转邻接表W
W = adj2edge(G);
value = tabulate(W(:));统计邻接表中各个元素出现的次数,value返回[元素-出现次数-出现频率]的矩阵
value(:,2);

%如果不允许使用tablulate
degree = [];
for i=1:size(G,1)
    index = find(W==i);
    degree(i) = length(index);
end
disp(degree);

      

节点收缩算法

将拥有最大度的节点及其直接相连的邻居节点收缩至一个新的节点中，该节点负责存储收缩的所有节点信息及其相互之间的连边信息

function [S,Q] = count(G)
%S连通分支数
%Q每个节点属于的连通分支
    S = 0;
    n = size(G,1);
    Q = zeros(n,1);
    C = 1;
    for i =1:n
        for j =(i+1):n
            if G(i,j) == 1
                if Q(i)==Q(j)
                    if Q(i)==0
                        Q(i) = C;
                        Q(j) = C;
                        C = C+1;
                        S = S+1;
                    end
                else
                    if Q(i)==0
                        Q(i) = Q(j);
                    elseif Q(j)==0
                        Q(j) = Q(i)
                    else
                        for k = 1:n
                            if Q(k) == Q(i)
                                Q(k) = Q(j);
                            end
                            S = S-1;%ºÏ²¢·ÖÖ§
                        end
                    end
                end
            end
        end
    end
end

树

概念

不包含圈的连通图称为树，树中度为1的顶点称为叶，亦称为悬挂点，树的边称为树枝

树的判定方法

图G是连通的，且只有N-1条边

图G是连通的，并且不包含边

图G不包含圈，且有N-1条边

图G中任意两个顶点之间有且仅有一条路径

图G中任意一条边都是桥。即去除图G中任意一条边都会使图变得不连通

自由树：连通无环图可以称为一棵树，在没有特定指定其节点特性时，这棵树称为自由树

如何判断图联通，且边数为N-1?

• 去除自边（对角线上的非零元素）
• 计算边数（判断是否为N-1）
• 计算连通性（邻接矩阵转可达矩阵）
• 判断环（方法一）
  • 判环的思路
  • 
  • ①判断节点的直连边数，使用sum函数求出每个节点的直连边数，使用find函数找出其中边数为1的节点。

    edgecounts = sum(G);
    One_edge_list = find(edgecounts == 1);

• ②删除边数为1的节点在邻接矩阵中的行和边

• ③反复迭代，直到找不到边数为1的节点；如果最后还剩节点，但是找不到边为1的节点了，说明有环；如果已经没有节点了，说明没环

另一种简化判断逻辑，只要当图中的边数比（N-1）更大的时候就一定有环（方法二）

function loop = is_loop(G)
    loop = false;
    N = sum(G,1);%节点个数
    G = triu(G);
    V = sum(sum(G));%边数
    if V>N-1
        loop = true;
    end


end

广度优先搜索BFS

        判断图的连通性，并找出图的一颗生成树

        适用于解决最短、最小路径等问题

        

function traverse_route = bfs(G,start_node)
    n = size(G,1);%»ñÈ¡½Úµã¸öÊý
    visited = false(1,n);
    visited(start_node) = true;%´ÓÆðʼ½Úµã¿ªÊ¼
    Queue = start_node;
    traverse_route = [];%±éÀú·¾¶
    while ~isempty(Queue)
        head = Queue(1);
        Queue = Queue(2:end);
        traverse_route =[traverse_route,head];
        %Ñ°ÕÒ³ö¶Ó½ÚµãµÄÁÚ¾Ó½Úµã
        neighbors = find(G(head,:)==1);
        for neighbor = neighbors
            if ~visited(neighbor)
                Queue = [Queue,neighbor];
                visited(neighbor) = true;
            end
        end
    end
end

深度优先搜索DFS

        求生成树，割点，块和平面图嵌入算法

function traverse_route = dfs(G,start_node)
    n = size(G,1); %½Úµã¸öÊý
    visited = false(1,n);
    stack = start_node;
    traverse_route = [];
    if start_node<1 | start_node >n
        error('½Úµã±àºÅ³¬³ö·¶Î§');
    end
    while ~isempty(stack)
       head = stack(1);%µ¯³öÕ»¶¥
       stack = stack(2:end);
       if visited(head) == false
           visited(head) = true;%Ö÷ÃÎÊ
           traverse_route = [traverse_route,head];%¼ÓÈë·ÃÎÊ·¾¶
            fprintf('Visited node: %d\n', head);  
           neighbors = find(G(head,:)~=0);%Ñ°ÕÒµ¯³öµÄÔªËصÄ
           for neighbor = neighbors
               if visited(neighbor) == false
                   stack = [neighbor,stack]
               end
           end
       end
    end
end

 DFS VS BFS

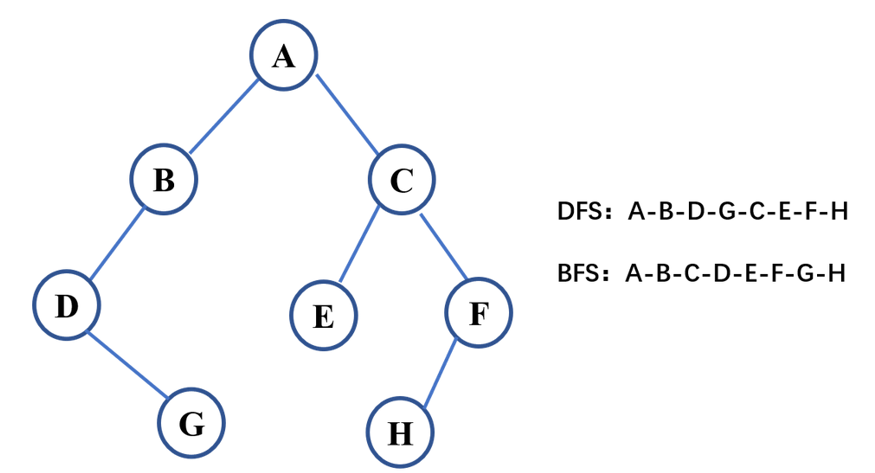
生成树

一个连通图的生成树是指包含全部的N个顶点，但只构成一棵树的N-1条边

生成树并不唯一，包含n个顶点的无向完全图最多包含n^(n-2)颗生成树。

生成树的属性：①一个连通图可以有多个生成树

②一个连通图的所有生成树都包含相同的顶点个数和边数

③生成树中不存在环

④移出生成树中的任意一条边都会导致图的不连通

⑤生成树中添加一条边会构成环

⑥对于包含n个顶点的连通图，生成树包含n个顶点和n-1条边

⑦对于n个顶点的无向完全图最多包括n^(n-2)颗生成树

求无向图的生成树

function SpaningTree = stp(G)
    n = size(G,1);
    SpaningTree = size(n,n);
    visited = false(1,n);
    visited(1) = true;%´ÓµÚÒ»¸ö½Úµã¿ªÊ¼±éÀú
    
    for i=2:n
       neighbors = find(G(visited,i) & ~visited(i));
       if ~isempty(neighbors)
           neighbor = neighbors(1);
           SpanningTree(neighbor,i) = 1;
           SpanningTree(i,neighbor) = 1;
           visited(i) = true;
           SpanningTree
           
       else
           error('ͼ²»Á¬Í¨');
       end
    end
end

 

求有向图的生成树

        有向图的生成树要求网络是强联通的，否则只能求出森林而非生成树

        强连通图：图中任意一对顶点之间都存在相互的路径

        代码与上面相似，不置回路

最小生成树

        若在图中考虑权值，也就是在加权连通图G中，生成树的权值定义为生成树中所有边上的权值总合。权值最小的生成树称为该图的最小生成树

        Kruskal算法

        以边为基础，先将边从小到大排列，从小到大不断地添加不构成[环路]的边

        掌握找最小生成树的过程

        Prim算法

        找出已

顶点为基础的下一个权值最小的边，边不指向已连接的节点

        掌握找最小生成树的过程

决策树

        机器学习中的常用的分类算法，树形结构主要由结点和子树构成。结点又分为根节点、内部节点和叶节点

        每一个根节点和内部节点一般是二叉树，向下构造左子树和右子树，构造子树的过程也是将结点数据划分成两个子集

二分图

定义：一个图的顶点集V可分割为两个互不相交的子集(A,B)，并且每条边所关联的两个顶点i和j分别属于这两个不同的顶点集，则称图G是一个二分图

二分图的判断方法：至少有两个顶点，且所有回路的长度均为偶数，任何无回路的图均是二分图（树就是二分图）

二分图的判断方法（染色法）：对节点逐个遍历，然后依次染色

function is_birate = test(G)
    n = size(G,1);%判断节点个数
    is_birate = false;
    col = zeros(1,n);
    for i = 1:n
        if ~col(i) & ~is_birate_bfs(G,i,col)
            is_birate = false;
            return;
        end
    end
    is_birate = true;
end

function result = is_birate_bfs(G,u,col)
    %G图的邻接矩阵
    %u从u节点开始遍历（BFS）
    %col颜色数组
    result = false;
    n = size(G,1);%节点个数

    Queue = u;
    col(u) = 1;%初始化颜色数组
    while ~isempty(Queue)
       head = Queue(1);
       Queue = Queue(2:end);
       %遍历寻找出队节点的邻接节点
       neighbors = find(G(head,:));
       for neighbor = neighbors
                if col(neighbor) == 0
                    col(neighbor) = -col(head);
                    Queue = [Queue,neighbor];
                elseif col(neighbor) == col(head)
                    result = false;
                    return;
                end
       end
    end
    result = true; 
end

二分图最大匹配

        匹配的定义：给定一个二分图G，在G的一个子图M中，任意两条边都不依附于同一个顶点，则称M是一个匹配

       极大匹配、最大匹配、完全匹配都不是唯一的

       极大匹配：在当前已完成的匹配下，无法再通过增加未完成匹配的边的方式来增加匹配的边数

       最大匹配：所有极大匹配当中边数最大的一个匹配，选择这样边数最大的子集称为图的最大匹配问题

        完全匹配：一个匹配当中，图中的每个顶点都和图中某条边相关联

        交替路径：从未分配的节点开始——>未匹配边——>匹配边

        增广路径：未分配节点开始——>交错路径——>未分配节点，这样的一条路径称为增广路径

        增广路径取反，有匹配的路径增多

        匈牙利算法：寻找一组最大匹配，而非所有最大匹配

        寻找最大匹配：

        依次访问左侧的每个节点，搜索以当前节点为起点的任意一条增光路径。如果搜索到增光路径，则将增广路径取反，更新匹配；如果未搜索到则套效果当前节点，直到遍历完所有左侧节点

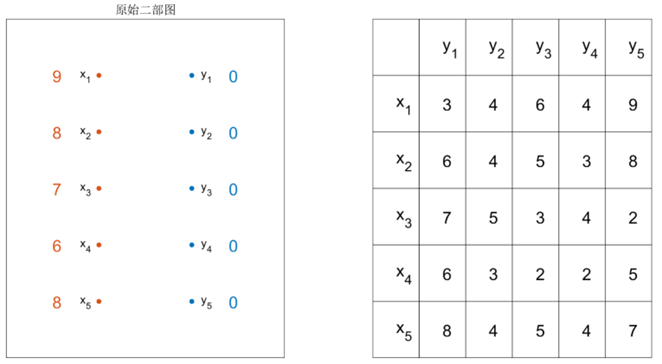
       最大权值匹配：KM算法

        要求能够根据给出最大权重匹配的邻接矩阵，每一步骤具体的操作是怎样的，为什么要减一，减的是哪一列

        不断竞标的过程每个人都只能选择各自权重最高的点。

        如果节点不一致，即8台车匹配9位顾客，此时需要添加虚拟节点补差数，设置连接权重为一个特别小的值使其不会对正常的匹配产生影响

        应用场景：在线广告分配问题，多目标追踪

        KM寻找过程的矩阵变化（掌握每一步矩阵的变化）