有三根杆子(通常称为 A、B 和 C),其中一根杆子A上有一些大小不等的圆盘,按从大到小的顺序依次叠放。我们的任务是将这些圆盘移动到另一根杆子C上,同时满足以下约束条件:
- 每次只能移动一个圆盘。
- 圆盘必须从一个杆子移到另一个杆子。
- 在任何时候,较大的圆盘不能放在较小的圆盘之上。

从这张图片不难看出,移动 3 个盘子需要 7 步,至于是不是最少的次数,大家可以思考一下。(会在下面的内容有所解释)
通过找规律:移动 1、2、3、4 个盘子,分别需要1、3、7、15 步。从而不难猜测移动n个盘子需要2n−1步。
根据游戏规则:
在移动的过程中,我们可以观察移动的步骤,得到一些启发

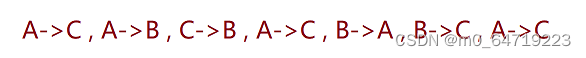
以三个盘子为例,在移动的过程中,我们可以发现其大致的过程是先将小的两个盘子先移动到B杆上,随后直接移动最大的盘子到C杆上,再接着将两个小盘子移动到C杆上。由此,可以将汉诺塔问题转化为一个递归问题:将前N-1个盘子先移动到辅助杆上,再将最大的盘子移动到目标杆上,再递归的将N-1个盘子重复上述过程,直到移动完成。
汉诺塔的基本规则就是移动盘子,则先定义移动盘子的函数:
move(Start, End) :-
write('Move disk '),
write(Start),
write(' -> '),
write(End),
nl.
解决三杆汉诺塔的基本思路如下:
1.对于N个盘子,我们可以将问题分解为两个子问题:
①将前N-1个盘子从A杆移动到B杆,以C杆作为辅助杆。
②将第N个盘子从A杆移动到C杆,移动步数为1的最优子结构。
2.对于子问题1,可以再次递归地将前N-1个盘子从B杆移动到C杆,以A杆作为辅助杆。
3.递归的基本情况:当只有一个盘子时,直接将其从起始杆移动到目标杆。
其基本的思想,就是每次移动都尽可能的利用辅助杆。
将上面的解题思路翻译至prolog语言,可以得到以下的代码:
%汉诺塔3杆问题
hanoi3(N) :-
hanoi3(N, 'A', 'B', 'C').
hanoi3(1, A, _, C) :-
move(A, C).
hanoi3(N, A, B, C) :-
M is N - 1, %取出前n-1个盘子
hanoi3(M, A, C, B), %将A杆上的前n-1个盘子通过C杆移动到B杆
move(A, C), %将A杆的最大盘子移动到C杆(最优子结构)
hanoi3(M, B, A, C). %将B杆上的盘子通过A杆移动到C杆
在移动了前n-1个盘子之后,再将剩余的盘子移动到目标杆,在这里定义为最优子结构,即使用最少的步骤完成一个任务。
这样,汉诺塔3杆的问题就得到了解决。
汉诺塔三杆三个盘子的解:

在与之前的过程相对比,不难发现移动的步骤是一致的。
汉诺塔三杆五个盘子的解:

那么当汉诺塔的杆数增加时,该怎么办?
依葫芦画瓢,我们借用解决3杆问题的步骤和最优子结构的思路:
此时汉诺塔的杆数为4
1.对于N个盘子,我们可以将问题分解为两个子问题:
①将前N-2个盘子从A杆移动到B杆,以C、D杆作为辅助杆。
②将A杆剩余的大盘子通过C杆的辅助移动到D杆,一共三次移动的最优子结构。
2.对于子问题1,可以再次递归地将前N-2个盘子从B杆移动到D杆,以A、C杆作为辅助杆。
3.递归的基本情况:当只有一个盘子时,直接将其从起始杆移动到目标杆。
4.增加的递归的边界条件是N-2等于0时,即杆上有0个盘子,此时不需要做任何的操作。
那么将上述的思路翻译成prolog语言,可以得到如下的代码:
%汉诺塔4杆问题
hanoi4(N) :-
hanoi4(N,'A','B','C','D').
hanoi4(1,A,_,_,D) :- move(A,D).
hanoi4(0,_,_,_,_). %边界条件
hanoi4(N,A,B,C,D) :-
M is N - 2, %取出前n-2个盘子
hanoi4(M,A,C,D,B), %将A杆前n-2个盘子通过C、D杆移动到B杆
move(A,C), %此时将A杆上面的最小的盘子移动到C杆
move(A,D), %将A杆上剩余的最大的一个盘子移动到D杆
move(C,D), %将C杆上的第二大的盘子移动到D杆
hanoi4(M,B,A,C,D). %将B杆上的n-2个盘子通过A、C杆移动到D杆上
在以上代码的运行下,可以得到汉诺塔4杆问题的解。
借助于汉诺塔4杆的解决思路
当汉诺塔的杆数为5时,同样的思路:
1.对于N个盘子,我们可以将问题分解为两个子问题:
①将前N-3个盘子从A杆移动到B杆,以C、D、E杆作为辅助杆。
②将A杆剩余的大盘子通过C、D杆的辅助移动到E杆,一共四次移动的最优子结构。
2.对于子问题1,可以再次递归地将前N-3个盘子从B杆移动到E杆,以A、C、D杆作为辅助杆。
3.递归的基本情况:当只有一个盘子时,直接将其从起始杆移动到目标杆。
4.递归的边界条件是N-3等于0时,即杆上有0个盘子,此时不需要做任何的操作。
5.新增加的递归的边界条件是A杆上的盘子只有两个时,此时通过C、D、E杆的辅助,共移动三次,到达B杆。
将上述的思路翻译为prolog语言,得到如下代码:
%汉诺塔5杆问题
hanoi5(N) :-
hanoi5(N,'A','B','C','D','E').
hanoi5(0,_,_,_,_,_).
hanoi5(1,A,_,_,_,E) :- move(A,E).
hanoi5(2,A,C,D,E,B) :- %当A杆上只有两个盘子时,通过C、D、E杆的辅助,移动三次,到达B杆上
move(A,C),
move(A,B),
move(C,B).
hanoi5(N,A,B,C,D,E) :-
M is N - 3,
hanoi5(M,A,C,D,E,B), %将前n-3个盘子通过C、D、E移动到B杆上
%将A杆上剩余三个盘子通过C、D杆的辅助,最少次数移动到E杆
move(A,C),
move(A,D),
move(A,E),
move(D,E),
move(C,E),
hanoi5(M,B,A,C,D,E). %将B杆上的n-3个盘子通过A、C、D杆的辅助,移动到E杆上
prolog验证:
当盘子数量为4时:
在汉诺塔3杆上的移动步骤:

在汉诺塔4杆上的移动步骤:
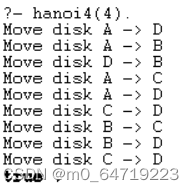
在汉诺塔5杆上的移动步骤:

首先,需要验证其步骤的正确性:
因为条件的局限性,不能使得其过程可视化,所以,在当前的情况下,使用瞪眼法加想象法。可以验证,该步骤是正确的。
其次,比较使用不同杆移动的次数:
通过对比可以发现,盘子数量为4时:
在汉诺塔3杆上的移动次数为15次
在汉诺塔4杆上的移动次数为9次
在汉诺塔5杆上的移动次数为7次
经过分析可以得知,当盘子数量n等于杆的数量减1时,在遵守游戏规则的情况下,最少的移动次数为2n-1次。
显然,上面的结果是合法的,且已经达到了最优的移动次数。
通过理论分析可以得知,要在汉诺塔多杆问题中求解,且使得移动次数最少化,那么就要充分的利用辅助杆,即空闲的、可移动的杆。
在上面的规律下不难看出,要使得优解且移动次数最小化,可以推广到n杆的操作:设杆数量为t,盘子数量为n,则先将A杆的前n-(t-2)个盘子通过t-2个辅助杆移动到B杆上,然后将A杆上的t-2个盘子使用最优子结构通过t-2个辅助杆移动到目标杆上(每个盘子移动到不同的辅助杆,保证其中最大的盘子移动到目标杆,再移动辅助杆上盘子至目标杆),可以验证这一操作的移动次数是最少的,然后将A杆看做B杆,B杆看作A杆,递归的重复上述步骤,可得到最优解。
在prolog的实现中,需要额外的定义t-2个边界条件,其分别是从盘子数n等于0开始,到n等于t-2-1结束,每个边界条件里面都要使用最优子结构,这是必要的,保证移动次数最少。
当A杆上的盘子数量大于t-2时,通过最优子结构的最少次数移动较大的盘子到目标杆上;否则直接使用定义的边界条件谓词。
分解子问题:
Step1:首先将A杆上n-(t-2)个盘子都尽可能的先移动到B杆;
Step2:将A杆剩余的t-2个盘子经过最少次步数移动到目标杆;
Step3:再将B杆看作A杆,A杆看作B杆;
Step4:当A杆上盘子数量大于t-2时,返回Step1;否则直接最少次数移动盘子到目标杆上
经过有限次的步骤,可以得到最后的解。
最后附上完整的prolog代码:
%汉诺塔3杆问题
hanoi3(N) :-
hanoi3(N, 'A', 'B', 'C').
hanoi3(1, A, _, C) :-
move(A, C).
hanoi3(N, A, B, C) :-
M is N - 1, %取出前n-1个盘子
hanoi3(M, A, C, B), %将A杆上的前n-1个盘子通过C杆移动到B杆
move(A, C), %将A杆的最大盘子移动到C杆
hanoi3(M, B, A, C). %将B杆上的盘子通过A杆移动到C杆
move(Start, End) :-
write('Move disk '),
write(Start),
write(' -> '),
write(End),
nl.
%汉诺塔4杆问题
hanoi4(N) :-
hanoi4(N,'A','B','C','D').
hanoi4(1,A,_,_,D) :- move(A,D).
hanoi4(0,_,_,_,_).
hanoi4(N,A,B,C,D) :-
M is N - 2, %取出前n-2个盘子
hanoi4(M,A,C,D,B), %将A杆前n-2个盘子通过C、D杆移动到B杆
move(A,C), %此时将A杆上面的最小的盘子移动到C杆
move(A,D), %将A杆上剩余的最大的一个盘子移动到D杆
move(C,D), %将C杆上的第二大的盘子移动到D杆
hanoi4(M,B,A,C,D). %将B杆上的n-2个盘子通过A、C杆移动到D杆上
%汉诺塔5杆问题
hanoi5(N) :-
hanoi5(N,'A','B','C','D','E').
hanoi5(0,_,_,_,_,_).
hanoi5(1,A,_,_,_,E) :- move(A,E).
hanoi5(2,A,C,D,E,B) :- %当A杆上只有两个盘子时,通过C、D、E杆的辅助,移动三次,到达B杆上
move(A,C),
move(A,B),
move(C,B).
hanoi5(N,A,B,C,D,E) :-
M is N - 3,
hanoi5(M,A,C,D,E,B), %将前n-3个盘子通过C、D、E移动到B杆上
%将A杆上剩余的三个盘子通过C、D杆的辅助,移动到E杆上
move(A,C),
move(A,D),
move(A,E),
move(D,E),
move(C,E),
hanoi5(M,B,A,C,D,E). %将B杆上的n-3个盘子通过A、C、D杆的辅助,移动到E杆上





















 1473
1473











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








