变异系数

公式

一行表示变异系数的计算公式：变异系数 C·V =（ 标准偏差 SD / 平均值Mean ）× 100%

注意：是标准差的无偏估计【除以（n-1）的那个】再除以均值。
有时候也乘100，表示为百分数，好看。就这个：

使用注意

变异系数只对由比率标量计算出来的数值有意义。举例来说，对于一个气温的分布，使用开尔文或摄氏度来计算的话并不会改变标准差的值，但是温度的平均值会改变，因此使用不同的温标的话得出的变异系数是不同的。也就是说，使用区间标量得到的变异系数是没有意义的。

变异系数的作用

变异系数（Coefficient of Variation）：当需要比较两组数据离散程度大小的时候，如果两组数据的测量尺度相差太大，或者数据量纲的不同，直接使用标准差来进行比较不合适，此时就应当消除测量尺度和量纲的影响，而变异系数可以做到这一点，它是原始数据标准差与原始数据平均数的比。CV没有量纲，这样就可以进行客观比较了。事实上，可以认为变异系数和极差、标准差和方差一样，都是反映数据离散程度的绝对值。其数据大小不仅受变量值离散程度的影响，而且还受变量值平均水平大小的影响。

优点

比起标准差来，变异系数的好处是不需要参照数据的平均值。变异系数是一个无量纲量，因此在比较两组量纲不同或均值不同的数据时，应该用变异系数而不是标准差来作为比较的参考。

缺点

1、当平均值接近于0的时候，微小的扰动也会对变异系数产生巨大影响，因此造成精确度不足。
2、变异系数无法发展出类似于均值的置信区间的工具（详见问题导航）。

问题导航

想了解变异系数为什么不能发展类似于均值的置信区间，需要知道均值的置信区间是什么；
而要知道均值的置信区间，就要先了解置信区间的概念；
置信区间的概念：问题1
均值的置信区间：问题2
变异系数为什么没有似于均值的置信区间：问题3

问题1

置信区间是建立在点估计的基础上，让我们先用5秒了解点估计：

点估计

在点估计的基础上，在一定的置信水平下，给样本统计量加上一个区间范围作为总体参数的取值范围，这个区间叫置信区间。
简单通俗地讲一下两者之间的关系：

是不是又不懂什么是置信水平了？（这个解释写的是真的好）

置信水平

为什么他用95%举例？


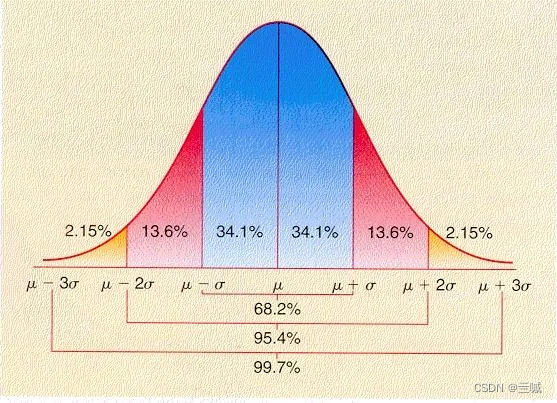
同时这也是显著性水平a取0.05的原因。

置信区间的特点

问题2

主要涉及到求均值的置信区间的公式：

至于这个公式怎么来的就别难为我了。

问题3

我给自己找了一个难题，全网只有一个提问的，还没有答案。
下面是提问者的理解：

而我个人认为置信区间是一个范围，是一种概率的体现；
而变异系数是一个具体的数，没有范围和概率一说。（而且我认为变异系数太吃测试数据曲线了，有种过拟合的感觉，换一些数据就直接改变结果。）有错误请@我。

个人小结

有一说一，虽然之前没听过，但变异系数的应用范围是真的广。

文章来源

来源1
来源2
来源3
来源4
来源5
来源6