底层运动控制算法及代码实现（学习笔记二）

一、PID控制算法

PID控制律：

误差：

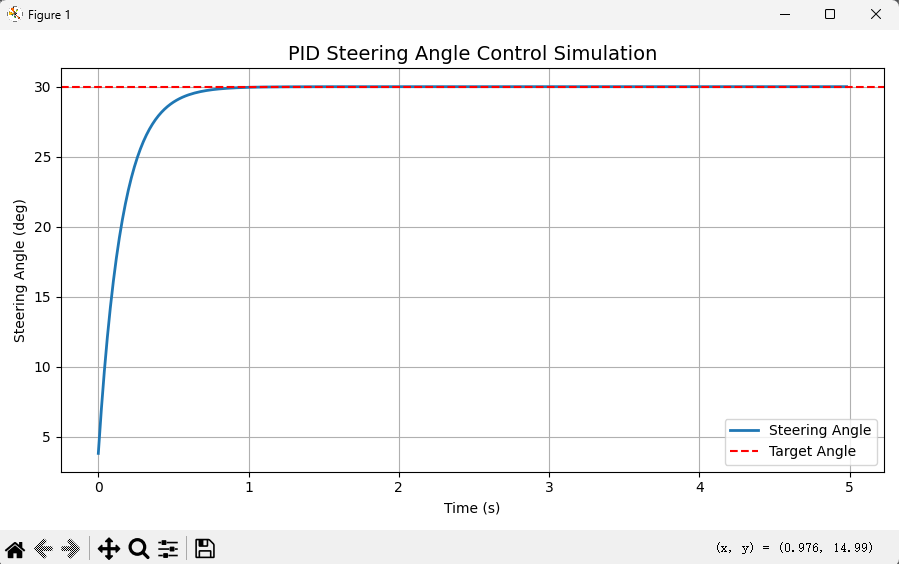
任务场景：小车转向角从0到30

import numpy as np
import matplotlib.pyplot as plt


# ---------------- PID 控制器 ----------------
class PositionPID:
    def __init__(self, Kp, Ki, Kd, setpoint=0):
        self.Kp = Kp
        self.Ki = Ki
        self.Kd = Kd
        self.setpoint = setpoint

        self.integral = 0  # 积分累计值
        self.prev_error = 0   # 上一次误差

    def update(self, measurement, dt):
        error = self.setpoint - measurement
        self.integral += error * dt
        # 微分 =（当前误差 - 上次误差）/ 时间间隔
        derivative = (error - self.prev_error) / dt if dt > 0 else 0
        self.prev_error = error

        return (
                self.Kp * error +
                self.Ki * self.integral +
                self.Kd * derivative
        )


# ---------------- 小车转向角模拟(应用场景) ----------------
dt = 0.02  # 控制周期
time = np.arange(0, 5, dt)  # 模拟 5 秒

target_angle = 30  # 目标转向角度（度）
pid = PositionPID(Kp=8.0, Ki=0.01, Kd=0.01, setpoint=target_angle)

angle = 0  # 初始方向角
angles = []
outputs = []

for t in time:
    u = pid.update(angle, dt)  # PID 输出
    angle += u * 0.015  # 小车转向响应模型（简化）

    angles.append(angle)
    outputs.append(u)

# -------------------- 画图 --------------------
plt.figure(figsize=(9, 5))
plt.plot(time, angles, label="Steering Angle", linewidth=2)
plt.axhline(target_angle, color='r', linestyle='--', label="Target Angle")

plt.title("PID Steering Angle Control Simulation", fontsize=14)
plt.xlabel("Time (s)")
plt.ylabel("Steering Angle (deg)")
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()

二、LQR（Linear Quadratic Regulator）：线性二次型最优状态反馈

 对于二维离散线性系统，系统形式如下：

选择一个简单系统（位置-速度二阶系统）：

系统模型建立：

import numpy as np
import matplotlib.pyplot as plt

A = np.array([[1, 0.1],
              [0, 1   ]])

B = np.array([[0],
              [0.1]])

def plant_update(x, u):
    return A @ x + B * u

LQR算法实现：

代价函数权重自定义：

# ===================
# 选择代价函数权重
# ===================
Q = np.diag([10, 1])    # 惩罚位置误差 > 速度误差
R = np.array([[1]])     # 惩罚控制输入

迭代法求解方程

得到K

# ===================
# 求解离散 Riccati 方程
# ===================
P = Q.copy()
for _ in range(200):
    P = Q + A.T @ P @ A - A.T @ P @ B @ np.linalg.inv(R + B.T @ P @ B) @ B.T @ P @ A

# 最优反馈增益
K = np.linalg.inv(R + B.T @ P @ B) @ B.T @ P @ A
K = K.reshape(1, 2)
print("LQR Feedback Gain K =", K)

# ===================
# LQR 跟踪控制律：u = -K(x - x_ref)
# ===================
def lqr_control(x, r):
    x_ref = np.array([[r], [0]])   # 参考位置 = r，速度=0
    return (-K @ (x - x_ref))[0, 0]


# ===================
# 仿真
# ===================
steps = 50
r = 1.0  # 目标位置

x = np.array([[0.0], [0.0]])
history = []

def plant_update(x, u):
    return A @ x + B * u

for _ in range(steps):
    u = lqr_control(x, r)
    x = plant_update(x, u)
    history.append(x[0,0])

# ===================
# 绘图
# ===================
plt.plot(history, label="LQR")
plt.axhline(r, linestyle="--", color="gray", label="Reference r=1")
plt.title("LQR Tracking Control on 2D System")
plt.xlabel("Step")
plt.ylabel("x1 (Position)")
plt.grid(True)
plt.legend()
plt.show()

三、模型预测控制（MPC）

参考：https://blog.csdn.net/qq_44940689/article/details/139808413