贝叶斯分类器

你的凡王

已于 2024-05-30 12:03:24 修改

阅读量250

点赞数 7

文章标签：机器学习

于 2024-05-28 20:14:02 首次发布

本文链接：https://blog.csdn.net/m0_65325092/article/details/139276900

版权

贝叶斯决策论

概率论框架下实施决策的基本方法，对分类任务来说，在所有相关概率都已知的情况下，贝叶斯决策论考虑如何基于这些概率与误判损失来选择最优类别标记。

假设有N种可能得类别标记，即

$\mathfrak{Y}=\{c_1,...,c_N\},$

λ_ij是将真实类别为c_j误分类为c_i产生的损失，若有后验概率P(c_j|x)，则将样本x分类为c_j产生的期望损失为

$R(c_i|\vec{x})=\sum\limits_{j=1}^{N}\lambda_{ij}P(c_j|\vec{x}),$

(注意自变量x处因变量取什么类别是一个概率，而非定值)。我们希望寻求一个判定准则

$h:\mathfrak{X} \mapsto \mathfrak{Y}$

使得风险

$R(h)=\mathbb{E}_{\vec{x}}[R(h(\vec{x})|\vec{x})]$

最小。

显然若对任意x，决策h都能使得R(h(x)|x)最小化，则R(h)也会被最小化，这就是贝叶斯然定准则，即取

$h^*(\vec{x})=\mathop{\mathrm{arg\;min}} \limits_{c\in \mathfrak{Y}} R(c|\vec{x}), \;\; \forall \vec{x},$

h*称为贝叶斯最优分类器，R(h*)称为贝叶斯风险，1-R(h*)为分类器的最佳性能，是模型精度的理论上限。

对分类问题，我们取

$\lambda_{ij} = \left\{\begin{matrix} 0,\;\;i=j,\\ 1,\;\;i \neq j. \end{matrix}\right.$

此时

$R(c_i|\vec{x})=\sum\limits_{j\neq i} P(c_j|\vec{x}) = 1-P(c_i|\vec{x}),$

由此可得贝叶斯分类器

$h^*(\vec{x})=\mathop{\mathrm{arg\;min}} \limits_{c\in \mathfrak{Y}} (1-P(c|\vec{x}))=\mathop{\mathrm{arg\;max}} \limits_{c\in \mathfrak{Y}} P(c|\vec{x}), \;\; \forall \vec{x},$

即直接选择后验概率最大的类别，因此问题就被转化成了求后验概率P(c|x)，由贝叶斯公式可知

$P(c|\vec{x})=\frac{P(c)P(\vec{x}|c)}{P(\vec{x})},$

由于我们是关于c求最大值，因此上式分子可以直接舍弃。问题转化为求P(c)和P(x|c)。前者我们是能够观测到的，直接将观测样本中类别c出现的比例作为P(c)，对于后者，可将类别为c的样本子集中自变量取x的样本点占比作为P(x|c)。即，假设样本D中类别为c的子集为D_c，D_c中x=x_i的子集为D_c,x_i，则

$P(c)=\frac{|D_c|}{|D|},\;\;P(\vec{x}=\vec{a}|c)=\frac{|D_{c,\vec{a}}|}{|D_c|}.$

以上为非参数方法。然而由于我们需要得到x所有可能的取值下的后验概率，当特征向量x的维数较高时，x可能的取值会极多，与之相比样本量是较少的，这就使得估计P(x|c)所需的样本要么极少要么根本没有。解决这一问题的方法包括假设自变量总体的概率分布P(x|c)形式已知(如正态分布、伽马分布等)，然后通过最大似然方法估计出总体分布的未知参数从而得到总体概率分布P(x|c)，但是此方法的准确性严重依赖所假设的概率分布是否与真实分布相符。此外也可以用下一节中的朴素贝叶斯分类器在引入额外假设的情况下使用上面的非参数方法。

朴素贝叶斯分类器

我们添加特征(属性)条件独立性假设，假设同属于一个类别的各个属性是相互独立的，即

$P(\vec{x}|c)=\prod\limits_{j=1}^{d}P(x^{(j)}|c),\;\;\forall c.$

其中x_j是x的第j个分量，d是x的维数。我们有

$P(c)=\frac{|D_c|}{|D|},\;\;P(x^{(j)}=a|c)=\frac{|D_{c,x^{(j)}=a}|}{|D_c|}.$

$P(c)=\frac{|D_c|+1}{|D|+N},\;\;P(x^{(j)}=a|c)=\frac{|D_{c,x^{(j)}=a}|+1}{|D_c|+N^{(j)}}.$

贝叶斯网

贝叶斯网B由结构G和参数Θ构成，记为B=(G, Θ)，网络结构G是一个有向无环图，每个节点代表一个属性(自变量或因变量)，若两个变量有直接依赖关系，则它们由一条边连接起来，参数Θ定量描述这种依赖关系，假设两个属性有直接依赖关系，则二者之间有一条边相连，Θ包含属性与其子结点之间的条件概率。

结构

贝叶斯网络表达了属性间的条件独立性，给定父结点的条件下任意属性与其非后代属性独立，因此B中联合概率分布为

$P(x^{(1)},...,x^{(m)})=\prod\limits_{j=1}^{m}P(x^{(j)}|\pi^{(j)}),$

这里假设考虑的变量一共m个，包括自变量因变量，π表示父结点，可以是一个变量，也可以是多个变量，也可以是0个变量(即无条件概率)。

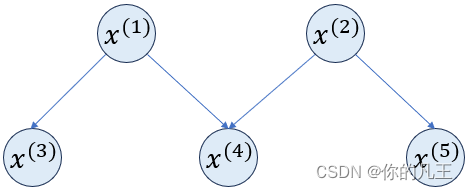
以上图为例，x(3)和x(4)在给定x(1)的取值时独立。它们的联合概率为

$P(x^{(1)},...,x^{(5)})=P(x^{(1)})P(x^{(2)})P(x^{(3)}|x^{(1)})P(x^{(4)}|x^{(1)},x^{(2)})P(x^{(5)}|x^{(2)}).$

学习

首先需要通过训练数据集找出最为恰当的贝叶斯网结构，常用方法为评分搜索，首先定义一个评分函数，评估贝叶斯网与训练数据的契合程度，然后基于评分函数求出最优结构。常用评分函数通常基于信息论准则，目标是找到一个能以最短编码长度描述训练数据的模型。训练数据集为

$D=\{\vec{x}_1,...,\vec{x}_m\},$

贝叶斯网B=(G, Θ)，在D上的评分函数为

$s(B|D)=f(\theta)|B|-LL(B|D),$

其中|B|是贝叶斯网的参数个数，f(θ)是描述每个参数θ所需的编码位数，

$LL(B|D)=\sum\limits_{i=1}^{m}\textup{log}P(\vec{x}_i),$

是贝叶斯网的对数似然。我们所求的网络结构应当使得s(B|D)最小。f(θ)=1时s(B|D)是AIC评分函数，f(θ)=½logm时s(B|D)是BIC评分函数。固定网络结构后，s(B|D)就变成了最大似然估计问题，其中的P(x)的形式通过上一小节的公式可以写出。然而从所有可能的网络结构中搜索出最优结构是一个NP难问题，无法快速求解，常用策略是贪心法和对网络结构施加约束，前者从某个网络结构出发，每次调整一条边(增、删、改变方向)，直到s(B|D)不再降低，后者在施加约束条件后能将搜索空间减小，例如可将网络结构限定为树形。

推断

得到训练好的贝叶斯网后可以回答查询问题，即通过一列属性变量的观测值来推测其他属性变量取值，理想情况是根据贝叶斯网定义的联合概率分布来精确计算后验概率，不幸的是这种精确推断是NP难得到，当网络节点较多、连接稠密时难以进行精确推断，此时需要使用近似推断，降低精确度来短时间内求出近似解。近似推断常常通过Gibbs抽样进行。

令

$\vec{Q}=\{Q^{(1)},...,Q^{(n)}\}$