绪论
数据结构是相互之间存在一种或多种特定关系的数据元素的集合
通常有四种基本结构:
(1)集合
(2)线性结构
(3)树形结构
(4)图状结构或网状结构
结构定义中的“关系”描述的是数据元素之间的逻辑关系,因此又被称为数据的逻辑结构
数据结构在计算机中的表示(又称映像)称为数据的物理结构,又称存储结构。存储结构又分为顺序存储结构和链式存储结构。
抽象数据类型(Abstract Data Type 简称ADT)是指一个数学模型以及定义在此数学模型上的一组操作。抽象数据类型需要通过固有数据类型(高级编程语言中已实现的数据类型)来实现。抽象数据类型是与表示无关的数据类型,是一个数据模型及定义在该模型上的一组运算。对一个抽象数据类型进行定义时,必须给出它的名字及各运算的运算符名,即函数名,并且规定这些函数的参数性质。一旦定义了一个抽象数据类型及具体实现,程序设计中就可以像使用基本数据类型那样,十分方便地使用抽象数据类型。
算法是在有限步骤内求解某一问题所使用的一组定义明确的规则。通俗点说,就是计算解题的过程。在这个过程中,无论是形成解题思路还是编写程序,都是在实施某种算法。前者是推理实现的算法,后者是操作实现的算法。
一个算法应该具有以下五个重要的特征:
1、有穷性: 一个算法必须保证执行有限步之后结束;
2、确切性: 算法的每一步骤必须有确切的定义;
3、输入:一个算法有0个或多个输入,以刻画运算对象的初始情况,所谓0个输入是指算法本身定除了初始条件;
4、输出:一个算法有一个或多个输出,以反映对输入数据加工后的结果。没有输出的算法是毫无意义的;
5、可行性: 算法原则上能够精确地运行,而且人们用笔和纸做有限次运算后即可完成。
一般情况下,算法的基本操作重复执行的次数是模块n的某一个函数f(n),因此,算法的时间复杂度记做:T(n)=O(f(n))
分析:随着模块n的增大,算法执行的时间的增长率和 f(n) 的增长率成正比,所以 f(n) 越小,算法的时间复杂度越低,算法的效率越高。
2. 在计算时间复杂度的时候,先找出算法的基本操作,然后根据相应的各语句确定它的执行次数,再找出 T(n) 的同数量级(它的同数量级有以下:1,log(2)n,n,n log(2)n ,n的平方,n的三次方,2的n次方,n!),找出后,f(n) = 该数量级,若 T(n)/f(n) 求极限可得到一常数c,则时间复杂度T(n) = O(f(n))
空间复杂度(Space Complexity):
1:空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度;
2:一个算法在计算机上占用的内存包括:程序代码所占用的空间,输入输出数据所占用的空间,辅助变量所占用的空间这三个方面,程序代码所占用的空间取决于算法本身的长短,输入输出数据所占用的空间取决于要解决的问题,是通过参数表调用函数传递而来,只有辅助变量是算法运行过程中临时占用的存储空间,与空间复杂度相关;
3:通常来说,只要算法不涉及到动态分配的空间,以及递归、栈所需的空间,空间复杂度通常为0(1);
4: 对于一个算法,其时间复杂度和空间复杂度往往是相互影响的。当追求一个较好的时间复杂度时,可能会使空间复杂度的性能变差,即可能导致占用较多的存储空间;反之,求一个较好的空间复杂度时,可能会使时间复杂度的性能变差,即可能导致占用较长的运行时间。另外,算法的所有性能之间都存在着或多或少的相互影响。因此,当设计一个算法(特别是大型算法)时,要综合考虑算法的各项性能,算法的使用频率,算法处理的数据量的大小,算法描述语言的特性,算法运行的机器系统环境等各方面因素,才能够设计出比较好的算法。
线性表是最基本、最简单、也是最常用的一种数据结构。
线性表中数据元素之间的关系是一对一的关系,即除了第一个和最后一个数据元素之外,其它数据元素都是首尾相接的(注意,这句话只适用大部分线性表,而不是全部。比如,循环链表逻辑层次上也是一种线性表(存储层次上属于链式存储),但是把最后一个数据元素的尾指针指向了首位结点)。
线性表
线性表一般包含如下几种操作:
线性表的操作包括如下几种
(1) InitList(& L)
//构造一个空的线性表
(2) DestroyList(& L)
//线性表存在了,消耗一个线性表
(3) ClearList(&L )
//清空线性表中的内容
(4) ListEmpty(L)
//判断线性表是否为空
(5) ListLength(L)
//返回线性表的长度
(6) GetElem(L,i,& e)
//返回线性表i位置上的元素值,通过e返回
(7) PriorElem(L,cur_e,&pre_e)
//如果cur_e是线性表中的元素,而且不是第一个,那么我们就可以返回该元素前一个元素的值
(8) NextElem(L,cur_e,&next_e)
//如果cur_e是线性表中的元素,而且不是最后一个,就返回它下一个元素的值
(9) Listinsert(&L,i,e)
//如果线性表存在了,而且i符合条件,则在i位置插入一个元素
(10)ListDelete(&L,i)
//删除i位置上的元素
(11) ListDelete_data(&L,e,order)
//删除指定的元素e,order决定是删除一个,还是全部。
(12) Connect_two_List(L_a,L_b,& L_c)
//连接两个线性表,除去重复的内容
(13)print(L)
//打印线性表 线性表的顺序表示实现–表示的格式
我们在之后的那些操作的实现中,我们都是一直使用这些内容,作为我们通过线性表顺序结构表示实现线性表操作的一些基础。
//扩充容量的步伐
#define sizestep 10
//开始的容量的大小
#define startsize 100
//为了便于扩展,我们这里使用类型别名,
//我们使用最简单的int型作为一个范例
typedef int Elemtype;
struct List {
//数据
Elemtype * data;
//长度
int length;
//初始容量
int size;
};
线性表顺序表示实现–initList函数
因为顺序表示就是对数组进行一些操作,我们在第四点已经给出了我们顺序表示线性表的一个结构体,我们要创建一个空表(没有元素的表),我们就是让表的长度为0,另外,还要对data进行堆内存的分配和初始容量的初始化。
//创建一个空的线性表
void InitList(List & newList) {
//初始容量为startsize
newList.size = startsize;
//首先开辟空间
newList.data = new Elemtype[newList.size];
//空表,长度是0
newList.length = 0;
}
线性表顺序表示实现–DestroyList函数
//线性表存在了,现在要销毁线性表
void DestroyList(List & newList) {
newList.length = 0;
newList.data = 0;
//一定要先释放堆内存
delete[] newList.data;
//没此释放堆内存后,并将对应的指针赋予NULL是一个良好的习惯
newList.data = NULL;
}
线性表顺序表示实现–ClearList函数
//线性表存在了,但是现在想清空整个线性表
void ClearList(List & newList) {
newList.length = 0;
//一定要先释放堆内存
delete[] newList.data;
//没此释放堆内存后,并将对应的指针赋予NULL是一个良好的习惯
newList.data = NULL;
//重新为存放元素的变量开辟一个新的堆内存
newList.data = new Elemtype[newList.size];
}
8、线性表顺序表示实现–ListEmpty函数
//判读线性表是否为空
bool ListEmpty(List newList) {
return newList.length;
}
线性表顺序表示实现–ListLength函数
//返回线性表的长度
int ListLength(List newList) {
return newList.length;
}
线性表顺序表示实现–GetElem函数
//返回线性表上某个位置上的元素的值,记住我们的位置是从1开始计算的。
void GetElem(List newList, int i, Elemtype &e) {
if (ListEmpty(newList)) {
cout << "当前线性表是空表" << endl;
return;
}
if (i<1 || i>newList.length) {
cout << "当前位置超出了线性表的范围" << endl;
return;
}
e = newList.data[i - 1];
}
我们需要考虑这个函数的时间复杂度:因为我们是通过下标进行查找对应的元素的,所以它是时间复杂度为:O(1),这个和我们后边说的链式结构的查找比起来,是占了很大优势的
11、线性表顺序表示实现–PriorElem函数
我们在执行这个函数的第一步就是判断我们的那个元素在不在线性表中且不是第一个元素,这样我们就可以直接返回该元素的前一个元素的值。
//判读元素的位置的函数
//我们这里直接返回该元素的下标
int LocationElem(List newList, Elemtype e){
int i;
for (i = 0; i < newList.length; i++) {
if (newList.data[i] == e) {
return i;
}
}
return -1;
}
这个函数的时间复杂为:假定我们有n个元素,那么它的查找时间复杂为O(n),但是因为我们使用的是顺序结构,所以我们可以很方便的使用其他可以减低时间复杂的查找算法,例如二分查找,它的时间复杂度为:O(logn)
//获取前驱的元素
void PriorElem(List newList, Elemtype cur_e, Elemtype & pre_e) {
int location = 0;
location = LocationElem(newList, cur_e);
//如果Location是-1,说明cur_e不在线性表中
if (location == -1) {
cout <<cur_e<< "不在线性表中" << endl;
return;
}
//如果Location是0,说明cur_e在线性表第一个位置,没有前一个元素
if (location == 0)
{
cout << cur_e << "是线性表的第一个元素,没有前驱" << endl;
return;
}
pre_e = newList.data[location - 1];
}
这个函数的时间复杂主要是受LocationElem函数的影响,
线性表顺序表示实现–NextElem函数
这个函数和前面的函数是一样的,我们只要修改一个位置的参数就可以了,那就是判断第一个元素的变为判断最后一个元素
//获取后驱元素
void NextElem(List newList, Elemtype cur_e, Elemtype & next_e) {
int location = 0;
location = LocationElem(newList, cur_e);
//如果Location是-1,说明cur_e不在线性表中
if (location == -1) {
cout << cur_e << "不在线性表中" << endl;
return;
}
//如果Location是0,说明cur_e在线性表最后一个位置,没有后一个元素
if (location == newList.length-1)
{
cout << cur_e << "是线性表的最后一个元素,没有后驱" << endl;
return;
}
next_e = newList.data[location - 1];
}
这个函数的时间复杂为
线性表顺序表示实现–Listinsert函数
//向线性表中插入一个元素,这里我们需要判断插入位置是否合法
//除此之外,我们还需要检测元素的容量是否已经到达了最大值
void Listinsert(List & newList, int i, Elemtype e) {
//插入的位置不合法
if (i<1 || i>newList.length+1) {
cout << "请检查插入位置是否正确" << endl;
return;
}
int j = 0;
//此时达到了线性表的最大容量,我们需要重新为线性表分配新的内存。
if (newList.length == newList.size) {
//先保存之前的内容。
Elemtype * p =new Elemtype[newList.length];
for (j = 0; j < newList.length; j++) {
p[j] = newList.data[j];
}
//扩大容量
newList.size += sizestep;
delete[] newList.data;
//重新分配内存
newList.data = new Elemtype[newList.size];
//恢复之前内容
for (j = 0; j < newList.length; j++) {
newList.data[j] = p[j];
}
}
//插入内容
for (int k = newList.length; k >i-1; k-- ){
newList.data[k]=newList.data[k-1];
}
newList.data[i - 1] = e;
++newList.length;
}
线性表的顺序结构表示的时候,它的最大的缺点就是在插入和删除的时候,需要移动大量的元素,此时,我们插入一个元素的时间复杂为:O(n),时间复杂度虽然是线性的,但是由于它需要移动大量的元素,这也就早造成了它的时间效率的比较低的
线性表顺序表示实现–Listdelete函数
//线性表删除一个元素,我们需要判断删除的位置是否合法
void Listdelete(List & newList, int i) {
//删除的位置不合法
if (i<1 || i>newList.length) {
cout << "请检查插入位置是否正确" << endl;
return;
}
for (int j = i - 1; j < newList.length; j++) {
newList.data[j] = newList.data[j + 1];
}
--newList.length;
}
线性表的删除和插入是差不多的意思,都是要对数组中的元素进行移动。
线性表顺序表示实现–Listdelete_data函数
//按照元素的值,来删除对应元素的内容,
//这个时候我们通过传个参数,来决定我们是删除第一个该元素,
//0,删除一个,1,删除所有
//还是把所有的元素都给删除了
//如果不存在该元素,就直接返回
void Listdelete_data(List & newList, Elemtype e,int order) {
int flag=0;
for (int i = 0; i < newList.length; i++) {
if (newList.data[i] == e) {
flag=1;
//删除对应的位置上的元素,而且i也要减少一个
Listdelete(newList, i + 1);
--i;
if (order == 0) {
return;
}
}
}
if(flag==1)
return ;
cout << e << "不在线性表中" << endl;
}
线性表顺序结构表示实现–Connect_two_List函数
当我们要进行两个线性表的链接的时候,我们最好是希望这两个链表是有序的。
//连接两个线性表
void Connect_two_List(List a, List b, List & c) {
//对c进行一些数据初始化
c.length = c.size = a.length + b.length;
c.data = new Elemtype[c.size];
//这里采用指针的方式进行数据的移动,我们先把a和b数据第一个和最后一个元素的位置找出来
int i = 0;
int j = 0;
int k = 0;
while (i <= a.length-1 && j<= b.length-1) {
if (a.data[i] < b.data[j])
{
c.data[k++] = a.data[i++];
}
else if(a.data[i] > b.data[j]) c.data[k++] = b.data[j++];
else {
c.data[k++] = b.data[j++]; i++; --c.length;
}
}
while (i <= a.length - 1)
{
c.data[k++] = a.data[i++];
}
while (j <= b.length - 1)
{
c.data[k++] = b.data[j++];
}
}
我们通过分析我们连接函数的代码,我们可以发现,我们将两个元素组合在一起的时候的时间复杂为O(a.lenght+b.lenght).
17、线性表顺序结构表示实现–print函数
void print(List & L) {
for (int i = 0; i < L.length; i++) {
cout << L.data[i] << " ";
}
cout << endl;
}
链表
是一种常见的基础数据结构,结构体指针在这里得到了充分的利用。链表可以动态的进行存储分配,也就是说,链表是一个功能极为强大的数组,他可以在节点中定义多种数据类型,还可以根据需要随意增添,删除,插入节点。链表都有一个头指针,一般以head来表示,存放的是一个地址。链表中的节点分为两类,头结点和一般节点,头结点是没有数据域的。链表中每个节点都分为两部分,一个数据域,一个是指针域。说到这里你应该就明白了,链表就如同车链子一样,head指向第一个元素:第一个元素又指向第二个元素;……,直到最后一个元素,该元素不再指向其它元素,它称为“表尾”,它的地址部分放一个“NULL”(表示“空地址”),链表到此结束。
作为有强大功能的链表,对他的操作当然有许多,比如:链表的创建,修改,删除,插入,输出,排序,反序,清空链表的元素,求链表的长度等等。
初学链表,一般从单向链表开始
--->NULL
head
这是一个空链表。
---->[p1]---->[p2]...---->[pn]---->[NULL]
head p1->next p2->next pn->next
有n个节点的链表。
创建链表
typedef struct student{
int score;
struct student *next;
} LinkList;
一般创建链表我们都用typedef struct,因为这样定义结构体变量时,我们就可以直接可以用LinkList *a;定义结构体类型变量了。
初始化一个链表,n为链表节点个数。
LinkList *creat(int n){
LinkList *head, *node, *end;//定义头节点,普通节点,尾部节点;
head = (LinkList*)malloc(sizeof(LinkList));//分配地址
end = head; //若是空链表则头尾节点一样
for (int i = 0; i < n; i++) {
node = (LinkList*)malloc(sizeof(LinkList));
scanf("%d", &node->score);
end->next = node;
end = node;
}
end->next = NULL;//结束创建
return head;
}
修改链表节点值
修改链表节点值很简单。下面是一个传入链表和要修改的节点,来修改值的函数。
void change(LinkList *list,int n) {//n为第n个节点
LinkList *t = list;
int i = 0;
while (i < n && t != NULL) {
t = t->next;
i++;
}
if (t != NULL) {
puts("输入要修改的值");
scanf("%d", &t->score);
}
else {
puts("节点不存在");
}
}
删除链表节点
删除链表的元素也就是把前节点的指针域越过要删除的节点指向下下个节点。即:p->next = q->next;然后放出q节点的空间,即free(q);
void delet(LinkList *list, int n) {
LinkList *t = list, *in;
int i = 0;
while (i < n && t != NULL) {
in = t;
t = t->next;
i++;
}
if (t != NULL) {
in->next = t->next;
free(t);
}
else {
puts("节点不存在");
}
}
插入链表节点
我们可以看出来,插入节点就是用插入前节点的指针域链接上插入节点的数据域,再把插入节点的指针域链接上插入后节点的数据域。根据图,插入节点也就是:e->next = head->next; head->next = e;
增加链表节点用到了两个结构体指针和一个int数据。
void insert(LinkList *list, int n) {
LinkList *t = list, *in;
int i = 0;
while (i < n && t != NULL) {
t = t->next;
i++;
}
if (t != NULL) {
in = (LinkList*)malloc(sizeof(LinkList));
puts("输入要插入的值");
scanf("%d", &in->score);
in->next = t->next;//填充in节点的指针域,也就是说把in的指针域指向t的下一个节点
t->next = in;//填充t节点的指针域,把t的指针域重新指向in
}
else {
puts("节点不存在");
}
}
输出链表
输出链表很简单,边遍历边输出就行了。
while (h->next != NULL) {
h = h->next;
printf("%d ", h->score);
栈
栈是一种操作受限的线性表只允许从一端插入和删除数据。栈有两种存储方式,即线性存储和链接存储(链表)。栈的一个最重要的特征就是栈的插入和删除只能在栈顶进行,所以每次删除的元素都是最后进栈的元素,故栈也被称为后进先出(LIFO)表。每个栈都有一个栈顶指针,它初始值为-1,且总是指向最后一个入栈的元素,栈有两种处理方式,即进栈(push)和出栈(pop),因为在进栈只需要移动一个变量存储空间,所以它的时间复杂度为O(1),但是对于出栈分两种情况,栈未满时,时间复杂度也为O(1),但是当栈满时,需要重新分配内存,并移动栈内所有数据,所以此时的时间复杂度为O(n)。以下举例栈结构的两种实现方式,线性存储和链接存储。
1、线性存储
线性存储的方式和线性表基本一致,只不过多了后进先出的限制而已,它是静态分配的,即使用前,它的内存就已经以数组的形式分配好了,所以在初始化时,需要指明栈的节点最大个数。
#include "stdafx.h"
#include <iostream>
#include <new>
//定义
template<class T>
class LineStack
{
public :
LineStack(int MaxListSize=10); //构造函数
~LineStack() //析构函数
{
delete[] elements;
}
bool IsEmpty() const //判断是否为空
{
return top==-1;
}
bool IsFull() const //判断是否满
{
return top==MaxSize-1;
}
T pop(); //出栈
int push(const T& data); //进栈
T getPop(); //获取栈顶元素值
void clear(); //清空栈
void print() ;
private:
int top; //栈顶指针
int MaxSize; //数组最大长度
T *elements;//一维动态数组
};
//实现...
template<class T>
LineStack<T>::LineStack(int MaxListSize)
{
//基于公式的线性表的构造函数
MaxSize = MaxListSize;
elements = new T[MaxSize];
top = -1;
}
template<class T>
T LineStack<T>::pop()
{
if(IsEmpty())
{
return NULL;
}
return elements[top--];
}
template<class T>
int LineStack<T>::push(const T& data)
{
if(IsFull())
{
return -1;
}
else
{
elements[++top] = data;
}
return 0;
}
template<class T>
T LineStack<T>::getPop()
{
if(IsEmpty())
{
return NULL;
}
return elements[top];
}
template<class T>
void LineStack<T>::clear()
{
top = -1;
return true;
}
template<class T>
void LineStack<T>::print()
{
for(int i=0;i<=top;i++)
{
std:: cout<<elements[i]<<" ";
}
}
void LineStackSample()
{
int j;
int a = 10,b = 20,c = 30,d = 40;
LineStack<int> S(10);
std::cout<<"IsFull = "<<S.IsFull()<<std::endl;
std::cout<<"IsEmpty = "<<S.IsEmpty()<<std::endl;
S.push(a);
S.push(b);
S.push(c);
S.push(d);
j = S.pop();
std::cout<<j<<std::endl;
j = S.pop();
std::cout<<j<<std::endl;
j = S.pop();
std::cout<<j<<std::endl;
j = S.pop();
std::cout<<j<<std::endl;
return;
}
int main(int argc, _TCHAR* argv[])
{
LineStackSample();
//暂停操作
char str;
std::cin>>str;
//程序结束
return 0;
}
2、链接存储
实际上只要对单链表类做适当的修改,限制其插入、删除、修改和访问结点的行为,使其符合栈先进后出的规则即可,另外需要单独提供栈访问的接口函数,例如进栈、出栈、获取栈大小等,链表知识可以参考https://blog.csdn.net/Chiang2018/article/details/82730174。
// 栈动态.cpp : 定义控制台应用程序的入口点。
//
// 单链表.cpp : 定义控制台应用程序的入口点。
//
#include "stdafx.h"
#include <stdlib.h>
#include <iostream>
template <class T>
class Node
{
public:
T data;
Node(T& item);
Node<T>* next;
};
template<class T>
class LinkList
{
public:
LinkList();
~LinkList();
int getSize(void);
bool IsEmpty(void);
int gotoNext(void);
int getPostion(void);
int InsertNode(T& data);
int DeleteNode(void);
void getCurrNodeData(T& data);
void setCurrNodeData(T& data);
void clear();
void print();
private:
Node<T>* head;
Node<T>* currNode;
int size;
int position;
void freeNode(Node<T>* p);
};
/* 链表节点构造函数 */
template <class T>
Node<T>::Node(T& item)
{
data = item;
next = NULL;
}
/* 链表构造函数 */
template <class T>
LinkList<T>::LinkList()
{
head = NULL;
currNode = NULL;
size = 0;
position = -1;
}
/* 链表析构函数 */
template <class T>
LinkList<T>::~LinkList()
{
clear();
}
/* 获取链表长度 */
template <class T>
int LinkList<T>::getSize(void)
{
return size;
}
/* 判断链表是否为空 */
template <class T>
bool LinkList<T>::IsEmpty(void)
{
return size==0?true:false;
}
/* 移动到下个节点,返回下个节点的位置值 */
template <class T>
int LinkList<T>::gotoNext(void)
{
if(NULL == head)
{
return -1;
}
if(NULL == currNode)
{
return -1;
}
else
{
currNode = currNode->next;
position++
}
return position;
}
/* 获取当前节点的位置 */
template <class T>
int LinkList<T>::getPostion(void)
{
return position;
}
/* 在当前节点前插入新节点 */
template <class T>
int LinkList<T>::InsertNode(T& data)
{
Node<T>* p = new Node<T>(data);
if(0 == size)
{
head = p;
head->next = NULL;
currNode = p;
}
else
{
p->next = currNode->next;
currNode->next = p;
currNode = p;
}
size++;
position++;
return size;
}
/* 删除当前节点 */
template <class T>
int LinkList<T>::DeleteNode(void)
{
if(0 == size)
{
return -1;
}
Node<T>* p = head;
Node<T>* tmp;
for(int i = 0;i < size;i++)
{
if(NULL == p)
{
return -1;
}
if(p->next == currNode)
{
p->next = currNode->next;
break;
}
p = p->next;
}
tmp = currNode;
if(currNode == head)
{
head = currNode->next;
}
if(NULL == currNode->next)
{
position--;
currNode = p;
}
else
{
currNode = currNode->next;
}
freeNode(p);
size--;
if(0 == size)
{
position = -1;
}
return 0;
}
/* 释放指定节点的内存 */
template <class T>
void LinkList<T>::freeNode(Node<T>* p)
{
if(!p)
{
delete p;
}
return;
}
/* 获取当前节点的数据 */
template <class T>
void LinkList<T>::getCurrNodeData(T& data)
{
if(currNode)
{
data = currNode->data;
}
return ;
}
/* 修改当前节点的数据 */
template <class T>
void LinkList<T>::setCurrNodeData(T& data)
{
if(currNode)
{
currNode->data = data;
}
return ;
}
/* 清空链表 */
template <class T>
void LinkList<T>::clear()
{
if(0 == size)
{
return;
}
Node<T>* p = head;
Node<T>* tmp = head->next;
while(p)
{
freeNode(p);
p = tmp;
if(tmp)
{
tmp = tmp->next;
}
}
head = NULL;
currNode = NULL;
size = 0;
position = -1;
return;
}
template <class T>
void LinkList<T>::print()
{
if(0 == size)
{
return;
}
Node<T>* p = head;
Node<T>* tmp = head->next;
while(p)
{
std::cout<<p->data<<std::endl;
p = tmp;
if(tmp)
{
tmp = tmp->next;
}
}
return;
}
template <class T>
class LinkedStack
{
private:
LinkList<T>* link;
public:
LinkedStack();
void push(T& data);
T pop();
void ClearStack();
int getSize();
bool isEmpty();
};
template <class T>
LinkedStack<T>::LinkedStack()
{
link = new LinkList<T>;
}
template <class T>
bool LinkedStack<T>::isEmpty()
{
return link->IsEmpty();
}
template <class T>
int LinkedStack<T>::getSize()
{
return link->size;
}
template <class T>
void LinkedStack<T>::ClearStack()
{
link->clear();
}
template <class T>
void LinkedStack<T>::push(T& data)
{
link->InsertNode(data);
}
template <class T>
T LinkedStack<T>::pop()
{
T tmp;
if(isEmpty())
{
return NULL;
}
link->getCurrNodeData(tmp);
link->DeleteNode();
return tmp;
}
int main(int argc, _TCHAR* argv[])
{
int j = 0;
int a = 10,b=20,c=30,d=40,e=50;
LinkedStack<int> list;
list.push(a);
list.push(b);
list.push(c);
list.push(d);
list.push(e);
j = list.pop();
std::cout<<j<<std::endl;
j = list.pop();
std::cout<<j<<std::endl;
j = list.pop();
std::cout<<j<<std::endl;
j = list.pop();
std::cout<<j<<std::endl;
j = list.pop();
std::cout<<j<<std::endl;
std::cin.get();
return 0;
}
队列
队列是一种先进先出的数据类型
队列通常可以分为两种类型:
一、顺序队列,采用顺序存储,当长度确定时使用。 顺序队列又有两种情况:
①使用数组存储队列的称为静态顺序队列。
②使用动态分配的指针的称为动态顺序队列。
二、链式队列,采用链式存储,长度不确定时使用(由链表实现)。
由于链式队列跟链表差不多,所以在这里只针对循环(环形)队列来说明并实践。
循环队列的两个参数:
①front,front指向队列的第一个元素。(front==head)
②rear,rear指向队列的最后一个有效元素的下一元素。(rear==tail)
队列的两个基本操作:出队和入队。
入队(尾部入队)
①将值存入rear所代表的位置。
②rear = (rear+1)%数组的长度。
出队(头部出队)
front = (front+1)%数组的长度。
队列是否为空
front和rear的值相等,则该队列就一定为空。
队列是否已满
在循环队列中,“队满”和“队空”的条件有可能是相同的,都是front ==rear,这种情况下,无法区别是“队满”还是“队空”。
针对这个问题,有3种可能的处理方法: 【这里采用了第3种处理方法】
(1)另设一个标志以区别是“队满”还是“队空”。(即入队/出队前检查是否“队满”/“队空”)
(2)设一个计数器,此时甚至还可以省去一个指针。
(3)少用一个元素空间,即约定队头指针在队尾指针的下一位置时就作为“队满”的标志,即“队满”条件为:(pQueue->rear+1)%MAX_SIZE == pQueue->front。
随着入队、出队的进行,会使整个队列整体向后移动,就会出现上图中的现象:队尾指针已经移到了最后,即队尾出现溢出,无法再进行入队操作,然而实际上,此时队列中还有空闲空间,这种现象称为“假溢出”。
解决“假溢出”的三种办法:
- 方法一:每次删除队头元素后,把整个队列向前移动一个位置,这样可保证队头元素在存储空间的最前面。但每次删除元素时,都要把表中所有元素向前移动,效率太低。
- 方法二:当队尾指针出现溢出时,判断队头指针位置,如果前部有空闲空间,则把当前队列整体前移到最前方。这种方法移动元素的次数大为减少。
- 方法三:将队列看成头尾相接的循环结构,当队尾指针到队尾后,再从队头开始向后指,这样就不需要移动队列元素了,显然,第三种方法最经济、应用最多,这种顺序队列被称为“循环队列”或“环形队列”。
采用了这种头尾相接的循环队列后,入队的队尾指针加1操作及出队的队头指针加1操作必须做相应的修改,以确保下标范围为0~Max_Size-1。对指针进行取模运算,就能使指针到达最大下标位置后回到0,符合“循环”队列的特点。
因此入队时队尾指针加1操作改为: pQueue->tail = (pQueue->tail+1) % MAX_SIZE;
入队时队尾指针加1操作改为: pQueue->head = (pQueue->head+1) % MAX_SIZE;
顺序队列
//
// main.c
// SequenceQueue
//
// Created by Eason on 2020/8/2.
// Copyright © 2020 Eason. All rights reserved.
//
#include <stdio.h>
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXSIZE 21 //采用循环队列的方式,充分利用空间,但是会有一个单元的浪费,实际容量为最大容量-1,因为要区分空与满
typedef int ElemType;
typedef int Status;
typedef struct{ //顺序队列的存储结构
ElemType data[MAXSIZE]; //队列元素的数据
int front, rear; //头指针与尾指针
}SqQueue;
//初始化顺序队列
Status initQueue(SqQueue *Q){
Q->front=0; //初始时头指针与为指针均指向0
Q->rear=0;
return OK;
}
//判断顺序队列是否为空
Status isEmpty(SqQueue Q){
if(Q.front==Q.rear){ //当头指针与尾指针指向相同的单元时表示队列为空
return TRUE;
}else{
return FALSE;
}
}
//判断顺序队列是否已满
Status isFull(SqQueue Q){
if((Q.rear+1)%MAXSIZE==Q.front){ //循环队列头指针可能在前也可能在后,头指针在前尾指针在最后差1时为满,头指针在后尾指针与头指针差1时为满,则用差值取余的方式可判断当前是否已满
return TRUE;
}else{
return FALSE;
}
}
//获取顺序队列的长度
Status getLength(SqQueue Q){
return (Q.rear-Q.front+MAXSIZE)%MAXSIZE; //根据循环队列的特点,即长度为差值加最大容量与最大容量的取模运算
}
//清空顺序队列
Status clearQueue(SqQueue *Q){
Q->front = Q->rear; //根据队列为空的判断条件,即将头指针指向尾指针时两指针指向同一单元时队列为空。不能颠倒,因为尾指针指向的是空单元
return OK;
}
//入队
Status enter(SqQueue *Q, ElemType *e){
if(isFull(*Q)){ //判断队列是否还可以再入队元素
printf("队列已满,无法入队\n");
return ERROR;
}
Q->data[Q->rear]=e; //将当前尾指针指向的空白单元入值
Q->rear = (Q->rear+1)%MAXSIZE; //将尾指针向后走一格,因为有可能是从队尾到队头,所以使用取模的方式判断尾指针接下来的位置
return OK;
}
//出队
Status leave(SqQueue *Q, ElemType *e){
if(isEmpty(*Q)){ //判断队列是否有元素可以出队
printf("队列为空,不可出队\n");
return ERROR;
}
*e = Q->data[Q->front]; //将当前队首元素出队给e供返回与查看
Q->front = (Q->front+1)%MAXSIZE; //将头指针向后走一格,因为有可能是从队尾到队头,所以使用取模的方式判断头指针接下来的位置
return OK;
}
//获取队首元素
Status getHead(SqQueue Q, ElemType *e){
if(isEmpty(Q)){ //判断队列是否有元素可供查看
printf("队列为空,无队首元素\n");
return ERROR;
}
*e = Q.data[Q.front]; //将当前队头元素返回给e供返回并查看
return OK;
}
//打印队列
Status printQueue(SqQueue Q){
if(isEmpty(Q)){ //判断队列当前是否有元素可供打印
printf("队列为空,无队元素可供打印\n");
return ERROR;
}
int i=0; //当前元素数量计数器
while(!isEmpty(Q)){
i++; //不为空说明当前有元素可供打印,则计数器+1
printf("从队首至队尾的第%d个元素为:%d\n", i, Q.data[Q.front]); //打印当前队首元素
Q.front = (Q.front+1)%MAXSIZE; //将头指针向后走一格,因为有可能是从队尾到队头,所以使用取模的方式判断头指针接下来的位置
}
return OK;
}
//测试
int main(int argc, const char * argv[]) {
SqQueue Q;
initQueue(&Q);
printf("初始化队列Q后队列的长度为:%d,是否为空?(是1否0):%d\n", getLength(Q), isEmpty(Q));
printf("将1-18顺序的入队后队列变为:\n");
for(int i=1;i<=18;i++){
enter(&Q, i);
}
printQueue(Q);
printf("此时队列的长度为:%d\n", getLength(Q));
printf("队列的最大长度为20,检验再依次入队3个元素后得:\n");
enter(&Q, 19);
enter(&Q, 20);
enter(&Q, 21);
printQueue(Q);
printf("-----验证循环队列-----\n");
int e;
leave(&Q, &e);
printf("出队列:%d\n", e);
enter(&Q, 21);
printf("入队列:21\n");
printf("此时的队列内容为:\n");
printQueue(Q);
printf("此时队列的长度为:%d,是否已满?(1是0否):%d\n", getLength(Q), isFull(Q));
printf("清空队列后队列为:\n");
clearQueue(&Q);
printQueue(Q);
return 0;
}
链队列
//
// main.c
// LinkedQueue
//
// Created by Eason on 2020/8/2.
// Copyright © 2020 Eason. All rights reserved.
//
#include <stdio.h>
#include <stdlib.h>
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
typedef int ElemType;
typedef int Status; //注意:头指针始终指向头结点(不存放数据)头结点的下一结点才是链队的队头
typedef struct QueueNode{ //链队结点的存储结构
ElemType data; //数据域
struct QueueNode *next; //指针域
}QueueNode, *QueueNodePtr;
typedef struct{ //链队头结点的存储结构
QueueNodePtr front, rear; //头指针与尾指针
}LinkQueue;
//初始化链队
Status initQueue(LinkQueue *Q){
Q->front = (QueueNodePtr)malloc(sizeof(QueueNode)); //初始化为首位指针分配内存
Q->rear = (QueueNodePtr)malloc(sizeof(QueueNode));
if(!Q->front || !Q->rear){ //若不存在则说明内存分配失败无法初始化
printf("初始化内存分配失败");
return ERROR;
}
Q->front = Q->rear; //空队的条件 队头指针=队尾指针 均指向头结点
Q->front->next = NULL; //头结点的下一结点,即首个结点为空
return OK; //这里要注意,初始的时候首位指针均指向头结点,是不存放数据的,链队此时为空
}
//判断链队是否为空
Status isEmpty(LinkQueue Q){
if(Q.front==Q.rear){ //链队为空的条件为头指针=尾指针,即都指向头结点
return TRUE;
}else{
return FALSE;
}
}
//获取链队的长度
int getLength(LinkQueue Q){
QueueNodePtr p; //定义临时结点指针
p = Q.front->next; //将临时结点置为链队的首个结点
int i=0; //链队长度计数器
while(p){ //如果此时链队结点存在的话就继续向下进行
i++; //计数器+1
p = p->next; //链队指针继续向下移动
}
return i; //返回链队计数器i即长度
}
//入队
Status enter(LinkQueue *Q, ElemType *e){
QueueNodePtr p = (QueueNodePtr)malloc(sizeof(QueueNode)); //为新入队的结点分配内存空间
if(!p){ //验证是否为新结点内存分配成功
printf("新结点内存分配失败,无法入队");
return ERROR;
}
p->data = e; //将新结点的数据域置为指定值
Q->rear->next = p; //还未入队的此时队尾的下一结点指向p
Q->rear = p; //这时队尾指针指向p,即p成为了新的队尾结点
p->next = NULL; //队尾结点的指针域为空
return OK;
}
//出队
Status leave(LinkQueue *Q, ElemType *e){
if(isEmpty(*Q)){ //判断链队是否为空,若为空则无链队元素可供出队
printf("链队为空,无队元素可出列\n");
return ERROR;
}
QueueNodePtr p; //定义临时结点指针p
p = Q->front->next; //将p置为链队的首个结点
*e = p->data; //将首个结点p的数据域赋给e以供返回与查看
Q->front->next = p->next; //将老首个结点的下一结点设置为首个结点
if(Q->rear == p){ //若此时p也为尾结点,说明队列为空了
Q->rear = Q->front; //如果队列为空则将队尾指针重新指向头结点表示链队为空了
}
free(p); //将出队的p结点释放掉
return OK;
}
//获取链队的队头元素
Status getHead(LinkQueue Q, ElemType *e){
if(isEmpty(Q)){ //判断链队是否为空,若为空则无链队的队头元素可供查看
printf("链队为空,无队头元素\n");
return ERROR;
}
*e = Q.front->next->data; //若链队不为空,则将链队的首个结点的数据域赋给e供返回与查看
return OK; //仅查看队头元素,指针不发生移动
}
//清空链队
Status clearQueue(LinkQueue *Q){
QueueNodePtr p, q; //定义临时结点pq
p = Q->front->next; //将p结点置为链队的首个结点
Q->rear = Q->front; //将队尾指针指向头结点与头指针相同,这样则表示此时链队为空
Q->front->next = NULL; //将头结点的指针域置空,即无首个结点
while(p){ //若p存在则继续执行循环体
q = p; //将p赋给q
p = p->next; //p继续向下进行
free(q); //释放q,一直循环直到p结点不再存在,即此时链队的结点都被释放掉了
}
return OK;
}
//打印链队
Status printQueue(LinkQueue Q){
if(isEmpty(Q)){ //判断链队是否为空,若为空则无链队元素可供打印
printf("当前链队无元素可供打印\n");
return ERROR;
}
QueueNodePtr p; //定义临时结点p
p = Q.front->next; //将p赋为链队的首个结点
int i=0; //此时链队元素位置计数器
while(p){ //如果此时p存在的话则继续执行循环体
i++; //p存在则计数器+1
printf("从队首至队尾的第%d个元素为:%d\n", i, p->data); //打印当前p结点的数据域
p = p->next; //p指针继续向下移动,直到p为空,即链队的所有结点都打印完毕
}
return OK;
}
//测试
int main(int argc, const char * argv[]) {
LinkQueue Q;
initQueue(&Q);
printf("初始化队列Q后队列的长度为:%d\n此时的链队是否为空?(1是0否):%d\n", getLength(Q), isEmpty(Q));
printf("将1-6按顺序入队后可得链队:\n");
for(int i=1;i<=6;i++){
enter(&Q, i);
}
printQueue(Q);
printf("此时队列的长度为:%d\n", getLength(Q));
int e;
getHead(Q, &e);
printf("此时队列的队头为:%d\n", e);
printf("队列出队两个元素:\n");
leave(&Q, &e);
printf("出队:%d\n", e);
leave(&Q, &e);
printf("出队:%d\n", e);
printf("现在的链队为:\n");
printQueue(Q);
printf("现在的链队长度为:%d\n", getLength(Q));
getHead(Q, &e);
printf("现在链队的队头为:%d\n", e);
printf("清空链队后得链队为:\n");
clearQueue(&Q);
printQueue(Q);
return 0;
}
数组和广义表
1、数组
数组的特点:
元素数目固定;下标有界。
数组的操作:
按照下标进行读写。
2、数组的顺序表示和实现
因计算机的内存结构是一维的,因此用一维内存来表示多维数组,就必须按某种次序将数组元素排成一列序列,然后将这个线性序列存放在储存器中。
通常有两种顺序存储方式:
(1)行优先顺序——将数组元素按行排列
在PASCAL、C语言中,数组就是按行优先顺序储存。
(2)列优先顺序——将数组按列向量排列。
在FORTRAN语言中,数组就是按列优先顺序储存的。
3、矩阵的压缩储存
利用2维数组描述矩阵
特殊矩阵:
为了节省储存空间,矩阵进行压缩存储:即为多个相同的非零的元素值分配一个储存空间;对0元素不分配空间。
(1)对称矩阵
只需对对称矩阵中n(n+1)/2个元素进行储存表示
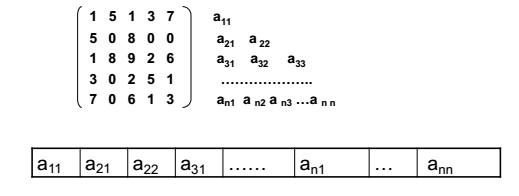

(2)三角矩阵


(3)稀疏矩阵
if 一个m*n的矩阵含有t个非零元素,且t远远小于m*n,则称这个矩阵为稀疏矩阵

利用三元组表示法对稀疏矩阵进行压缩储存
用三项内容表示稀疏矩阵中的每个非零元素,进行形式为:(i,j,value)
其中,i 表示行序号,j 表示列序号,value 表示非零元素的值

| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
|
稀疏矩阵的转置
转置前矩阵为M,转置后为T,M的列为T的行,因此,要按M.data的列序转置
所得到的转置矩阵T的三元组表必定按行优先存放
转置算法:
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
|
这个转置算法的时间复杂度为O(n*t),效率太低了
快速转置算法
一遍扫描先确定三元组的位置关系,二次扫描由位置关系装入三元组
为了预先确定矩阵M中的每一列的第一个非零元素在数组B中应有的位置,需要闲球的矩阵M中的每一列中非零元素的个数。
为此,需要设计两个一位数组num[0...n-1]和cpot[1..n-1]
num[0...n-1]:统计M中每一列非零元素的个数
cpot[0...n-1]:由递推关系得出M中的每列第一个非零元素在B中的位置
cpot[col]=cpot[col-1]+num[col-1];
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
|
时间复杂度为O(n+t)
4、广义表的定义



第 6 章 树和二叉树
0X01 树的概念
1. 树的定义
树是一种数据结构,它是由n(n>=1)个有限节点组成一个具有层次关系的集合。
把它叫做“树”是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。它具有以下的特点:
(01) 每个节点有零个或多个子节点;
(02) 没有父节点的节点称为根节点;
(03) 每一个非根节点有且只有一个父节点;
(04) 除了根节点外,每个子节点可以分为多个不相交的子树。
2. 树的基本术语
若一个结点有子树,那么该结点称为子树根的"双亲",子树的根是该结点的"孩子"。有相同双亲的结点互为"兄弟"。一个结点的所有子树上的任何结点都是该结点的后裔。从根结点到某个结点的路径上的所有结点都是该结点的祖先。
结点的度:结点拥有的子树的数目。
叶子:度为零的结点。
分支结点:度不为零的结点。
树的度:树中结点的最大的度。
层次:根结点的层次为1,其余结点的层次等于该结点的双亲结点的层次加1。
树的高度:树中结点的最大层次。
无序树:如果树中结点的各子树之间的次序是不重要的,可以交换位置。
有序树:如果树中结点的各子树之间的次序是重要的, 不可以交换位置。
森林:0个或多个不相交的树组成。对森林加上一个根,森林即成为树;删去根,树即成为森林。
0X02 二叉树的介绍
1. 二叉树的定义
二叉树是每个节点最多有两个子树的树结构。它有五种基本形态:二叉树可以是空集;根可以有空的左子树或右子树;或者左、右子树皆为空。
2. 二叉树的性质
二叉树有以下几个性质:TODO(上标和下标)
性质1:二叉树第i层上的结点数目最多为 2{i-1} (i≥1)。
性质2:深度为k的二叉树至多有2{k}-1个结点(k≥1)。
性质3:包含n个结点的二叉树的高度至少为log2 (n+1)。
性质4:在任意一棵二叉树中,若终端结点的个数为n0,度为2的结点数为n2,则n0=n2+1。
2.1 性质1:二叉树第i层上的结点数目最多为 2{i-1} (i≥1)
证明:下面用"数学归纳法"进行证明。
(01) 当i=1时,第i层的节点数目为2{i-1}=2{0}=1。因为第1层上只有一个根结点,所以命题成立。
(02) 假设当i>1,第i层的节点数目为2{i-1}。这个是根据(01)推断出来的!
下面根据这个假设,推断出"第(i+1)层的节点数目为2{i}“即可。
由于二叉树的每个结点至多有两个孩子,故"第(i+1)层上的结点数目” 最多是 “第i层的结点数目的2倍”。即,第(i+1)层上的结点数目最大值=2×2{i-1}=2{i}。
故假设成立,原命题得证!
2.2 性质2:深度为k的二叉树至多有2{k}-1个结点(k≥1)
证明:在具有相同深度的二叉树中,当每一层都含有最大结点数时,其树中结点数最多。利用"性质1"可知,深度为k的二叉树的结点数至多为:
20+21+…+2k-1=2k-1
故原命题得证!
2.3 性质3:包含n个结点的二叉树的高度至少为log2 (n+1)
证明:根据"性质2"可知,高度为h的二叉树最多有2{h}–1个结点。反之,对于包含n个节点的二叉树的高度至少为log2(n+1)。
2.4 性质4:在任意一棵二叉树中,若终端结点的个数为n0,度为2的结点数为n2,则n0=n2+1
证明:因为二叉树中所有结点的度数均不大于2,所以结点总数(记为n)=“0度结点数(n0)” + “1度结点数(n1)” + “2度结点数(n2)”。由此,得到等式一。
(等式一) n=n0+n1+n2
另一方面,0度结点没有孩子,1度结点有一个孩子,2度结点有两个孩子,故二叉树中孩子结点总数是:n1+2n2。此外,只有根不是任何结点的孩子。故二叉树中的结点总数又可表示为等式二。
(等式二) n=n1+2n2+1
由(等式一)和(等式二)计算得到:n0=n2+1。原命题得证!
3. 满二叉树,完全二叉树和二叉查找树
3.1 满二叉树
定义:高度为h,并且由2{h} –1个结点的二叉树,被称为满二叉树。
3.2 完全二叉树
定义:一棵二叉树中,只有最下面两层结点的度可以小于2,并且最下一层的叶结点集中在靠左的若干位置上。这样的二叉树称为完全二叉树。
特点:叶子结点只能出现在最下层和次下层,且最下层的叶子结点集中在树的左部。显然,一棵满二叉树必定是一棵完全二叉树,而完全二叉树未必是满二叉树。
3.3 二叉查找树
定义:二叉查找树(Binary Search Tree),又被称为二叉搜索树。设x为二叉查找树中的一个结点,x节点包含关键字key,节点x的key值记为key[x]。如果y是x的左子树中的一个结点,则key[y] <= key[x];如果y是x的右子树的一个结点,则key[y] >= key[x]。
另一种定义:根节点的值大于等于其左子树中任意一个节点的值,小于等于其右节点中任意一节点的值,这一规则适用于二叉查找树中的每一个节点。
在二叉查找树中:
(01) 若任意节点的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
(02) 任意节点的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
(03) 任意节点的左、右子树也分别为二叉查找树。
(04) 没有键值相等的节点(no duplicate nodes)。
在实际应用中,二叉查找树的使用比较多。
结点的度:一个结点的子树数目称为该结点的度。(例如结点1的结点的度为3,结点2的结点的度为3,结点3的结点的度为0)。
树的度:所有结点度当中,度最高的一个。(上图树的度是3)。
叶子结点:上图应该是:3、5、6、7、9、10
分之结点:除了叶子结点,其他的都称为分之结点,和叶子结点构成互补的关系。(1、2、4、8)
内部结点:分之结点除了根结点以外的。(2、4、8)
父结点:如5号结点就是2号结点的子结点。
子结点:2号结点是5号结点的父结点。
兄弟结点:5、6、7称为兄弟结点,出自同一个父亲2号结点。
这三个概念是一个相对的概念。
层次:0层、1层、2层、3层。
还有一个公式就能做题了:总结点=所有度结点的和+1(应该是父结点)
树的遍历:
前序遍历:先从根部出发,然后由左向右,一颗一颗树来完成遍历。先访问根再访问叶子结点,这就是我画出来的前序遍历图,箭头的方向表示遍历的顺序。
后序遍历:顾名思义,就是从叶子结点出发,先遍历叶子结点再到根结点,最后到父结点。
层次遍历:按0层、1层、2层、3层,从左到右来遍历
我们接着就可以来理解二叉树的重要的特性:
我们找五颗二叉树来进行分析:这样分析就简单多了,我都觉得不用分析了,但是还是说说吧。
1、二叉树中,第i层上最多有2的i次方个结点(i>=0)。这个很基本,这也是二叉树和树的区别。
2、深度为K的二叉树至多有2的(k+1)次方 -1个结点(k>=0)。(深度为二叉树中层数最大的叶节点的层数),满二叉树的深度为2,则共有7个结点。
3、对任何一颗二叉树,如果其叶子结点数为n0,度为2的结点数为n2,则n0=n2+1;(一定不要忘了根结点的度也是2)。
二叉树核心代码
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
typedef char dataype_bt; //声明二叉树中存放的数据类型,便于后续更改
typedef struct btreenode{ //二叉树的节点结构:存放的数据 该节点的左子节点地址及右子节点地址。注意和单链表的区别,二叉树是非线性存储,单链表是线性存储
dataype_bt data;
struct btreenode *lchild,*rchild;
}btree_node,*btree_pnode;
extern btree_pnode create_btree1(void); //通过递归方法创建一个二叉树
extern void create_btree(btree_pnode *T); //通过递归方法创建一个二叉树(功能同上)
extern void pre_order(btree_pnode t); //采用递归方法先序遍历
extern void unpre_order(btree_pnode t); //采用非递归方法先序遍历
extern void mid_order(btree_pnode t); //采用递归方法中序遍历
extern void post_order(btree_pnode t); //采用递归方法后序遍历
extern void level_order(btree_pnode t); //层次遍历
extern void travel(char const *str,void (*pfun)(btree_pnode),btree_pnode t); //将上面的函数作为参数传入该函数(函数的回调),实现二叉树的创建 和 遍历,其中参数str可以是回调函数的功能描述
#endif线索二叉树原理
遍历二叉树的其实就是以一定规则将二叉树中的结点排列成一个线性序列,得到二叉树中结点的先序序列、中序序列或后序序列。这些线性序列中的每一个元素都有且仅有一个前驱结点和后继结点。
但是当我们希望得到二叉树中某一个结点的前驱或者后继结点时,普通的二叉树是无法直接得到的,只能通过遍历一次二叉树得到。每当涉及到求解前驱或者后继就需要将二叉树遍历一次,非常不方便。
于是是否能够改变原有的结构,将结点的前驱和后继的信息存储进来。
二叉树结构
观察二叉树的结构,我们发现指针域并没有充分的利用,有很多“NULL”,也就是存在很多空指针。
对于一个有n个结点的二叉链表,每个节点都有指向左右孩子的两个指针域,一共有2n个指针域。而n个结点的二叉树又有n-1条分支线数(除了头结点,每一条分支都指向一个结点),也就是存在2n-(n-1)=n+1个空指针域。这些指针域只是白白的浪费空间。因此, 可以用空链域来存放结点的前驱和后继。线索二叉树就是利用n+1个空链域来存放结点的前驱和后继结点的信息。
线索二叉树
如图以中序二叉树为例,我们可以把这颗二叉树中所有空指针域的lchild,改为指向当前结点的前驱(灰色箭头),把空指针域中的rchild,改为指向结点的后继(绿色箭头)。我们把指向前驱和后继的指针叫做线索 ,加上线索的二叉树就称之为线索二叉树。
线索二叉树结点结构
如果只是在原二叉树的基础上利用空结点,那么就存在着这么一个问题:我们如何知道某一结点的lchild是指向他的左孩子还是指向前驱结点?rchild是指向右孩子还是后继结点?显然我们要对他的指向增设标志来加以区分。
因此,我们在每一个结点都增设两个标志域LTag和RTag,它们只存放0或1的布尔型变量,占用的空间很小。于是结点的结构如图所示。
结点结构
其中:
LTag为0是指向该结点的左孩子,为1时指向该结点的前驱
RTag为0是指向该结点的右孩子,为1时指向该结点的后继
因此实际的二叉链表图为
实际的二叉链表图
线索二叉树的结构实现
二叉树的线索存储结构定义如下:
typedef char TElemType;
typedef enum { Link, Thread } PointerTag; //Link==0,表示指向左右孩子指针
//Thread==1,表示指向前驱或后继的线索
//二叉树线索结点存储结构
typedef struct BiThrNode {
TElemType data; //结点数据
struct BiThrNode *lchild, *rchild; //左右孩子指针
PointerTag LTag;
PointerTag RTag; //左右标志
}BiThrNode, *BiThrTree;
二叉树线索化
线索化
对普通二叉树以某种次序遍历使其成为线索二叉树的过程就叫做线索化。因为前驱和后继结点只有在二叉树的遍历过程中才能得到,所以线索化的具体过程就是在二叉树的遍历中修改空指针。
线索化具体实现
以中序二叉树的线索化为例,线索化的具体实现就是将中序二叉树的遍历进行修改,把原本打印函数的代码改为指针修改的代码就可以了。
我们设置一个pre指针,永远指向遍历当前结点的前一个结点。若遍历的当前结点左指针域为空,也就是无左孩子,则把左孩子的指针指向pre(相对当前结点的前驱结点)。
右孩子同样的,当pre的右孩子为空,则把pre右孩子的指针指向当前结点(相对pre结点为后继结点)。
最后把当前结点赋给pre,完成后续的递归遍历线索化。
中序遍历线索化的递归函数代码如下:
void InThreading(BiThrTree B,BiThrTree *pre) {
if(!B) return;
InThreading(B->lchild,pre);
//--------------------中间为修改空指针代码---------------------
if(!B->lchild){ //没有左孩子
B->LTag = Thread; //修改标志域为前驱线索
B->lchild = *pre; //左孩子指向前驱结点
}
if(!(*pre)->rchild){ //没有右孩子
(*pre)->RTag = Thread; //修改标志域为后继线索
(*pre)->rchild = B; //前驱右孩子指向当前结点
}
*pre = B; //保持pre指向p的前驱
//---------------------------------------------------------
InThreading(B->rchild,pre);
}
增设头结点
线索化后的二叉树,就如同操作一个双向链表。于是我们想到为二叉树增设一个头结点,这样就和双向链表一样,即能够从第一个结点正向开始遍历,也可以从最后一个结点逆向遍历。
增设头结点
如上图,在线索二叉链表上添加一个head结点,并令其lchild域的指针指向二叉树的根结点(A),其rchild域的指针指向中序遍历访问的最后一个结点(G)。同样地,二叉树中序序列的第一个结点中,lchild域指针指向头结点,中序序列的最后一个结点rchild域指针也指向头结点。
于是从头结点开始,我们既可以从第一个结点顺后继结点遍历,也可以从最后一个结点起顺前驱遍历。就和双链表一样。
双链表
增设头结点并线索化的代码实现
//为线索二叉树添加头结点,使之可以双向操作
Status InOrderThreading(BiThrTree *Thrt,BiThrTree T){
if(!(*Thrt = (BiThrTree)malloc(sizeof(BiThrNode)))) exit(OVERFLOW); //开辟结点
(*Thrt)->LTag = Link;
(*Thrt)->RTag = Thread; //设置标志域
(*Thrt)->rchild = (*Thrt); //右结点指向本身
if(!T) {
(*Thrt)->lchild = (*Thrt);
return OK; //若根结点不存在,则该二叉树为空,让该头结点指向自身.
}
BiThrTree pre; //设置前驱结点
//令头结点的左指针指向根结点
pre = (*Thrt);
(*Thrt)->lchild = T;
//开始递归输入线索化
InThreading(T,&pre);
//此时结束了最后一个结点的线索化了,下面的代码把头结点的后继指向了最后一个结点.
//并把最后一个结点的后继也指向头结点,此时树成为了一个类似双向链表的循环.
pre->rchild = *Thrt;
pre->RTag = Thread;
(*Thrt)->rchild = pre;
return OK;
}
遍历线索二叉树
线索二叉树的遍历就可以通过之前建立好的线索,沿着后继线索依依访问下去就行。
//非递归遍历线索二叉树
Status InOrderTraverse(BiThrTree T) {
BiThrNode *p = T->lchild;
while(p!=T){
while(p->LTag==Link) p = p->lchild; //走向左子树的尽头
printf("%c",p->data );
while(p->RTag==Thread && p->rchild!=T) { //访问该结点的后续结点
p = p->rchild;
printf("%c",p->data );
}
p = p->rchild;
}
return OK;
}
森林和二叉树的转换
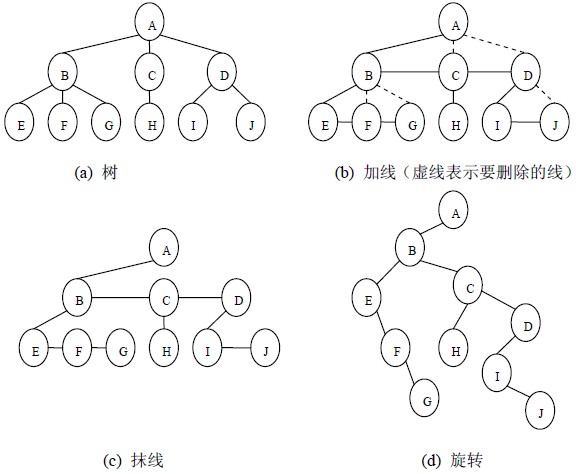
1、树转换为二叉树
由于二叉树是有序的,为了避免混淆,对于无序树,我们约定树中的每个结点的孩子结点按从左到右的顺序进行编号。
将树转换成二叉树的步骤是:
(1)加线。就是在所有兄弟结点之间加一条连线;
(2)抹线。就是对树中的每个结点,只保留他与第一个孩子结点之间的连线,删除它与其它孩子结点之间的连线;
(3)旋转。就是以树的根结点为轴心,将整棵树顺时针旋转一定角度,使之结构层次分明。
树转换为二叉树的过程示意图
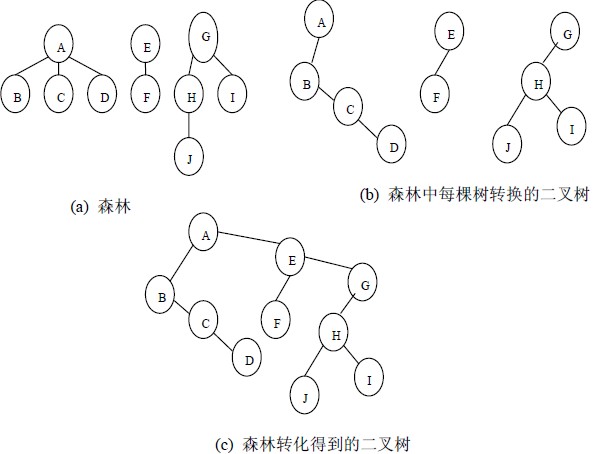
2、森林转换为二叉树
森林是由若干棵树组成,可以将森林中的每棵树的根结点看作是兄弟,由于每棵树都可以转换为二叉树,所以森林也可以转换为二叉树。
将森林转换为二叉树的步骤是:
(1)先把每棵树转换为二叉树;
(2)第一棵二叉树不动,从第二棵二叉树开始,依次把后一棵二叉树的根结点作为前一棵二叉树的根结点的右孩子结点,用线连接起来。当所有的二叉树连接起来后得到的二叉树就是由森林转换得到的二叉树。
森林转换为二叉树的转换过程示意图
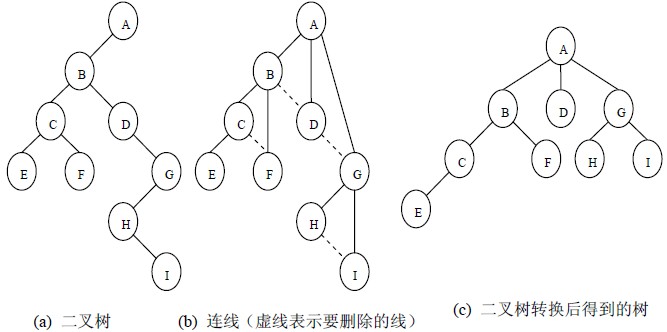
3、二叉树转换为树
二叉树转换为树是树转换为二叉树的逆过程,其步骤是:
(1)若某结点的左孩子结点存在,将左孩子结点的右孩子结点、右孩子结点的右孩子结点……都作为该结点的孩子结点,将该结点与这些右孩子结点用线连接起来;
(2)删除原二叉树中所有结点与其右孩子结点的连线;
(3)整理(1)和(2)两步得到的树,使之结构层次分明。
二叉树转换为树的过程示意图
4、二叉树转换为森林
二叉树转换为森林比较简单,其步骤如下:
(1)先把每个结点与右孩子结点的连线删除,得到分离的二叉树;
(2)把分离后的每棵二叉树转换为树;
(3)整理第(2)步得到的树,使之规范,这样得到森林。
根据树与二叉树的转换关系以及二叉树的遍历定义可以推知,树的先序遍历与其转换的相应的二叉树的先序遍历的结果序列相同;树的后序遍历与其转换的二叉树的中序遍历的结果序列相同;树的层序遍历与其转换的二叉树的后序遍历的结果序列相同。由森林与二叉树的转换关系以及森林与二叉树的遍历定义可知,森林的先序遍历和中序遍历与所转换得到的二叉树的先序遍历和中序遍历的结果序列相同。
哈夫曼树
判定树:
在很多问题的处理过程中,需要进行大量的条件判断,这些判断结构的设计直接影响着程序的执行效率。例如,编制一个程序,将百分制转换成五个等级输出。大家可能认为这个程序很简单,并且很快就可以用下列形式编写出来:
if(score<60)
cout<<"Bad"<<endl;
else if(score<70)
cout<<"Pass"<<endl
else if(score<80)
cout<<"General"<<endl;
else if(score<90)
cout<<"Good"<<endl;
else
cout<<"Very good!"<<endl;
若考虑上述程序所耗费的时间,就会发现该程序的缺陷。在实际中,学生成绩在五个等级上的分布是不均匀的。当学生百分制成绩的录入量很大时,上述判定过程需要反复调用,此时程序的执行效率将成为一个严重问题。
但在实际应用中,往往各个分数段的分布并不是均匀的。下面就是在一次考试中某门课程的各分数段的分布情况:
我们利用哈夫曼树寻找一棵最佳判定树,即总的比较次数最少的判定树。
我们称判定过程最优的二叉树为哈夫曼树,又称最优二叉树
哈夫曼编码
哈夫曼编码(Huffman Coding),又称霍夫曼编码,是一种编码方式,哈夫曼编码是可变字长编码(VLC)的一种。Huffman于1952年提出一种编码方法,该方法完全依据字符出现概率来构造异字头的平均长度最短的码字,有时称之为最佳编码,一般就叫做Huffman编码(有时也称为霍夫曼编码)。
数据的逻辑结构:树状结构。
数据的存储结构设计:
(1)采用静态的三叉链表存放。
算法思想:
申请存储哈夫曼编码串的头指针数组,申请一个字符型指针,用来存放临时的编码串;
从叶子节点开始向上倒退,若其为它双亲节点的左孩子则编码标0,否则标1;直到根节点为止,最后把临时存储编码复制到对应的指针数组所指向的内存中。
重复上述步骤,直到所有的叶子节点都被编码完。
(2)设计一个结构体Element保存哈夫曼树中各结点的信息:
struct Element //哈夫曼树结点的结构体
{
char ch; //字符
int weight; //结点权值
int parent; //双亲指针
int lchild; //左孩子指针
int rchild; //右孩子指针
};
示意图:
weight
ch
Lchild
Rchild
parent
编码表节点结构:
Struct HCode
{
char data; //字符
char code[100]; //编码内容
};
哈夫曼算法的抽象数据类型定义:
ADT Huffman
DataModel
静态三叉链表存储数据
Operation
Select
输入:哈夫曼树的三叉链表H[]
功能:选择权值最小的两棵树
输出:权值最小的两棵树
Reverse
输入:字符串
功能:倒置字符串
输出:倒置后的字符串
HuffmanTree
输入:哈夫曼树的三叉链表H[],字符的权值w[],字符集的大小n
功能:构建哈夫曼树
输出:无
CreateCodeTable
输入:哈夫曼树的三叉链表H[],哈夫曼编码表的三叉链表HC[],字符集的大小n
功能:给每个字符建立左右孩子
输出:哈夫曼编码表
Decode
输入:二进制编码
功能:解码
输出:解码后的字符串
endADT
5. 编码实现与静态检测
(1)创建哈夫曼树的伪代码如下:
算法:HuffmanTree
输入:需要编译的字符和该字符的权值
输出:哈夫曼树
1.用户输入需要编译的字符和该字符的权值(即其字母的频度);
2.构造哈夫曼算法。设计一个数组H保存哈夫曼树中各结点的信息;
3.数组H初始化,将所有结点的孩子域和双亲域的值初始化为-1;
4.数组H的前n个元素的权值给定值;
5.调用select函数选择权值最小的根结点进行合并,其下标分别为i1,i2;
6.将二叉树i1,i2合并为一棵新的二叉树;
7.共进行n-1次合并,直到剩下一棵二叉树,这棵二叉树就是哈夫曼树;
(2)创建编码表的伪代码如下:
算法:创建编码表
输入:哈夫曼树,编码表结构,字符个数
输出:每个字符的内容、权值、左右节点、双亲结点
1.根据已经创建的哈夫曼树创建编码表;
2.从叶子结点开始判断;
2.1如果当前叶子结点的双亲不是根结点,并且是其双亲的左孩子,则编码为‘0’,否则为‘1’;
2.2然后往上对其双亲进行判断,重复操作,直到每个字符编码完毕;
3.将已经完成的编码调用reserve函数进行倒置;
4.按照“下标n,权值weight,左孩子LChuld,右孩子RChild,双亲parent,字符char;
(3)解码的伪代码如下:
算法:Decode
输入:二进制编码
输出:对应的字符串
1.用户输入要解码的二进制字符串,建立一个字符数组存储输入的二进制字符;
2.创建一个指向待解码的字符串的第1个字符的指针;
3.读取每一个字符。设置一个根结点的指针,从根结点开始判断;
3.1若字符为‘0’,则指向哈夫曼树当前结点的左孩子;
3.2若字符为‘1’,则指向当前结点的右孩子;
3.3直到指针指向的当前结点的左孩子为-1时,输出符合的字母;
4.输出解码结果;
时间复杂度:
1)Select函数,时间复杂度O(n)
2)Reverse函数,时间复杂度O(n)
3)HuffmanTree函数,构造哈夫曼树,时间复杂度O(n!)
4)CreateCodeTable函数,构造和输出哈夫曼编码表,时间复杂度O(n)
5)Decode函数,解码,时间复杂度O(n)
6. 上机调试
#include<iostream>
#include<string>
#include<iomanip>
using namespace std;
struct Element
{
char ch;
int weight;
int lchild, rchild, parent;
};
struct HCode
{
char data;
char code[100];
};
int Select(Element H[], int i) //选择两个最小的
{
int min = 11000;
int min1;
for (int k = 0; k<i; k++)
{
if (H[k].weight<min && H[k].parent == -1)
{
min = H[k].weight;
min1 = k;
}
}
H[min1].parent = 1;
return min1;
}
void Reverse(char c[]) //将字符串倒置
{
int n = 0;
char temp;
while (c[n + 1] != '\0')
{
n++;
}
for (int i = 0; i <= n / 2; i++)
{
temp = c[i];
c[i] = c[n - i];
c[n - i] = temp;
}
}
void HuffmanTree(Element H[], int w[], int n) //构造哈夫曼树
{
int i1 = 0, i2 = 0;
for (int i = 0; i<2 * n - 1; i++)
{
H[i].lchild = -1;
H[i].parent = -1;
H[i].rchild = -1;
}
for (int l = 0; l<n; l++)
{
H[l].weight = w[l];
}
for (int k = n; k<2 * n - 1; k++)
{
int i1 = Select(H, k);
int i2 = Select(H, k);
if (i1>i2)
{
int temp;
temp = i1;
i1 = i2;
i2 = temp;
}
H[i1].parent = k;
H[i2].parent = k;
H[k].weight = H[i1].weight + H[i2].weight;
H[k].lchild = i1;
H[k].rchild = i2;
}
}
void CreateCodeTable(Element H[], HCode HC[], int n) //输出哈弗曼编码表
{
HC = new HCode[n];
for (int i = 0; i<n; i++)
{
HC[i].data = H[i].ch;
int ic = i;
int ip = H[i].parent;
int k = 0;
while (ip != -1)
{
if (ic == H[ip].lchild) //左孩子标'0'
HC[i].code[k] = '0';
else
HC[i].code[k] = '1'; //右孩子标'1'
k++;
ic = ip;
ip = H[ic].parent;
}
HC[i].code[k] = '\0';
Reverse(HC[i].code);
}
cout << setiosflags(ios::left)
<< setw(5) << "n"
<< setw(12) << "weight"
<< setw(12) << "LChild"
<< setw(12) << "RChild"
<< setw(12) << "parent"
<< setw(12) << "char"
<< setw(12) << "code"
<< endl;
for (int i = 0; i<2 * n - 1; i++)
{
if (i<n)
{
cout << setiosflags(ios::left)
<< setw(5) << i
<< setw(12) << H[i].weight
<< setw(12) << H[i].lchild
<< setw(12) << H[i].rchild
<< setw(12) << H[i].parent
<< setw(12) << HC[i].data
<< setw(12) << HC[i].code
<< endl;
}
else
cout << setiosflags(ios::left)
<< setw(5) << i
<< setw(12) << H[i].weight
<< setw(12) << H[i].lchild
<< setw(12) << H[i].rchild
<< setw(12) << H[i].parent
<< setw(12) << "\\0"
<< setw(12) << "\\0"
<< endl;
}
}
void Decode(Element H[], HCode HC[], int n, char *s) //解码函数
{
cout << "解码数据为:";
int i = 2 * (n - 1); //根结点
while (*s != '\0')
{
if (*s == '0')
i = H[i].lchild;
else
i = H[i].rchild;
if (H[i].lchild == -1)
{
cout << H[i].ch;
i = 2 * n - 2;
}
s++;
}
cout << endl;
}
void main()
{
Element H[20];
HCode HC[20];
int n;
int select;
while (1)
{
system("cls");
cout << "\t ******************欢迎使用******************\n";
cout << "\t ***************哈夫曼编码系统***************\n";
cout << "\t *------------------------------------------*\n";
cout << "\t * 1——输入编译字符集 *\n";
cout << "\t * 2——输出编码表 *\n";
cout << "\t * 3——解码 *\n";
cout << "\t * 0——退出 *\n";
cout << "\t *------------------------------------------*\n";
cout << "\t 你要输入的编号是(0--3):";
cin >> select;
if (select == 0) break;
switch (select) {
case 1:
{
cout << endl;
cout << "请输入字符集大小:";
cin >> n;
cout << endl;
char s;
HCode HC[20];
int e[20];
for (int t = 0; t < n; t++)
{
cout << "请输入第" << t + 1 << "个字符:";
cin >> s;
H[t].ch = s;
HC[t].data = H[t].ch;
cout << "请输入该字符的权值:";
cin >> e[t];
cout << endl;
}
HuffmanTree(H, e, n);
system("pause");
break;
}
case 2:
CreateCodeTable(H, HC, n);
system("pause");
break;
case 3:
{
cout << endl;
cout << "请输入解码数据:";
char s[200] = { '\0' };
cin >> s;
Decode(H, HC, n, s);
system("pause");
break;
}
default:
cout << "没有此选项,请重新选择!" << endl;
}
}
}图
1、名词解释:
图(Graph)是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为:G(V,E),其中,G表示一个图,V是图G中顶点的集合,E是图G中边的集合。在图中的数据元素,我们称之为顶点(Vertex),顶点集合有穷非空。在图中,任意两个顶点之间都可能有关系,顶点之间的逻辑关系用边来表示,边集可以是空的。
图按照边的有无方向分为无向图和有向图。无向图由顶点和边组成,有向图由顶点和弧构成。弧有弧尾和弧头之分,带箭头一端为弧头。
图按照边或弧的多少分稀疏图和稠密图。如果图中的任意两个顶点之间都存在边叫做完全图,有向的叫有向完全图。若无重复的边或顶点到自身的边则叫简单图。
图中顶点之间有邻接点、依附的概念。无向图顶点的边数叫做度。有向图顶点分为入度和出度。
图上的边或弧带有权则称为网。
图中顶点间存在路径,两顶点存在路径则说明是连通的,如果路径最终回到起始点则称为环,当中不重复的叫简单路径。若任意两顶点都是连通的,则图就是连通图,有向则称为强连通图。图中有子图,若子图极大连通则就是连通分量,有向的则称为强连通分量。
无向图中连通且n个顶点n-1条边称为生成树。有向图中一顶点入度为0其余顶点入度为1的叫有向树。一个有向图由若干棵有向树构成生成森林。
线性表和树两类数据结构,线性表中的元素是“一对一”的关系,树中的元素是“一对多”的关系,本章所述的图结构中的元素则是“多对多”的关系。图(Graph)是一种复杂的非线性结构,在图结构中,每个元素都可以有零个或多个前驱,也可以有零个或多个后继,也就是说,元素之间的关系是任意的。
2、图的存储结构—-邻接矩阵
图的邻接矩阵的表示方式需要两个数组来表示图的信息,一个一维数组表示每个数据元素的信息,一个二维数组(邻接矩阵)表示图中的边或者弧的信息。
如果图有n个顶点,那么邻接矩阵就是一个n*n的方阵,方阵中每个元素的值的计算公式如下:
邻接矩阵表示图的具体示例如下图所示:
首先给个无向图的实例:
下面是一个有向图的实例:
OK,到这里为止,我们给出一个无向图的邻接矩阵和一个有向图的邻接矩阵,我们可以从这两个邻接矩阵得出一些结论:
无向图的邻接矩阵都是沿对角线对称的
要知道无向图中某个顶点的度,其实就是这个顶点vi在邻接矩阵中第i行或(第i列)的元素之和;
对于有向图,要知道某个顶点的出度,其实就是这个顶点vi在邻接矩阵中第i行的元素之和,如果要知道某个顶点的入度,那就是第i列的元素之和。
但是,如果我们需要表示的图是一个网的时候,例如假设有个图有n个顶点,同样该网的邻接矩阵也是一个n*n的方阵,只是方阵元素的值的计算方式不同,如下图所示:
这里的wij表示两个顶点vi和vj边上的权值。无穷大表示一个计算机允许的、大于所有边上权值的值,也就是一个不可能的极限值。下面是具体示例,表示的一个有向网的图和邻接矩阵:
3、图的存储结构—-邻接矩阵的代码实现
#include<iostream>
using namespace std;
enum Graphkind{ DG, DN, UDG, UDN }; //{有向图,无向图,有向网,无向网}
typedef struct Node
{
int * vex; //顶点数组
int vexnum; //顶点个数
int edge; //图的边数
int ** adjMatrix; //图的邻接矩阵
enum Graphkind kind;
}MGraph;
void createGraph(MGraph & G,enum Graphkind kind)
{
cout << "输入顶点的个数" << endl;
cin >> G.vexnum;
cout << "输入边的个数" << endl;
cin >> G.edge;
//输入种类
//cout << "输入图的种类:DG:有向图 DN:无向图,UDG:有向网,UDN:无向网" << endl;
G.kind = kind;
//为两个数组开辟空间
G.vex = new int[G.vexnum];
G.adjMatrix = new int*[G.vexnum];
cout << G.vexnum << endl;
int i;
for (i = 0; i < G.vexnum; i++)
{
G.adjMatrix[i] = new int[G.vexnum];
}
for (i = 0; i < G.vexnum; i++)
{
for (int k = 0; k < G.vexnum; k++)
{
if (G.kind == DG || G.kind == DN)
{
G.adjMatrix[i][k] = 0;
}
else {
G.adjMatrix[i][k] = INT_MAX;
}
}
}
/*//输入每个元素的信息,这个信息,现在还不需要使用
for (i = 0; i < G.vexnum; i++)
{
cin >> G.vex[i];
}*/
cout << "请输入两个有关系的顶点的序号:例如:1 2 代表1号顶点指向2号顶点" << endl;
for (i = 0; i < G.edge; i++)
{
int a, b;
cin >> a;
cin >> b;
if (G.kind == DN) {
G.adjMatrix[b - 1][a - 1] = 1;
G.adjMatrix[a - 1][b - 1] = 1;
}
else if (G.kind == DG)
{
G.adjMatrix[a - 1][b - 1] = 1;
}
else if (G.kind == UDG)
{
int weight;
cout << "输入该边的权重:" << endl;
cin >> weight;
G.adjMatrix[a - 1][b - 1] = weight;
}
else {
int weight;
cout << "输入该边的权重:" << endl;
cin >> weight;
G.adjMatrix[b - 1][a - 1] = weight;
G.adjMatrix[a - 1][b - 1] = weight;
}
}
}
void print(MGraph g)
{
int i, j;
for (i = 0; i < g.vexnum; i++)
{
for (j = 0; j < g.vexnum; j++)
{
if (g.adjMatrix[i][j] == INT_MAX)
cout << "∞" << " ";
else
cout << g.adjMatrix[i][j] << " ";
}
cout << endl;
}
}
void clear(MGraph G)
{
delete G.vex;
G.vex = NULL;
for (int i = 0; i < G.vexnum; i++)
{
delete G.adjMatrix[i];
G.adjMatrix[i] = NULL;
}
delete G.adjMatrix;
}
int main()
{
MGraph G;
cout << "有向图例子:" << endl;
createGraph(G, DG);
print(G);
clear(G);
cout << endl;
cout << "无向图例子:" << endl;
createGraph(G, DN);
print(G);
clear(G);
cout << endl;
cout << "有向图网例子:" << endl;
createGraph(G, UDG);
print(G);
clear(G);
cout << endl;
cout << "无向图网例子:" << endl;
createGraph(G, UDN);
print(G);
clear(G);
cout << endl;
return 0;
}4、图的存储结构—-邻接矩阵的优缺点
优点:
直观、容易理解,可以很容易的判断出任意两个顶点是否有边,最大的优点就是很容易计算出各个顶点的度。
缺点:
当我么表示完全图的时候,邻接矩阵是最好的表示方法,但是对于稀疏矩阵,由于它边少,但是顶点多,这样就会造成空间的浪费。
5、 图的存储结构—邻接表
邻接表是图的一种链式存储结构。主要是应对于邻接矩阵在顶点多边少的时候,浪费空间的问题。它的方法就是声明两个结构。如下图所示:
OK,我们虽然知道了邻接表是这两个结构来表示图的,那么它的怎么表示的了,不急,我们先把它转为c++代码先,然后,再给个示例,你就明白了。
typedef char Vertextype;
//表结点结构
struct ArcNode {
int adjvex; //某条边指向的那个顶点的位置(一般是数组的下标)。
ArcNode * nextarc; //指向下一个表结点
int weight; //这个只有网图才需要使用。普通的图可以直接忽略
};
//头结点
struct Vnode
{
Vertextype data; //这个是记录每个顶点的信息(现在一般都不需要怎么使用)
ArcNode * firstarc; //指向第一条依附在该顶点边的信息(表结点)
};
无向图的示例:
从图中我们可以知道,顶点是通过一个头结点类型的一维数组来保存的,其中我们每个头结点的firstarc都是指向第一条依附在该顶点边的信息,表结点的adjvex表示的该边的另外一个顶点在顶点数组中的下标,weight域对于普通图是无意义的,可以忽略,nextarc指向的是下一条依附在该顶点的边的信息。
下面再给出一个有向图的例子:
通过上述的两个例子,我们应该明白邻接表是如何进行表示图的信息的了。
6、图的存储结构—-邻接表的代码实现
#include<iostream>
#include<string>
using namespace std;
typedef string Vertextype;
//表结点结构
struct ArcNode {
int adjvex; //某条边指向的那个顶点的位置(一般是数组的下标)。
ArcNode * nextarc; //指向下一个表结点
int weight; //这个只有网图才需要使用。
};
//头结点
struct Vnode
{
Vertextype data; //这个是记录每个顶点的信息(现在一般都不需要怎么使用)
ArcNode * firstarc; //指向第一条依附在该顶点边的信息(表结点)
};
//
struct Graph
{
int kind; //图的种类(有向图:0,无向图:1,有向网:2,无向网:3)
int vexnum; //图的顶点数
int edge; //图的边数
Vnode * node; //图的(顶点)头结点数组
};
void createGraph(Graph & g,int kind)
{
cout << "请输入顶点的个数:" << endl;
cin >> g.vexnum;
cout << "请输入边的个数(无向图/网要乘2):" << endl;
cin >> g.edge;
g.kind = kind; //决定图的种类
g.node = new Vnode[g.vexnum];
int i;
cout << "输入每个顶点的信息:" << endl;//记录每个顶点的信息
for (i = 0; i < g.vexnum; i++)
{
cin >> g.node[i].data;
g.node[i].firstarc=NULL;
}
cout << "请输入每条边的起点和终点的编号:" << endl;
for (i = 0; i < g.edge; i++)
{
int a;
int b;
cin >> a; //起点
cin >> b; //终点
ArcNode * next=new ArcNode;
next->adjvex = b - 1;
if(kind==0 || kind==1)
next->weight = -1;
else {//如果是网图,还需要权重
cout << "输入该边的权重:" << endl;
cin >> next->weight;
}
next->nextarc = NULL;
//将边串联起来
if (g.node[a - 1].firstarc == NULL) {
g.node[a - 1].firstarc=next;
}
else
{
ArcNode * p;
p = g.node[a - 1].firstarc;
while (p->nextarc)//找到该链表的最后一个表结点
{
p = p->nextarc;
}
p->nextarc = next;
}
}
}
void print(Graph g)
{
int i;
cout << "图的邻接表为:" << endl;
for (i = 0; i < g.vexnum; i++)
{
cout << g.node[i].data<<" ";
ArcNode * now;
now = g.node[i].firstarc;
while (now)
{
cout << now->adjvex << " ";
now = now->nextarc;
}
cout << endl;
}
}
int main()
{
Graph g;
cout << "有向图的例子" << endl;
createGraph(g,0);
print(g);
cout << endl;
cout << "无向图的例子" << endl;
createGraph(g, 1);
print(g);
cout << endl;
return 0;
}
7、图的存储结构—-邻接表的优缺点
优点:
对于,稀疏图,邻接表比邻接矩阵更节约空间。
缺点:
不容易判断两个顶点是有关系(边),顶点的出度容易,但是求入度需要遍历整个邻接表。
8、有向图的存储结构—-十字链表
十字链表是有向图的一个专有的链表结构,我们之前也说了,邻接表对于我们计算顶点的入度是一个很麻烦的事情,而十字链表正好可以解决这个问题。十字链表和邻接表一样,他会有两个结构来表示图:其中一个结构用于保存顶点信息,另外一个结构是用于保存每条边的信息,如下图所示:
同样,我们知道头结点就是用于保存每个顶点信息的结构,其中data主要是保存顶点的信息(如顶点的名称),firstin是保存第一个入度的边的信息,firstout保存第一个出度的边的信息。其中,表结点就是记录每条边的信息,其中tailvex是记录这条边弧头的顶点的在顶点表中的下标(不是箭头那个),headvex则是记录弧尾对应的那个顶点在顶点表中的下标(箭头的那个),hlink是指向具有下一个具有相同的headvex的表结点,tlink指向具有相同的tailvex的表结点,weight是表示边的权重(网图才需要使用)。具体的代码表示如下:
typedef string Vertextype;
//表结点结构
struct ArcNode {
int tailvex; //弧尾的下标,一般都是和对应的头结点下标相同
int headvex; //弧头的下标
ArcNode * hlink; //指向下一个弧头同为headvex的表结点 ,边是箭头的那边
ArcNode * tlink; //指向下一个弧尾为tailvex的表结点,边不是箭头的那边
int weight; //只有网才会用这个变量
};
//头结点
struct Vnode
{
Vertextype data; //这个是记录每个顶点的信息(现在一般都不需要怎么使用)
ArcNode *firstin; //指向第一条(入度)在该顶点的表结点
ArcNode *firstout; //指向第一条(出度)在该顶点的表结点
};
下面,我们给出一个有向图的十字链表的例子:
其实,这个自己也可以去尝试手画一个十字链表出来,其实都是很简单的
9、有向图的存储结构—-十字链表代码实现
#include<iostream>
#include<string>
using namespace std;
typedef string Vertextype;
//表结点结构
struct ArcNode {
int tailvex; //弧尾的下标,一般都是和对应的头结点下标相同
int headvex; //弧头的下标
ArcNode * hlink; //指向下一个弧头同为headvex的表结点 ,边是箭头的那边
ArcNode * tlink; //指向下一个弧尾为tailvex的表结点,边不是箭头的那边
int weight; //只有网才会用这个变量
};
//头结点
struct Vnode
{
Vertextype data; //这个是记录每个顶点的信息(现在一般都不需要怎么使用)
ArcNode *firstin; //指向第一条(入度)在该顶点的表结点
ArcNode *firstout; //指向第一条(出度)在该顶点的表结点
};
struct Graph
{
int kind; //图的种类(有向图:0,有向网:1)
int vexnum; //图的顶点数
int edge; //图的边数
Vnode * node; //图的(顶点)头结点数组
};
void createGraph(Graph & g,int kind)
{
cout << "请输入顶点的个数:" << endl;
cin >> g.vexnum;
cout << "请输入边的个数(无向图/网要乘2):" << endl;
cin >> g.edge;
g.kind = kind; //决定图的种类
g.node = new Vnode[g.vexnum];
int i;
cout << "输入每个顶点的信息:" << endl;//记录每个顶点的信息
for (i = 0; i < g.vexnum; i++)
{
cin >> g.node[i].data;
g.node[i].firstin = NULL;
g.node[i].firstout = NULL;
}
cout << "请输入每条边的起点和终点的编号:" << endl;
for (i = 0; i < g.edge; i++)
{
int a, b;
cin >> a;
cin >> b;
ArcNode * next = new ArcNode;
next->tailvex = a - 1; //首先是弧头的下标
next-> headvex = b - 1; //弧尾的下标
//只有网图需要权重信息
if(kind==0)
next->weight = -1;
else
{
cout << "输入该边的权重:" << endl;
cin >> next->weight;
}
next->tlink = NULL;
next->hlink = NULL;
//该位置的顶点的出度还为空时,直接让你fisrstout指针指向新的表结点
//记录的出度信息
if (g.node[a - 1].firstout == NULL)
{
g.node[a - 1].firstout = next;
}
else
{
ArcNode * now;
now = g.node[a - 1].firstout;
while (now->tlink)
{
now = now->tlink;
}
now->tlink = next;
}
//记录某个顶点的入度信息
if (g.node[b - 1].firstin == NULL)
{
g.node[b - 1].firstin = next;
}
else {
ArcNode * now;
now = g.node[b - 1].firstin;
while (now->hlink)//找到最后一个表结点
{
now = now->hlink;
}
now->hlink = next;//更新最后一个表结点
}
}
}
void print(Graph g)
{
int i;
cout << "各个顶点的出度信息" << endl;
for (i = 0; i < g.vexnum; i++)
{
cout << g.node[i].data << " ";
ArcNode * now;
now = g.node[i].firstout;
while (now)
{
cout << now->headvex << " ";
now = now->tlink;
}
cout << "^" << endl;
}
cout << "各个顶点的入度信息" << endl;
for (i = 0; i < g.vexnum; i++)
{
cout << g.node[i].data << " ";
ArcNode * now;
now = g.node[i].firstin;
while (now)
{
cout << now->tailvex << " ";
now = now->hlink;
}
cout << "^" << endl;
}
}
int main()
{
Graph g;
cout << "有向图的例子" << endl;
createGraph(g, 0);
print(g);
cout << endl;
return 0;
}
10、无向图的存储结构—-邻接多重表
邻接多重表是无向图的另一种链式存储结构。我们之前也说了使用邻接矩阵来存储图比价浪费空间,但是如果我们使用邻接表来存储图时,对于无向图又有一些不便的地方,例如我们需要对一条已经访问过的边进行删除或者标记等操作时,我们除了需要找到表示同一条边的两个结点。这会给我们的程序执行效率大打折扣,所以这个时候,邻接多重表就派上用场啦。
首先,邻接多重表同样是对邻接表的一个改进得到来的结构,它同样需要一个头结点保存每个顶点的信息和一个表结点,保存每条边的信息,他们的结构如下:
其中,头结点的结构和邻接表一样,而表结点中就改变比较大了,其中mark为标志域,例如标志是否已经访问过,ivex和jvex代表边的两个顶点在顶点表中的下标,ilink指向下一个依附在顶点ivex的边,jlink指向下一个依附在顶点jvex的边,weight在网图的时候使用,代表该边的权重。
下面是一个无向图的邻接多重表的实例(自己也可以尝试去画画,具体的原理都是很简单的):
11、无向图的存储结构—-邻接多重表代码实现
#include<iostream>
#include<string>
using namespace std;
//表结点
struct ArcNode
{
int mark; //标志位
int ivex; //输入边信息的那个起点
ArcNode * ilink; //依附在顶点ivex的下一条边的信息
int jvex; //输入边信息的那个终点
ArcNode * jlink; //依附在顶点jvex的下一条边的信息
int weight;
};
//头结点
struct VexNode {
string data; //顶点的信息,如顶点名称
ArcNode * firstedge; //第一条依附顶点的边
};
struct Graph {
int vexnum; //顶点的个数
int edge; //边的个数
VexNode *node; //保存顶点信息
};
void createGraph(Graph & g)
{
cout << "请输入顶点的个数:" << endl;
cin >> g.vexnum;
cout << "请输入边的个数(无向图/网要乘2):" << endl;
cin >> g.edge;
g.node = new VexNode[g.vexnum];
int i;
cout << "输入每个顶点的信息:" << endl;//记录每个顶点的信息
for (i = 0; i < g.vexnum; i++)
{
cin >> g.node[i].data;
g.node[i].firstedge = NULL;
}
cout << "请输入每条边的起点和终点的编号:" << endl;
for (i = 0; i < g.edge; i++)
{
int a, b;
cin >> a;
cin >> b;
ArcNode * next = new ArcNode;
next->mark = 0;
next->ivex = a - 1; //首先是弧头的下标
next->jvex = b - 1; //弧尾的下标
next->weight = -1;
next->ilink = NULL;
next->jlink = NULL;
//更新顶点表a-1的信息
if (g.node[a - 1].firstedge == NULL)
{
g.node[a - 1].firstedge = next;
}
else {
ArcNode * now;
now = g.node[a - 1].firstedge;
while (1) {
if (now->ivex == (a - 1) && now->ilink == NULL)
{
now->ilink = next;
break;
}
else if (now->ivex == (a - 1) && now->ilink != NULL) {
now = now->ilink;
}
else if (now->jvex == (a - 1) && now->jlink == NULL)
{
now->jlink = next;
break;
}
else if (now->jvex == (a - 1) && now->jlink != NULL) {
now = now->jlink;
}
}
}
//更新顶点表b-1
if (g.node[b - 1].firstedge == NULL)
{
g.node[b - 1].firstedge = next;
}
else {
ArcNode * now;
now = g.node[b - 1].firstedge;
while (1) {
if (now->ivex == (b - 1) && now->ilink == NULL)
{
now->ilink = next;
break;
}
else if (now->ivex == (b - 1) && now->ilink != NULL) {
now = now->ilink;
}
else if (now->jvex == (b - 1) && now->jlink == NULL)
{
now->jlink = next;
break;
}
else if (now->jvex == (b - 1) && now->jlink != NULL) {
now = now->jlink;
}
}
}
}
}
void print(Graph g)
{
int i;
for (i = 0; i < g.vexnum; i++)
{
cout << g.node[i].data << " ";
ArcNode * now;
now = g.node[i].firstedge;
while (now)
{
cout << "ivex=" << now->ivex << " jvex=" << now->jvex << " ";
if (now->ivex == i)
{
now = now->ilink;
}
else if (now->jvex == i)
{
now = now->jlink;
}
}
cout << endl;
}
}
int main()
{
Graph g;
createGraph(g);
print(g);
system("pause");
return 0;
}
查找
查找定义:根据给定的某个值,在查找表中确定一个其关键字等于给定值的数据元素(或记录)。
查找算法分类:
1)静态查找和动态查找;
注:静态或者动态都是针对查找表而言的。动态表指查找表中有删除和插入操作的表。
2)无序查找和有序查找。
无序查找:被查找数列有序无序均可;
有序查找:被查找数列必须为有序数列。
平均查找长度(Average Search Length,ASL):需和指定key进行比较的关键字的个数的期望值,称为查找算法在查找成功时的平均查找长度。
对于含有n个数据元素的查找表,查找成功的平均查找长度为:ASL = Pi*Ci的和。
Pi:查找表中第i个数据元素的概率。
Ci:找到第i个数据元素时已经比较过的次数。
1. 顺序查找
说明:顺序查找适合于存储结构为顺序存储或链接存储的线性表。
基本思想:顺序查找也称为线形查找,属于无序查找算法。从数据结构线形表的一端开始,顺序扫描,依次将扫描到的结点关键字与给定值k相比较,若相等则表示查找成功;若扫描结束仍没有找到关键字等于k的结点,表示查找失败。
复杂度分析:
查找成功时的平均查找长度为:(假设每个数据元素的概率相等) ASL = 1/n(1+2+3+…+n) = (n+1)/2 ;
当查找不成功时,需要n+1次比较,时间复杂度为O(n);
所以,顺序查找的时间复杂度为O(n)。
C++实现源码:
//顺序查找
-
int SequenceSearch(int a[], int value, int n) -
{ -
int i; -
for(i=0; i<n; i++) -
if(a[i]==value) -
return i; -
return -1; -
}
2. 二分查找
说明:元素必须是有序的,如果是无序的则要先进行排序操作。
基本思想:也称为是折半查找,属于有序查找算法。用给定值k先与中间结点的关键字比较,中间结点把线形表分成两个子表,若相等则查找成功;若不相等,再根据k与该中间结点关键字的比较结果确定下一步查找哪个子表,这样递归进行,直到查找到或查找结束发现表中没有这样的结点。
复杂度分析:最坏情况下,关键词比较次数为log2(n+1),且期望时间复杂度为O(log2n);
注:折半查找的前提条件是需要有序表顺序存储,对于静态查找表,一次排序后不再变化,折半查找能得到不错的效率。但对于需要频繁执行插入或删除操作的数据集来说,维护有序的排序会带来不小的工作量,那就不建议使用。——《大话数据结构》
C++实现源码:
-
//二分查找(折半查找),版本1 -
int BinarySearch1(int a[], int value, int n) -
{ -
int low, high, mid; -
low = 0; -
high = n-1; -
while(low<=high) -
{ -
mid = (low+high)/2; -
if(a[mid]==value) -
return mid; -
if(a[mid]>value) -
high = mid-1; -
if(a[mid]<value) -
low = mid+1; -
} -
return -1; -
} -
//二分查找,递归版本 -
int BinarySearch2(int a[], int value, int low, int high) -
{ -
int mid = low+(high-low)/2; -
if(low > high) -
return -1; -
if(a[mid]==value) -
return mid; -
if(a[mid]>value) -
return BinarySearch2(a, value, low, mid-1); -
if(a[mid]<value) -
return BinarySearch2(a, value, mid+1, high); -
}
3. 插值查找
在介绍插值查找之前,首先考虑一个新问题,为什么上述算法一定要是折半,而不是折四分之一或者折更多呢?
打个比方,在英文字典里面查“apple”,你下意识翻开字典是翻前面的书页还是后面的书页呢?如果再让你查“zoo”,你又怎么查?很显然,这里你绝对不会是从中间开始查起,而是有一定目的的往前或往后翻。
同样的,比如要在取值范围1 ~ 10000 之间 100 个元素从小到大均匀分布的数组中查找5, 我们自然会考虑从数组下标较小的开始查找。
经过以上分析,折半查找这种查找方式,不是自适应的(也就是说是傻瓜式的)。二分查找中查找点计算如下:
mid=(low+high)/2, 即mid=low+1/2*(high-low);
通过类比,我们可以将查找的点改进为如下:
mid=low+(key-a[low])/(a[high]-a[low])*(high-low),
也就是将上述的比例参数1/2改进为自适应的,根据关键字在整个有序表中所处的位置,让mid值的变化更靠近关键字key,这样也就间接地减少了比较次数。
基本思想:基于二分查找算法,将查找点的选择改进为自适应选择,可以提高查找效率。当然,差值查找也属于有序查找。
注:对于表长较大,而关键字分布又比较均匀的查找表来说,插值查找算法的平均性能比折半查找要好的多。反之,数组中如果分布非常不均匀,那么插值查找未必是很合适的选择。
复杂度分析:查找成功或者失败的时间复杂度均为O(log2(log2n))。
C++实现源码:
//插值查找
int InsertionSearch(int a[], int value, int low, int high)
{
int mid = low+(value-a[low])/(a[high]-a[low])*(high-low);
if(a[mid]==value)
return mid;
if(a[mid]>value)
return InsertionSearch(a, value, low, mid-1);
if(a[mid]<value)
return InsertionSearch(a, value, mid+1, high);
}4. 斐波那契查找
在介绍斐波那契查找算法之前,我们先介绍一下很它紧密相连并且大家都熟知的一个概念——黄金分割。
黄金比例又称黄金分割,是指事物各部分间一定的数学比例关系,即将整体一分为二,较大部分与较小部分之比等于整体与较大部分之比,其比值约为1:0.618或1.618:1。
0.618被公认为最具有审美意义的比例数字,这个数值的作用不仅仅体现在诸如绘画、雕塑、音乐、建筑等艺术领域,而且在管理、工程设计等方面也有着不可忽视的作用。因此被称为黄金分割。
大家记不记得斐波那契数列:1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89…….(从第三个数开始,后边每一个数都是前两个数的和)。然后我们会发现,随着斐波那契数列的递增,前后两个数的比值会越来越接近0.618,利用这个特性,我们就可以将黄金比例运用到查找技术中。
基本思想:也是二分查找的一种提升算法,通过运用黄金比例的概念在数列中选择查找点进行查找,提高查找效率。同样地,斐波那契查找也属于一种有序查找算法。
相对于折半查找,一般将待比较的key值与第mid=(low+high)/2位置的元素比较,比较结果分三种情况:
1)相等,mid位置的元素即为所求
2)>,low=mid+1;
3)<,high=mid-1。
斐波那契查找与折半查找很相似,他是根据斐波那契序列的特点对有序表进行分割的。他要求开始表中记录的个数为某个斐波那契数小1,及n=F(k)-1;
开始将k值与第F(k-1)位置的记录进行比较(及mid=low+F(k-1)-1),比较结果也分为三种
1)相等,mid位置的元素即为所求
2)>,low=mid+1,k-=2;
说明:low=mid+1说明待查找的元素在[mid+1,high]范围内,k-=2 说明范围[mid+1,high]内的元素个数为n-(F(k-1))= Fk-1-F(k-1)=Fk-F(k-1)-1=F(k-2)-1个,所以可以递归的应用斐波那契查找。
3)<,high=mid-1,k-=1。
说明:low=mid+1说明待查找的元素在[low,mid-1]范围内,k-=1 说明范围[low,mid-1]内的元素个数为F(k-1)-1个,所以可以递归 的应用斐波那契查找。
复杂度分析:最坏情况下,时间复杂度为O(log2n),且其期望复杂度也为O(log2n)。
C++实现源码:
-
// 斐波那契查找.cpp #include "stdafx.h" #include <memory> #include <iostream> using namespace std; const int max_size=20;//斐波那契数组的长度 /*构造一个斐波那契数组*/ void Fibonacci(int * F) { F[0]=0; F[1]=1; for(int i=2;i<max_size;++i) F[i]=F[i-1]+F[i-2]; } /*定义斐波那契查找法*/ int FibonacciSearch(int *a, int n, int key) //a为要查找的数组,n为要查找的数组长度,key为要查找的关键字 { int low=0; int high=n-1; int F[max_size]; Fibonacci(F);//构造一个斐波那契数组F int k=0; while(n>F[k]-1)//计算n位于斐波那契数列的位置 ++k; int * temp;//将数组a扩展到F[k]-1的长度 temp=new int [F[k]-1]; memcpy(temp,a,n*sizeof(int)); for(int i=n;i<F[k]-1;++i) temp[i]=a[n-1]; while(low<=high) { int mid=low+F[k-1]-1; if(key<temp[mid]) { high=mid-1; k-=1; } else if(key>temp[mid]) { low=mid+1; k-=2; } else { if(mid<n) return mid; //若相等则说明mid即为查找到的位置 else return n-1; //若mid>=n则说明是扩展的数值,返回n-1 } } delete [] temp; return -1; } int main() { int a[] = {0,16,24,35,47,59,62,73,88,99}; int key=100; int index=FibonacciSearch(a,sizeof(a)/sizeof(int),key); cout<<key<<" is located at:"<<index; return 0; }
5. 树表查找
5.1 最简单的树表查找算法——二叉树查找算法。
基本思想:二叉查找树是先对待查找的数据进行生成树,确保树的左分支的值小于右分支的值,然后在就行和每个节点的父节点比较大小,查找最适合的范围。 这个算法的查找效率很高,但是如果使用这种查找方法要首先创建树。
二叉查找树(BinarySearch Tree,也叫二叉搜索树,或称二叉排序树Binary Sort Tree)或者是一棵空树,或者是具有下列性质的二叉树:
1)若任意节点的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
2)若任意节点的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
3)任意节点的左、右子树也分别为二叉查找树。
二叉查找树性质:对二叉查找树进行中序遍历,即可得到有序的数列。
不同形态的二叉查找树如下图所示:

有关二叉查找树的查找、插入、删除等操作的详细讲解,请移步浅谈算法和数据结构: 七 二叉查找树。
复杂度分析:它和二分查找一样,插入和查找的时间复杂度均为O(logn),但是在最坏的情况下仍然会有O(n)的时间复杂度。原因在于插入和删除元素的时候,树没有保持平衡(比如,我们查找上图(b)中的“93”,我们需要进行n次查找操作)。我们追求的是在最坏的情况下仍然有较好的时间复杂度,这就是平衡查找树设计的初衷。
下图为二叉树查找和顺序查找以及二分查找性能的对比图:

内部排序
内部排序:整个排序过程完全在内存中进行。
常见的十种排序算法: 冒泡排序、选择排序、插入排序、归并排序、快速排序、希尔排序、堆排序、计数排序、桶排序、基数排序
1.冒泡排序(Bubble Sort)也是一种简单直观的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢"浮"到数列的顶端。
作为最简单的排序算法之一,冒泡排序给我的感觉就像 Abandon 在单词书里出现的感觉一样,每次都在第一页第一位,所以最熟悉。冒泡排序还有一种优化算法,就是立一个 flag,当在一趟序列遍历中元素没有发生交换,则证明该序列已经有序。但这种改进对于提升性能来说并没有什么太大作用。
1. 算法步骤
比较相邻的元素。如果第一个比第二个大,就交换他们两个。
对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数。
针对所有的元素重复以上的步骤,除了最后一个。
持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
#include <stdio.h>
void bubble_sort(int arr[], int len) {
int i, j, temp;
for (i = 0; i < len - 1; i++)
for (j = 0; j < len - 1 - i; j++)
if (arr[j] > arr[j + 1]) {
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
int main() {
int arr[] = { 22, 34, 3, 32, 82, 55, 89, 50, 37, 5, 64, 35, 9, 70 };
int len = (int) sizeof(arr) / sizeof(*arr);
bubble_sort(arr, len);
int i;
for (i = 0; i < len; i++)
printf("%d ", arr[i]);
return 0;
}
2.选择排序
选择排序是一种简单直观的排序算法,无论什么数据进去都是 O(n²) 的时间复杂度。所以用到它的时候,数据规模越小越好。唯一的好处可能就是不占用额外的内存空间了吧。
1. 算法步骤
首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置。
再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。
重复第二步,直到所有元素均排序完毕。
void swap(int *a,int *b) //交換两个变量
{
int temp = *a;
*a = *b;
*b = temp;
}
void selection_sort(int arr[], int len)
{
int i,j;
for (i = 0 ; i < len - 1 ; i++)
{
int min = i;
for (j = i + 1; j < len; j++) //走访未排序的元素
if (arr[j] < arr[min]) //找到目前最小值
min = j; //记录最小值
swap(&arr[min], &arr[i]); //做交換
}
}
3.插入排序
插入排序的代码实现虽然没有冒泡排序和选择排序那么简单粗暴,但它的原理应该是最容易理解的了,因为只要打过扑克牌的人都应该能够秒懂。插入排序是一种最简单直观的排序算法,它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
插入排序和冒泡排序一样,也有一种优化算法,叫做拆半插入。
1. 算法步骤
将第一待排序序列第一个元素看做一个有序序列,把第二个元素到最后一个元素当成是未排序序列。
从头到尾依次扫描未排序序列,将扫描到的每个元素插入有序序列的适当位置。(如果待插入的元素与有序序列中的某个元素相等,则将待插入元素插入到相等元素的后面。)void insertion_sort(int arr[], int len){
int i,j,key;
for (i=1;i<len;i++){
key = arr[i];
j=i-1;
while((j>=0) && (arr[j]>key)) {
arr[j+1] = arr[j];
j--;
}
arr[j+1] = key;
}
}
4. 希尔排序
希尔排序,也称递减增量排序算法,是插入排序的一种更高效的改进版本。但希尔排序是非稳定排序算法。
希尔排序是基于插入排序的以下两点性质而提出改进方法的:
- 插入排序在对几乎已经排好序的数据操作时,效率高,即可以达到线性排序的效率;
- 但插入排序一般来说是低效的,因为插入排序每次只能将数据移动一位;
希尔排序的基本思想是:先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,待整个序列中的记录"基本有序"时,再对全体记录进行依次直接插入排序。
1. 算法步骤
选择一个增量序列 t1,t2,……,tk,其中 ti > tj, tk = 1;
按增量序列个数 k,对序列进行 k 趟排序;
每趟排序,根据对应的增量 ti,将待排序列分割成若干长度为 m 的子序列,分别对各子表进行直接插入排序。仅增量因子为 1 时,整个序列作为一个表来处理,表长度即为整个序列的长度。
void shell_sort(int arr[], int len) {
int gap, i, j;
int temp;
for (gap = len >> 1; gap > 0; gap >>= 1)
for (i = gap; i < len; i++) {
temp = arr[i];
for (j = i - gap; j >= 0 && arr[j] > temp; j -= gap)
arr[j + gap] = arr[j];
arr[j + gap] = temp;
}
}
5.归并排序
归并排序(Merge sort)是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。
作为一种典型的分而治之思想的算法应用,归并排序的实现由两种方法:
- 自上而下的递归(所有递归的方法都可以用迭代重写,所以就有了第 2 种方法);
- 自下而上的迭代;
在《数据结构与算法 JavaScript 描述》中,作者给出了自下而上的迭代方法。但是对于递归法,作者却认为:
However, it is not possible to do so in JavaScript, as the recursion goes too deep for the language to handle.
然而,在 JavaScript 中这种方式不太可行,因为这个算法的递归深度对它来讲太深了。
说实话,我不太理解这句话。意思是 JavaScript 编译器内存太小,递归太深容易造成内存溢出吗?还望有大神能够指教。
和选择排序一样,归并排序的性能不受输入数据的影响,但表现比选择排序好的多,因为始终都是 O(nlogn) 的时间复杂度。代价是需要额外的内存空间。
2. 算法步骤
int min(int x, int y) return x < y ? x : y;}void merge_sort(int arr[], int len) {
int *a = arr;
int *b = (int *) malloc(len * sizeof(int));
int seg, start;
for (seg = 1; seg < len; seg += seg) {
for (start = 0; start < len; start += seg * 2) {
int low = start, mid = min(start + seg, len), high = min(start + seg * 2, len);
int k = low;
int start1 = low, end1 = mid;
int start2 = mid, end2 = high;
while (start1 < end1 && start2 < end2)
b[k++] = a[start1] < a[start2] ? a[start1++] : a[start2++];
while (start1 < end1)
b[k++] = a[start1++];
while (start2 < end2)
b[k++] = a[start2++];
}
int *temp = a;
a = b;
b = temp;
}
if (a != arr) {
int i;
for (i = 0; i < len; i++)
b[i] = a[i];
b = a;
}
free(b);
}
-
申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列;
-
设定两个指针,最初位置分别为两个已经排序序列的起始位置;
-
比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置;
-
重复步骤 3 直到某一指针达到序列尾;
-
将另一序列剩下的所有元素直接复制到合并序列尾。
6.快速排序
快速排序是由东尼·霍尔所发展的一种排序算法。在平均状况下,排序 n 个项目要 Ο(nlogn) 次比较。在最坏状况下则需要 Ο(n2) 次比较,但这种状况并不常见。事实上,快速排序通常明显比其他 Ο(nlogn) 算法更快,因为它的内部循环(inner loop)可以在大部分的架构上很有效率地被实现出来。
快速排序使用分治法(Divide and conquer)策略来把一个串行(list)分为两个子串行(sub-lists)。
快速排序又是一种分而治之思想在排序算法上的典型应用。本质上来看,快速排序应该算是在冒泡排序基础上的递归分治法。
快速排序的名字起的是简单粗暴,因为一听到这个名字你就知道它存在的意义,就是快,而且效率高!它是处理大数据最快的排序算法之一了。虽然 Worst Case 的时间复杂度达到了 O(n²),但是人家就是优秀,在大多数情况下都比平均时间复杂度为 O(n logn) 的排序算法表现要更好,可是这是为什么呢,我也不知道。好在我的强迫症又犯了,查了 N 多资料终于在《算法艺术与信息学竞赛》上找到了满意的答案:
快速排序的最坏运行情况是 O(n²),比如说顺序数列的快排。但它的平摊期望时间是 O(nlogn),且 O(nlogn) 记号中隐含的常数因子很小,比复杂度稳定等于 O(nlogn) 的归并排序要小很多。所以,对绝大多数顺序性较弱的随机数列而言,快速排序总是优于归并排序。
1. 算法步骤
-
从数列中挑出一个元素,称为 "基准"(pivot);
-
重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作;
-
递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序;
typedef struct _Range {
int start, end;
} Range;
Range new_Range(int s, int e) {
Range r;
r.start = s;
r.end = e;
return r;
}
void swap(int *x, int *y) {
int t = *x;
*x = *y;
*y = t;
}
void quick_sort(int arr[], const int len) {
if (len <= 0)
return; // 避免len为负值引发错误(Segment Fault)
// r[]模拟列表,p为数量,r[p++]为push操作,r[p--]为pop操作且可以取得元素
Range r[len];
int p = 0;
r[p++] = new_Range(0, len - 1);
while (p) {
Range range = r[--p];
if (range.start >= range.end)
continue;
int mid = arr[(range.start + range.end) / 2]; // 选取中间点为基准点
int left = range.start, right = range.end;
do {
while (arr[left] < mid) ++left; // 检查基准点左侧是否符合要求
while (arr[right] > mid) --right; //检测基准点右侧是否符合要求
if (left <= right) {
swap(&arr[left], &arr[right]);
left++;
right--; // 移动指针以继续
}
} while (left <= right);
if (range.start < right) r[p++] = new_Range(range.start, right);
if (range.end > left) r[p++] = new_Range(left, range.end);
}
}





















 572
572











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








