数据结构--向量--向量介绍

最新推荐文章于 2024-09-10 18:28:47 发布

置顶 LazyChun

最新推荐文章于 2024-09-10 18:28:47 发布

阅读量1.2w

点赞数 8

分类专栏：数据结构学习 C++学习数据结构（C++）

本文链接：https://blog.csdn.net/u014581901/article/details/50083433

版权

C++学习同时被 3 个专栏收录

17 篇文章 1 订阅

订阅专栏

数据结构（C++）

8 篇文章 2 订阅

订阅专栏

数据结构学习

7 篇文章 0 订阅

订阅专栏

本页内容：

   1.向量介绍
   2.向量的抽象数据类型接口

     3.ADT接口函数辅助函数

     4.ADT接口函数操作实例

     5.向量模板实现源码

     6.ADT接口函数实现及算法讲解

     7.ADT接口函数辅助函数实现及算法讲解

     8.向量的运算符重载

1.向量介绍

向量是数组的抽象与泛化，由一组元素由线性次序封装而成。各元素与其相应的秩(rank)一一对应，采用循秩访问(call-by-rank)的方式，使对各元素的操作，管理维护更加简化、统一与安全。向量的元素类型可以灵活选取，便于定制复杂的数据结构。

2.向量的抽象数据类型接口（ADT接口）

ADT=Abstract Data Type

向量要完成一些工作，需要有相应的接口函数，我们先来总体浏览一下这些接口函数，及其所需要完成的功能。

3.ADT接口函数辅助函数

要实现上述ADT接口函数，我们还需要一些函数的帮助。毕竟控制向量大小等这些小事也要麻烦我伟大的接口函数就不好了。

这些函数有哪些呢？我们先来总体看一下：

对，就是这些在protected中的函数，它们不会直接被使用向量的开发者使用，它们只是被ADT接口函数使用。我们后面将介绍它们的实现。

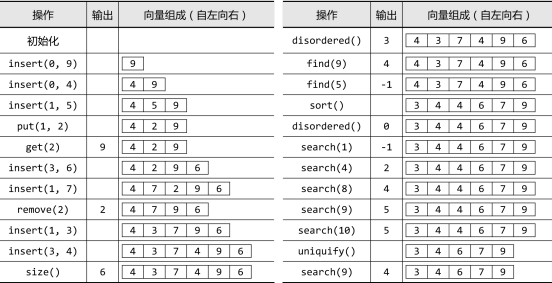
4.ADT接口函数操作实例

我们现在再来形象地看一下接口函数的具体操作过程。

5.向量模板实现源码

自己写了一个向量模板，由于代码过多，不适合都在此页展示，于是写在了另外一篇博文里。下面是博文链接：

向量模板源码

大家也可以直接下载：

myVector

6.ADT接口函数实现及算法讲解

typedef int Rank; //我们先用Rank(秩)代替int,毕竟向量的下标是秩(Rank)嘛！

size函数：

size()

其作用是返回当前向量的大小，及向量中所存在元素的总个数。其实现比较简单，我们只需用一个整形(int)变量 _size来跟踪向量的大小变化，记录向量的。 size()函数只需返回 _size的值即可。

代码实现：

template<typename T>
Rank myVector<T>::size() const 
{
	return _size;
}

get函数：

get(Rank r)

其作用是获取向量中秩为r的元素并返回其值。

代码实现：

template<typename T>
T myVector<T>::get(Rank r) const
{
	return _elem[r];
}

put函数：

put(Rank r,T e)

其作用是用e替换向量中秩为r的元素的值。
代码实现：

template<typename T>
void myVector<T>::put(Rank r,T e)
{
	_elem[r]=e;//用e替换秩为r的数值 
}

insert函数：

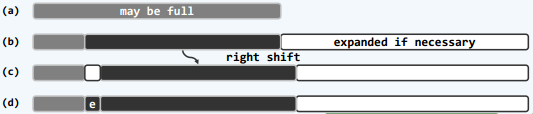
insert(Rank r,T cosnt & e)

其作用是在向量秩为r及r以后的元素依次后移一位然后将e插入r处。可形象的如下图表示：

代码实现：

template<typename T>
Rank myVector<T>::insert(Rank r,T const& e)
{
	expand();//如果有必要，扩容
	for(int i=_size;i>r;i--)//自后向前 
	{
	   _elem[i]=_elem[i-1];//后继元素顺次后移一个单元 	
	} 
	_elem[r]=e;//置入新元素 
	_size++;// 更新容量 
	return r;//返回秩  
}<span style="font-family: Arial, Helvetica, sans-serif; background-color: rgb(255, 255, 255);">   </span>

remove函数：

remove(Rank lo,Rank,hi)

其作用是删除向量中秩在区间[lo,hi)之间的所有元素。即将秩在区间[hi,n)间的元素向前移动(hi-lo)位，其返回值为被删除元素的数目。可形象地如下图表示：

代码实现：

template<typename T>
int myVector<T>::remove(Rank lo,Rank hi)
{
  	if(lo==hi)
	{
	  return 0;
	}
    while(hi<_size)
    {
	 _elem[lo++]=_elem[hi++];//[hi,_size)顺次前移hi-lo位 
    }
    _size=lo;//更新规模 
    shrink();// 如有必要，缩容 
    return hi-lo;//返回被删除元素的数目
}

remove(Rank r)

其是remove(Rank lo,Rank hi)函数的特殊版，即为remove(Rank r,Rank r+1)。为了删除一个元素时操作方便将其重载为此简单形式。其返回值为被删除元素的值。

代码实现：

template<typename T>
T myVector<T>::remove(Rank r)
{
  	T e=_elem[r];
        remove(r,r+1);
        return e;
}

disordered函数：

disordered()

其作用是判断向量中所有元素是否已按非降序排列，是则会返回0，不是则返回相邻元素的逆序对数。

代码实现：

template<typename T>
int myVector<T>::disordered() const
{
	int n=0;//计数器
	for(int i=1;i<_size;i++)//逐一检查各对相邻元素 
	{
	  n+=(_elem[i-1]>_elem[i]);//逆序则计数 
	} 
	return n;//向量有序当且仅当n=0 
}

sort函数：

sort(Rank lo,Rank hi)

其作用是将向量中秩在区间[lo,hi)间的所有元素按非降序排列。其实现由很多种算法，如起泡排序，快数排序等等。但无论是何种算法，其接口必须与sort函数一致。我们将在另外的博文里详细介绍。以下给出博文链接：

起泡排序(bubbleSort)

归并排序(mergeSort)

快速排序(quickSort)

选择排序(selectionSort)

堆排序 (heapSort)

sort()

其为sort(Rank lo,Rank hi)函数的特殊版，即sort[0,n)将向量的所有元素按非降序排列。

函数实现：

template<typename T>
void myVector<T>::sort()
{
	sort(0,_size);
}

find函数

find(T const & e,Rank lo,Rank hi)

其作用是在秩在区间[lo,hi)间的这些元素中，从后向前查找向量中值为e的元素，并返回其秩。因为是从后向前查找，所以它找到的总是在区间[lo,hi)中秩最大的值为e的那个元素。这正是我们规定的返回值。若没找到，则返回(lo-1)。它属于傻瓜式的硬查找，耗费时间较多，适用于有序与无序向量。但有序向量还有跟聪明的查找放法，一般不会用它，我们后面会讲到。

函数实现：

template<typename T>
Rank myVector<T>::find( T const& e, Rank lo, Rank hi ) const//在向量中查找元素，并返回秩最大者 
{
	while((lo<hi--)&&e!=_elem[hi]) ;//逆向查找 
 	return hi;//hi<lo意味着失败；否则hi即命中元素的秩 
}

find(T const & e)

其为find(T const &e,Rank lo,Rank hi)函数的特殊版，即find(e,o,n)，范围为全局。

函数实现：

template<typename T>
Rank myVector<T>::find( T const& e ) const//在向量中查找元素，并返回秩最大者 
{
	while((lo<hi--)&&e!=_elem[hi]) ;//逆向查找 
 	return hi;//hi<lo意味着失败；否则hi即命中元素的秩 
}

search函数：

search(T const &e,Rank lo,Rank hi)

其为用于有序向量的查找函数，因为有序向量的一些特性，使其有更加快捷的查找方法，如二分查找等。其返回值为向量中秩在区间[lo,hi)中的所有元素中值不大于e 且秩最大的元素。我们将在另外的博文里详细介绍它的几种快捷查找算法。下面给出博文链接：

二分查找（binSearch)

斐波拉契查找(fibSearch)

search(T const &e)

其为search(T const &e,Rank lo,Rank hi)函数的特殊版，即search(e,0,n)全局查找。

代码实现：

template<typename T>
Rank myVector<T>::search(T const &e) const
{
	return search(e,0,_size);
}

deduplicate函数

deduplicate()

其作用是剔除重复元素，并返回剔除的重复元素个数。可作用于无序与有序向量，效率较低。

template<typename T>
int myVector<T>::deduplicate()
{
	int oldSize=_size;//记录原规模
	Rank i=1;//从_elem[1]开始
	while(i<_size)//自前向后逐一考查各元素_elem[i] 
	{
	  if(find(_elem[i],0,i)<0)//在前缀中寻找雷同者 
	  {
	      i++;//若无雷同则继续考查其后继
	  } 
	  else
	  {
	   remove(i);//否则删除雷同者  
      }
	}
    return oldSize-_size;//向量规模变化量。即删除元素总数	
}

uniquify函数

uniquify()
其做用是剔除有序向量的重复元素，并返回剔除重复元素的个数。由于有序向量的性质，去重算法的效率可以大大提高。下面给出两种算法：
低效算法：在有序向量中，重复元素必然相互紧邻构成一个区间，因此每个区间只需保留一个元素即可。其他统统删除。

代码实现：

    template<typename T>
    int Vector<T>::uniquify() 
    {
    	int oldSize=_size;
    	int i=0;//从首元素开始 
        while(i<_size-1)//从前向后逐一比对各队相邻元素 
    	{
    		(_elem[i]==_elem[i+1])?remove(i+1):i++;//若雷同，则删除后者；否则转至后后一元素 
		}
		return oldSize-_size;//向量规模变化量。即删除元素总数
	}

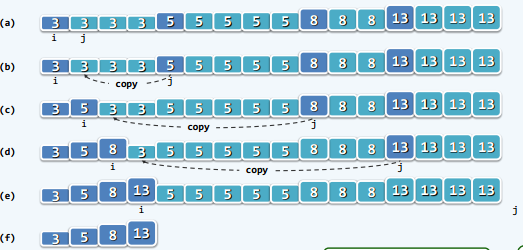
高效算法：上述低效算法之所以低效，是因为要多次执行remove函数，每执行一次remove，都要将后继元素依次前移，导致复杂度增加。由此可想，我们何不去掉 remove函数，直接在每个区间中取出一个元素组成一个新的向量呢。可用下图形象展示。

代码实现：

	template<typename T>
	int Vector<T>::uniquify()
	{ 
		Rank i=0,j=0;//各对互异"相邻"元素的秩
		while(++j<_size)//逐一扫描，直至末元素 
		{
			if(_elem[i]!=_elem[j]) _elem[++i]=_elem[j];//跳过雷同者；发现不同元素时，向前移至紧邻于前者右侧 
			
		 } 
		 _size=++i;shrink();//直接截除尾部多于元素 
		 return j-i;//向量规模变化量。即删除元素总数
	 }

traverser函数

traverser()

其作用是遍历向量所用元素并统一对其进行相关操作。可利用对象机制或函数指针来实现。
代码实现：

//遍历1--利用函数指针进行只读或局部性修改
template<typename T>
void myVector<T>::traverse(void (*visit ) ( T& )) 
{
	for(int i=0;i<_size;i++)
	{
		visit(_elem[i]);
	}
}
//遍历2--利用对象机制可进行全局性修改
template<typename T>
template<typename VST>
void myVector<T>::traverse(VST &visit)
{
	for(int i=0;i<_size;i++)
	{
		visit(_elem[i]);
	}
}

7.ADT接口函数辅助函数实现及算法讲解

copyFrom函数

copyFrom(T const *A,Rank lo,Rank hi)

其作用是复制数字A在区间[lo,hi)间元素的值到本向量的数组_elem中。即向量初始赋值时所用，一般用在向量的构造函数里。

代码实现：

template<typename T>
void myVector<T>::copyFrom(T const*A,Rank lo,Rank hi)
{
	_size=hi-lo;//获取向量规模
	_capacity=hi-lo;//获取向量容量
	_elem=new T[_capacity];//生成向量数据区(此时向量处于饱和状态） 
	for(int i=lo;i<hi;i++)
	{
		_elem[i-lo]=A[i];
	}
}

expand函数

expand()

其作用是管理向量空间，自动判断向量空间是否足够，如果不足，则自动扩容，扩大一倍。

代码实现：

template<typename T>
void myVector<T>::expand()
{
 	if(_size<_capacity)
	{
	 	return;	//尚未满员时，不必扩容
	} 
	_capacity=maxoftwo(_capacity,DEFAULT_CAPACITY);//不低于最小容量
	T*oldElem=_elem;//原向量指针保存 
	_elem=new T[_capacity<<=1];//容量加倍
	for(int i=0;i<_size;i++)//复制原向量内容 
	{
		_elem[i]=oldElem[i];//T为基本类型 ，或已重载赋值操作符"=" 
	} 
	delete [] oldElem;//释放原空间 
}

shrink函数

shrink()

其所用也是管理向量空间，如果空间的利用率低于一半，则自动缩容，缩小一半，节约空间。

代码实现：

template<typename T>
void myVector<T>::shrink()
{
	if(_size<_capacity/2)
	{
		T*oldElem=_elem;//原向量指针保存
		_elem=new T[_capacity>>=1];//容量缩减一半 
		for(int i=0;i<_size;i++)//复制原向量内容
		{
			_elem[i]=oldElem[i];
		} 
	}
}

max函数

max(Rank lo,Rank hi)

其作用是找到向量秩在区间[lo,hi)里的所有元素中值最大的元素，并返回其秩。

代码实现：

template<typename T>
Rank myVector<T>::max(Rank lo,Rank hi)
{
	T maxT;
	Rank rank;
	maxT=_elem[lo];
	for(int i=lo;i<hi;i++)
	{
		if(maxT<_elem[i])
		{
			rank=i;
			maxT=_elem[i];
		}
	} 
	return rank;
}

maxoftwo函数

maxoftwo(int one,int two)

其作用是返回量对象中最大的那个。

代码实现：

template<typename T>
int myVector<T>::max(int one,int two)
{
	if(one>two)
        {
            return one;
          }
         else
         {
            return two;
           }
}

8.向量的运算符重载

我们用向量的时候，有时候觉得V.add()、V.get()的这样的函数使用有些别扭，不够直观的话。可以自己尝试着重载一下运算符，达到简化的效果。

例如：

    T& operator[] ( Rank r ) const{return _elem[r];}; //重载下标操作符，可以类似于数组形式引用各元素
    myVector<T> & operator= ( myVector<T> const& ); //重载赋值操作符，以便直接克隆向量

像这样重载运算符之后就可已将V.add(0,V.get(1))等这么复杂的写法改成V[0]+=V[1]这么直观的表达式。

LazyChun

关注

8
点赞
踩
37

收藏

觉得还不错? 一键收藏
4
评论
复制链接

分享到 QQ

分享到新浪微博

扫一扫

专栏目录