数组的定义:
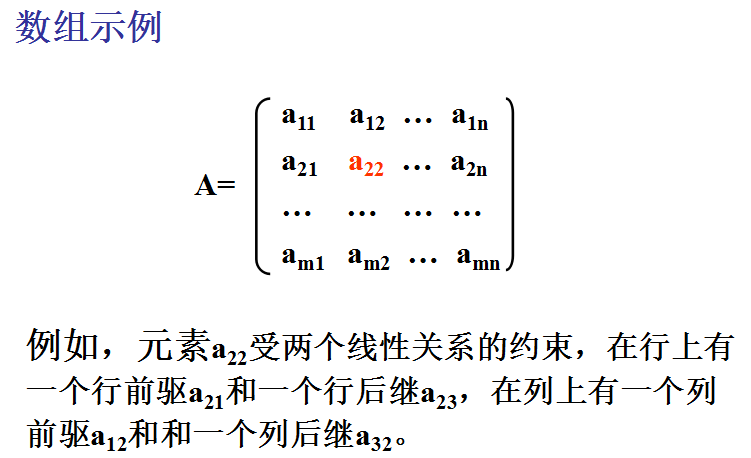
数组是由一组类型相同的数据元素构成的有序集合,每个数据元素称为一个数组元素(简称为元素),每个元素受n(n≥1)个线性关系的约束,每个元素在n个线性关系中的序号i1、i2、…、in称为该元素的下标,并称该数组为 n 维数组。
数组的特点:
元素本身可以具有某种结构,属于同一数据类型; 数组是一个具有固定格式和数量的数据集合。
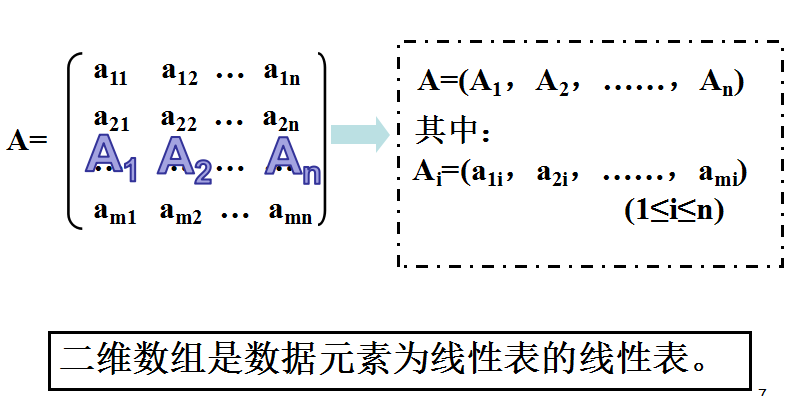
二维数组的定义:
基本操作:
InitArray (&A, n, bound1, ..., boundn)
操作结果:若维数 n 和各维长度合法,则构造相应的数组A,并返回OK。
DestroyArray(&A)
操作结果:销毁数组A。
Value(A, &e, index1, ..., indexn)
初始条件:A是n维数组,e为元素变量,随后是n 个下标值。
操作结果:若各下标不超界,则e赋值为所指定的A的元素值,并返回OK。
Assign(&A, e, index1, ..., indexn)
初始条件:A是n维数组,e为元素变量,随后是n 个下标值。
操作结果:若下标不超界,则将e的值赋给所指定的A的元素,并返回OK。
数组的基本操作:
⑴ 存取:给定一组下标,存储或读出对应的数组元素;
⑵ 修改:给定一组下标,修改与其相对应的数组元素。
存取和修改操作本质上只对应一种操作——寻址
数组一般没有插入和删除操作,所以,一般不用预留空间,适合采用
顺序存储。
数组的顺序表示和实现
类型特点: 1) 只有引用型操作,没有加工型操作; 2) 数组是多维的结构,而存储空间是一个一维的结构。
有两种顺序映象的方式: 1)以行序为主序(低下标优先); 2)以列序为主序(高下标优先);
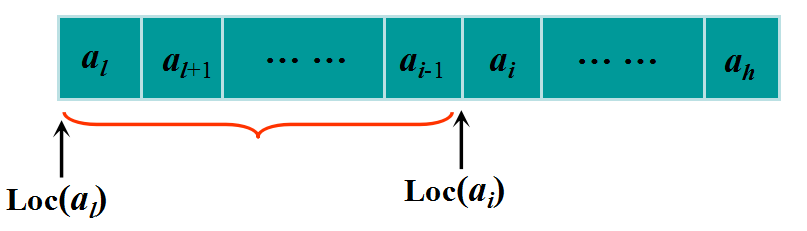
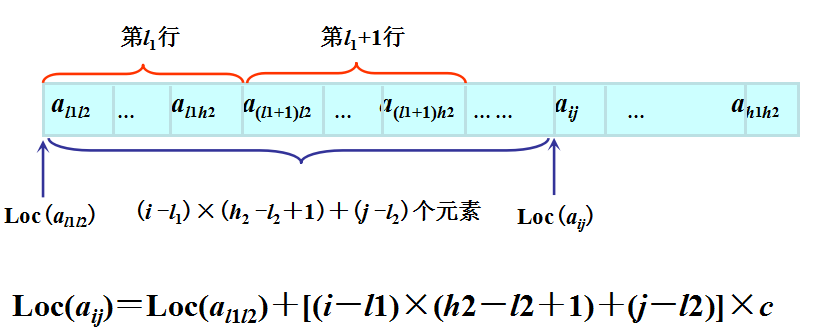
设一维数组的下标的范围为闭区间[l,h],每个数组元素占用 c 个存储单元,则其任一元素 ai 的存储地址可由下式确定: Loc(ai)=Loc(al) + (i-l)×c
数组的顺序表示和实现—二维
常用的映射方法有两种:
按行优先:先行后列,先存储行号较小的元素,行号相同者先存储列号较小的元素。
按列优先:先列后行,先存储列号较小的元素,列号相同者先存储行号较小的元素。
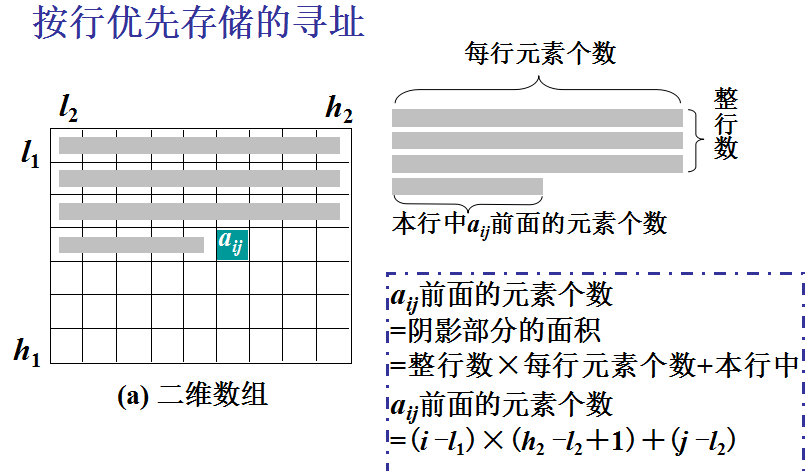
按列优先存储的寻址方法与此类似。
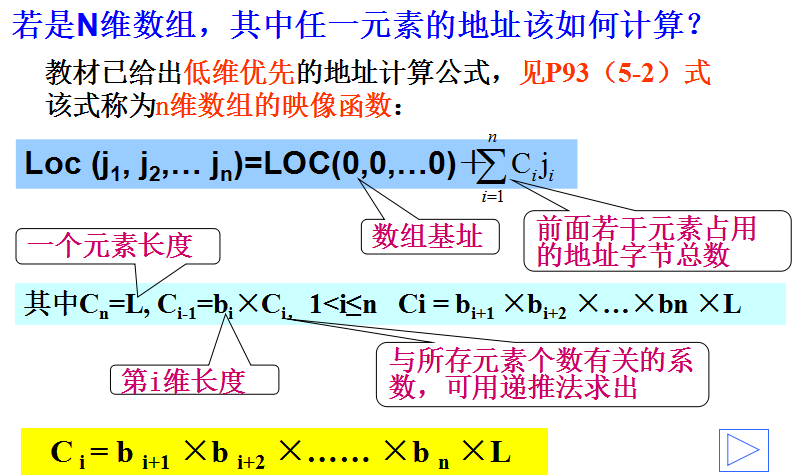
数组的顺序表示和实现—N维
练习:
矩阵的压缩存储
1. 什么是压缩存储?
若多个数据元素的值都相同,则只分配一个元素值的存储空间,且零元素不占存储空间。
2. 什么样的矩阵具备压缩条件?
特殊矩阵(对称矩阵,对角矩阵,三角矩阵) 和稀疏矩阵。
特殊矩阵和稀疏矩阵
特殊矩阵:矩阵中很多值相同的元素并且它们的分布有一定的规律。
稀疏矩阵 : 矩阵中非零元素的个数较少(一般小于5%)
压缩存储的基本思想是:
⑴ 为多个值相同的元素只分配一个存储空间;
⑵ 对零元素不分配存储空间。
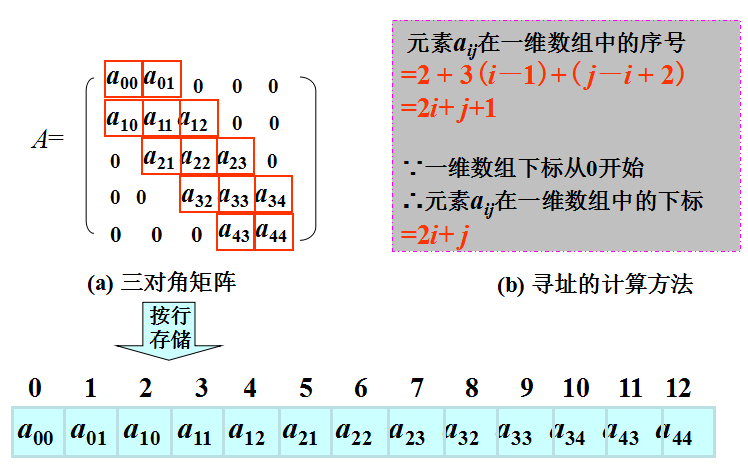
特殊矩阵的压缩存储—对称矩阵
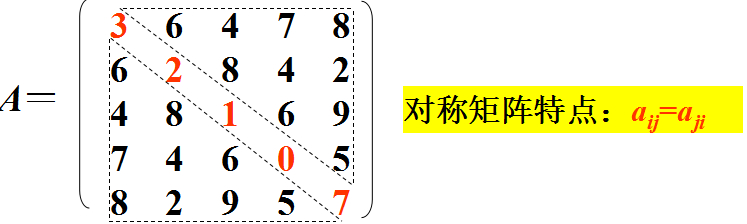
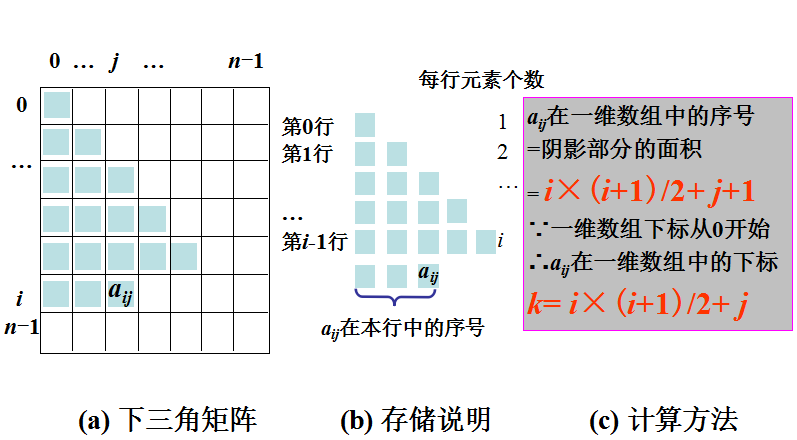
如何压缩存储?
只存储下三角部分的元素。




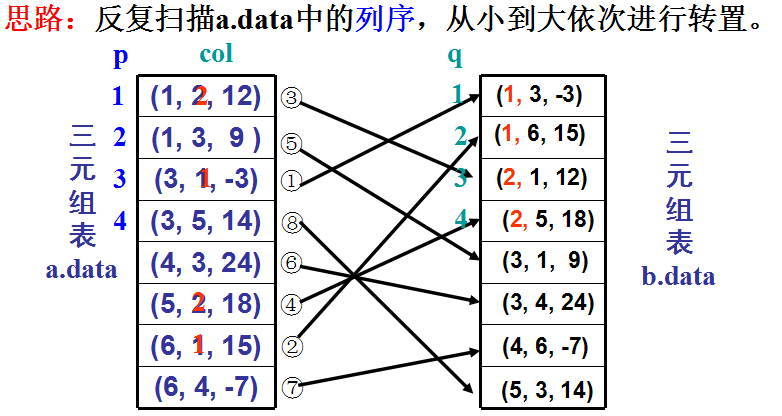
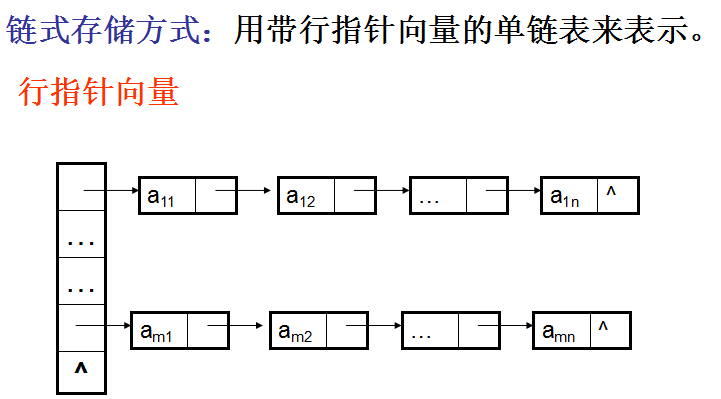
稀疏矩阵的转置操作



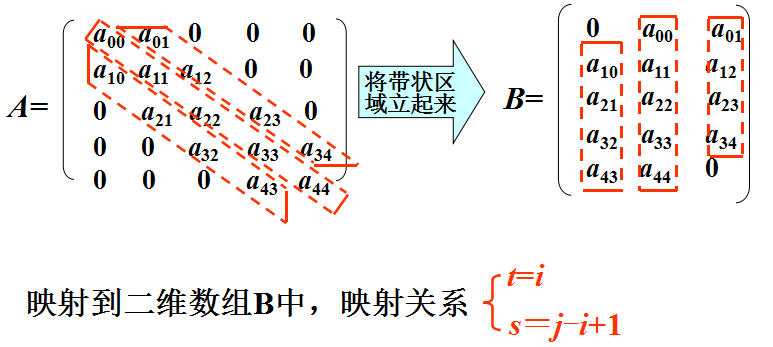
特殊矩阵的压缩存储—对角矩阵
对角矩阵:所有非零元素都集中在以主对角线为中心的带状区域中,除了主对角线和它的上下方若干条对角线的元素外,所有其他元素都为零。



问题:
如果只存储稀疏矩阵中的非零元素,那这些元素的位置信息该如何表示?
解决思路: 对每个非零元素增开若干存储单元,例如存放其所在的行号和列号,便可准确反映该元素所在位置。
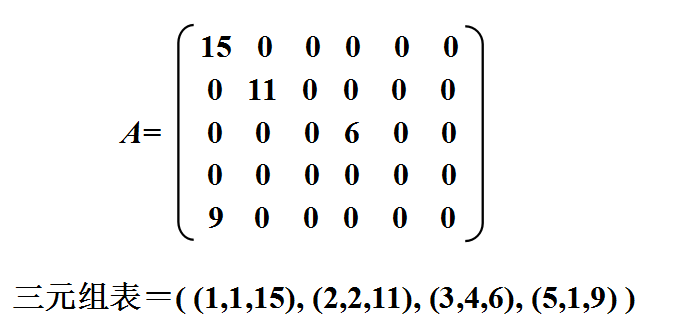
实现方法: 将每个非零元素用一个三元组(i,j,aij)来表示,则每个稀疏矩阵可用一个三元组表来表示。
将稀疏矩阵中的每个非零元素表示为: (行号,列号,非零元素值)——三元组
三元组表:将稀疏矩阵的非零元素对应的三元组所构成的集合,按行优先的顺序排列成一个线性表。


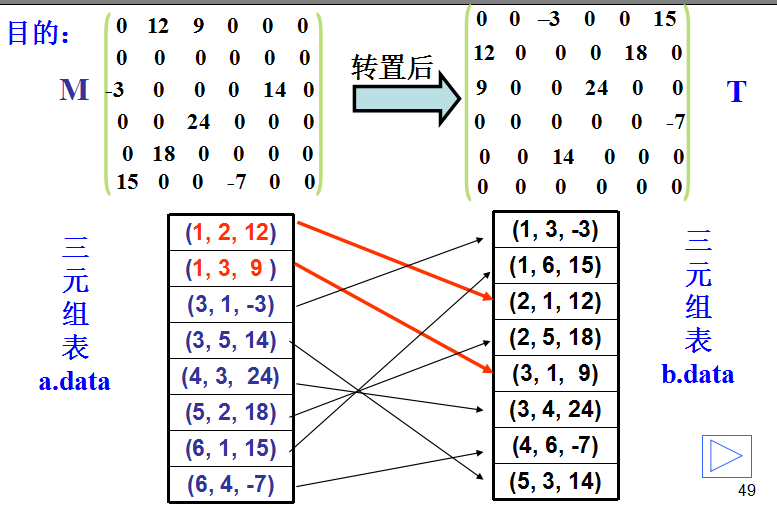
稀疏矩阵的转置操作

(1)每个元素的行下标和列下标互换(即三元组中的i和j互换);
(2)T的总行数mu和总列数nu与M的不同(互换);
(3)重排三元组内元素顺序,使转置后的三元组也按行(或列)为主序有规律的排列。
上述(1)(2)较好实现,那应该如何实现(3)呢
方法Ⅰ 压缩转置
基本思想:
直接取,顺序存。即在A的三元组顺序表中依次找第1列、第2列、…直到最后一列的三元组,并将找到的每个三元组的行、列交换后顺序存储到B的三元组顺序表中。

算法Ⅰ 压缩转置——伪代码
1. 设置转置后矩阵B的行数、列数和非零元个数;
2. 在B中设置初始存储位置pb;
3. for (col=最小列号; col<=最大列号; col++)
3.1 在A中查找列号为col的三元组;
3.2 交换其行号和列号,存入B中pb位置;
3.3 pb++;

算法Ⅱ 快速转置
基本思想:顺序取,直接存。即在A中依次取三元组,交换其行号和列号放到B 中适当位置。
如何确定当前从A中取出的三元组在B中的位置?
分析:A中第1列的第一个非零元素一定存储在B中行下标为1的位置上,该列中其它非零元素应存放在B中后面连续的位置上,那么A中第2列的第一个非零元素在B中的位置便等于A中第1列的第一个非零元素在B中的位置加上A中第1列的非零元素的个数,以此类推。
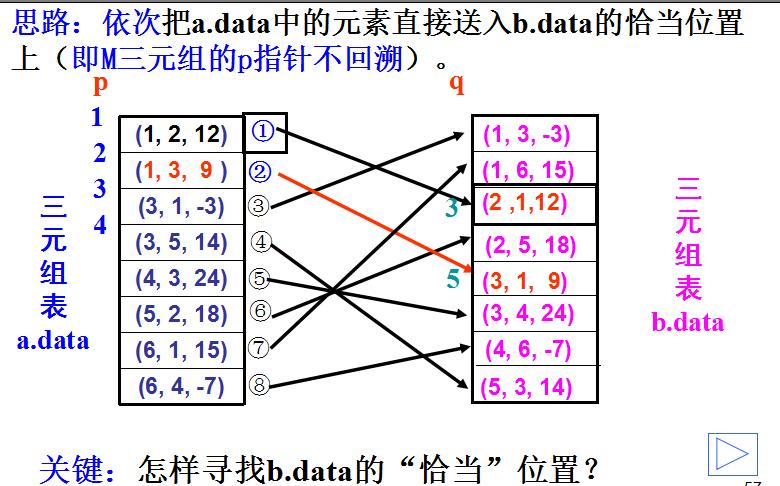
数据结构设计:
引入两个数组作为辅助数据结构:
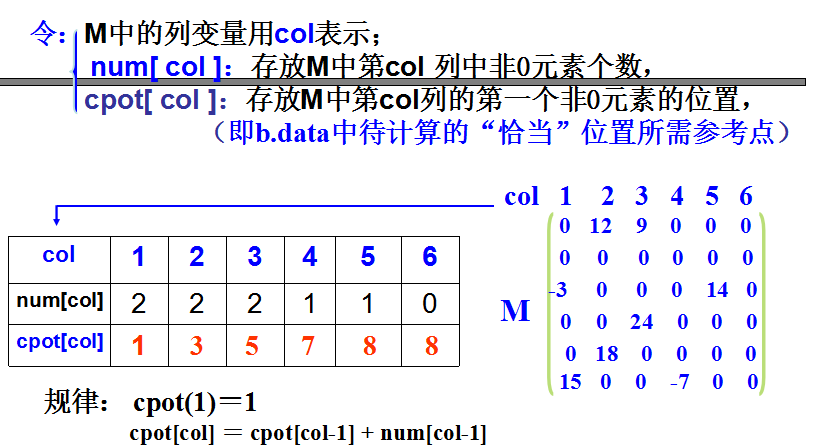
num[nu]:存储矩阵A中某列的非零元素的个数;
cpot[nu]:初值表示矩阵A中某列的第一个非零元素在B中的位置。
设计思路:
如果能预知M矩阵每一列(即T的每一行)的非零元素个数,又能预知第一个非零元素在b.data中的位置,则扫描a.data时便可以将每个元素准确定位(因为已知若干参考点)。
请注意a.data特征:每列首个非零元素必定先被扫描到。
技巧:
利用带辅助向量的三元组表,它正好携带每行(或列)的非零元素个数 NUM(i)以及每行(或列)的第一个非零元素在三元组表中的位置POS(i) 等信息。
快速转置——伪代码:
1. 设置转置后矩阵B的行数、列数和非零元素的个数;
2. 计算A中每一列的非零元素个数;
3. 计算A中每一列的第一个非零元素在B中的下标;
4. 依次取A中的每一个非零元素对应的三元组;
4.1 确定该元素在B中的下标pb;
4.2 将该元素的行号列号交换后存入B中pb的位置;
4.3 预置该元素所在列的下一个元素的存放位置;

快速转置算法的效率分析:
1. 与常规算法相比,附加了生成辅助向量表的工作。增开了2个长度为列长的数组(num[ ]和cpos[ ])。
2. 从时间上,此算法用了4个并列的单循环,而且其中前3个单循环都是用来产生辅助向量表的。
for(col = 1; col <=M.nu; col++) 循环次数=nu;
for( i = 1; i <=M.tu; i ++) 循环次数=tu;
for(col = 2; col <=M.nu; col++) 循环次数=nu;
for( p =1; p <=M.tu ; p ++ ) 循环次数=tu;
该算法的时间复杂度=(nu*2)+(tu*2)=O (nu+tu)
讨论:最恶劣情况是tu=nu*mu(即矩阵中全部是非零元素), 而此时的时间复杂度也只是O(mu*nu),并未超过传统转置算法的时间复杂度。
































 1520
1520

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








