强化学习基础-动态规划

回顾 上一篇关于联立贝尔曼方程求解状态价值函数：

不过这种显式地列出联立方程并直接求解的方法只对小问题有效。在实践中，当状态和行动模式的数量稍有增加，这种方法就会变得难以使用(需要联立很多方程)。对于这样的情况，应运而生了一种方法动态规划法（dynamic programming, DP）。即使状态和行动的数量增加到一定程度，通过动态规划法，也可以对价值函数进行评估。本章将介绍动态规划法。

而调整方法常常是迭代优化。

当然，强化学习的最终目标是策略控制。但要实现这一目标，首先要解决的常常是策略评估。这是因为在大部分情况下，我们很难直接获得最优策略。

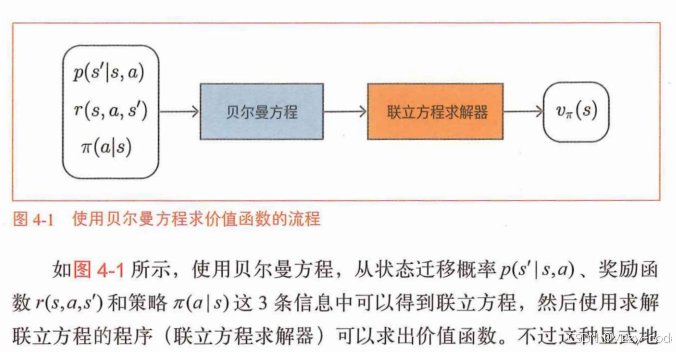
1.动态规划法(DP)进行策略评估

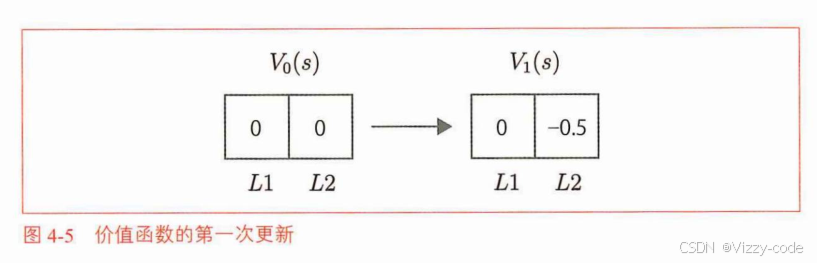
用第k次的状态价值函数：输入s_t+1-返回价值， 更新第（k+1）次迭代的状态价值函数：输入s_t-返回价值

例如在之前的使用随机性策略的问题情景中，对这个策略（智能代理或以0.5的概率向左移
动，或以0.5的概率向右移动，来采取行动。）进行评估：

问题情景回顾：

这个问题中的状态迁移是确定性的。也就是说，如果在状态s下执行了行动a，那么下一个状态就只有一个，公式简化：

迭代一次：

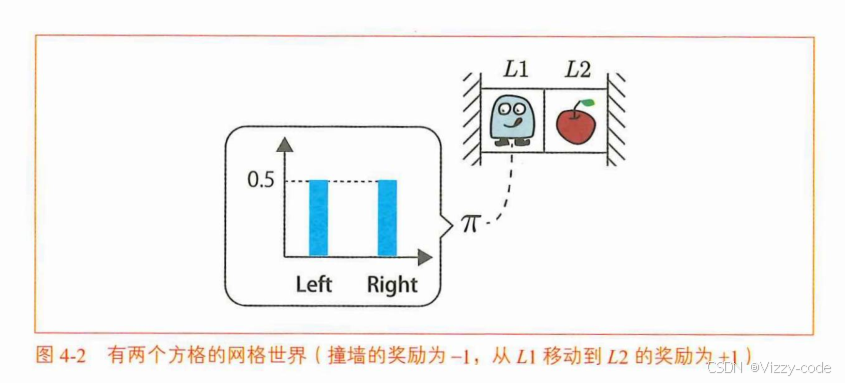
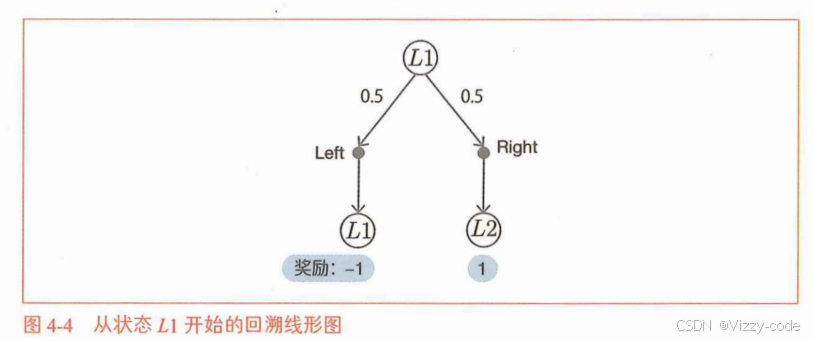
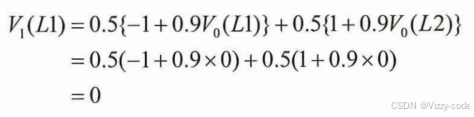
2.解决更大的问题（多个状态）

如果使用迭代策略评估算法，那么即使状态和行动模式的数量大一些，也能髙效求解。本节将从两个方格的网格世界问题“毕业”，开始挑战一个更大的问题（尽管仍然是小问题）。这次我们要处理的是“3x4网格世界”，如图4-8所示。

算法的角度解决这个问题需要准备智能体类和环境类，以及这两个类的互动

对环境类的要求：实现状态迁移与奖励函数

对智能体的要求：使用最优秀策略获得最大收益

对互动的要求：不断进行策略评估，迭代策略，找到最优策略

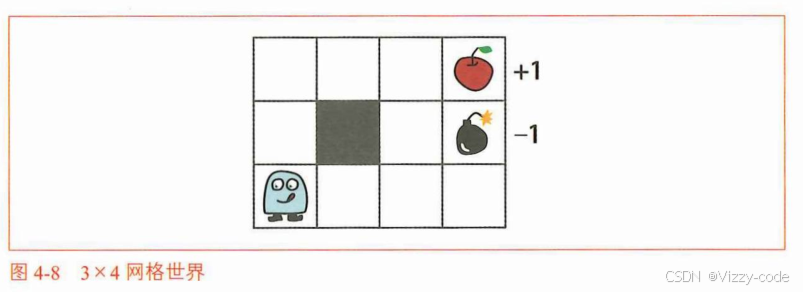
GridWorld 作为环境类，设计了一个 3x4 网格世界环境，包含奖励地图（目标状态奖励 1.0 位于 （0,3），惩罚状态 -1.0 位于 （1,3），位于墙（1,1），其他为 0）、4 个动作（上、下、左、右）和起始状态 （2,0），通过 next_state（状态迁移）、reward（提供奖励）、reset()是将游戏返回到初始状态的方法，具体来说是将智能代理返回到起始位置step(action)方法可以使智能代理执行action行动，并将时间前进一步。这两个方法实际上是被用来移动智能代理。迭代策略评估算法不使用这两个方法，因为它并不使智能代理实际采取行动。render_v 方法则利用 matplotlib 生成热力图（RdYlGn 颜色映射，负值红深、正值绿深）并显示状态价值或特殊标签（如 “Wall”、“R 1.0 （GOAL）”），原点 （0,0） 位于左上角。

import numpy as np
import matplotlib.pyplot as plt


class GridWorld:
    def __init__(self):
        """初始化GridWorld环境"""
        self.action_space = [0, 1, 2, 3]  # 动作空间：0=UP, 1=DOWN, 2=LEFT, 3=RIGHT
        self.action_meaning = {
            0: "UP",
            1: "DOWN",
            2: "LEFT",
            3: "RIGHT",
        }
        # 奖励地图，None表示墙，1.0表示目标状态，-1.0表示惩罚状态
        self.reward_map = np.array([
            [0, 0, 0, 1.0],  # R 1.0 (GOAL)
            [0, None, 0, -1.0],  # R -1.0
            [0, 0, 0, 0]
        ])
        self.goal_state = (0, 3)  # 目标状态
        self.wall_state = (1, 1)  # 墙的状态
        self.start_state = (2, 0)  # 起始状态
        self.agent_state = self.start_state  # 智能代理当前状态

    @property
    def height(self):
        """返回网格的高度"""
        return len(self.reward_map)

    @property
    def width(self):
        """返回网格的宽度"""
        return len(self.reward_map[0])

    @property
    def shape(self):
        """返回网格的形状"""
        return self.reward_map.shape

    def actions(self):
        """返回所有可能的动作"""
        return self.action_space  # [0, 1, 2, 3]

    def states(self):
        """生成所有可能的 states"""
        for h in range(self.height):
            for w in range(self.width):
                yield (h, w)

    def next_state(self, state, action):
        """计算下一步状态"""
        action_move_map = [(-1, 0), (1, 0), (0, -1), (0, 1)]  # 动作对应的移动方向
        move = action_move_map[action]
        next_state = (state[0] + move[0], state[1] + move[1])
        ny, nx = next_state
        # 检查是否超出边界或撞到墙
        if nx < 0 or nx >= self.width or ny < 0 or ny >= self.height:
            next_state = state
        elif next_state == self.wall_state:
            next_state = state
        return next_state  # 返回下一个状态

    def reward(self, state, action, next_state):
        """根据下一个状态返回奖励"""
        return self.reward_map[next_state]

    def reset(self):
        """重置智能代理到起始位置"""
        self.agent_state = self.start_state
        return self.agent_state

    def step(self, action):
        """执行动作并更新状态"""
        next_state = self.next_state(self.agent_state, action)
        reward = self.reward(self.agent_state, action, next_state)
        self.agent_state = next_state
        return next_state, reward

    def render_v(self, v=None, policy=None):
        """渲染网格世界，显示价值函数和热力图效果
        参数:
            v (dict): 状态价值函数，键为状态坐标，值为价值
            policy (dict): 策略，键为状态，值为动作
        """
        # 初始化价值数组，如果v未提供，则用0填充
        value_map = np.zeros(self.shape)
        if v is not None:
            for state in self.states():
                value_map[state] = v.get(state, 0)

        # 创建热力图颜色映射
        plt.figure(figsize=(self.width, self.height))
        plt.imshow(value_map, cmap='RdYlGn', interpolation='nearest', vmin=-1.5, vmax=1.5)

        # 添加价值函数文本
        for (i, j), val in np.ndenumerate(value_map):
            if self.reward_map[i, j] is None:  # 墙
                plt.text(j, i, 'Wall', ha='center', va='center', color='black', fontsize=12, weight='bold')
            elif (i, j) == self.goal_state:  # 目标
                plt.text(j, i, f'R 1.0 (GOAL)', ha='center', va='center', color='black', fontsize=12)
            elif (i, j) == (1, 3):  # 惩罚状态
                plt.text(j, i, 'R -1.0', ha='center', va='center', color='black', fontsize=12)
            else:
                plt.text(j, i, f'{val:.2f}', ha='center', va='center', color='black' if abs(val) < 1 else 'white',
                         fontsize=12)

        # 设置坐标轴
        plt.xticks([])
        plt.yticks([])
        plt.title('3 x 4 网格世界的可视化 (给定状态价值函数值)')
        # 移除 invert_yaxis，确保 (0,0) 在左上角，与图片一致
        plt.show()


# 示例用法
if __name__ == "__main__":
    env = GridWorld()
    # 随机的价值函数
    V = {
        (0, 0): -0.88, (0, 1): -1.17, (0, 2): -0.86, (0, 3): 0.26,
        (1, 0): -0.58, (1, 1): 0, (1, 2): 0.14, (1, 3): 0.21,
        (2, 0): 0.63, (2, 1): 0.10, (2, 2): -0.74, (2, 3): 0.22
    }
    # 渲染
    env.render_v(V)

迭代策略评估的实现（互动）

首先实现只进行一个时间步的更新的方法。这里实现的eval_onestep函数接收以下4个参数。

•  pi (defaultdict) : 策略

• V (defaultdict) : 价值函数

• env (GridWorld) : 环境（动作/状态/下一状态）

• gamma (float) : 折现率

def eval_onestep(pi, V, env, gamma=0.9):
    """单步价值函数更新
    参数:
        pi (dict): 策略，键为状态，值为动作概率字典
        V (dict): 状态价值函数，键为状态，值为价值
        env: GridWorld 环境对象
        gamma (float): 折扣因子，默认 0.9
    返回:
        V (dict): 更新后的状态价值函数
    """
    for state in env.states():  # ①访问各个状态
        if state == env.goal_state:  # ②目的地的价值函数总是为0-终止状态的未来累积奖励为 0
            V[state] = 0
            continue
        action_probs = pi[state]  # probs 是 probabilities 的缩写
        new_V = 0
        # ③访问各行动
        for action, action_prob in action_probs.items():
            next_state = env.next_state(state, action)
            r = env.reward(state, action, next_state)
            # ④新的价值函数
            new_V += action_prob * (r + gamma * V[next_state])
        V[state] = new_V
    return V


# 主程序
if __name__ == "__main__":
    # 初始化环境
    env = GridWorld()

    # 定义均匀随机策略
    pi = {}
    for state in env.states():
        pi[state] = {0: 0.25, 1: 0.25, 2: 0.25, 3: 0.25}  # 每个动作概率为 0.25

    # 初始化价值函数 (全为0)
    V = {state: 0.0 for state in env.states()}

    # 进行一次价值函数更新
    V = eval_onestep(pi, V, env, gamma=0.9)

    # 显示热力图
    env.render_v(V)

代码运行的更新一次的价值函数：

使用参数threshold作为更新的阈值。重复调用eval_onestep函数，当更新量的最大值小于阈值时，停止更新。接下来使用GridWorld类和已经实现的policy_eval函数来进行策略的评估。代码如下所示。

from collections import defaultdict

import numpy as np
import matplotlib.pyplot as plt


class GridWorld:
    def __init__(self):
        """初始化GridWorld环境"""
        self.action_space = [0, 1, 2, 3]  # 动作空间：0=UP, 1=DOWN, 2=LEFT, 3=RIGHT
        self.action_meaning = {
            0: "UP",
            1: "DOWN",
            2: "LEFT",
            3: "RIGHT",
        }
        # 奖励地图，None表示墙，1.0表示目标状态，-1.0表示惩罚状态
        self.reward_map = np.array([
            [0, 0, 0, 1.0],  # R 1.0 (GOAL)
            [0, None, 0, -1.0],  # R -1.0
            [0, 0, 0, 0]
        ])
        self.goal_state = (0, 3)  # 目标状态
        self.wall_state = (1, 1)  # 墙的状态
        self.start_state = (2, 0)  # 起始状态
        self.agent_state = self.start_state  # 智能代理当前状态

    @property
    def height(self):
        """返回网格的高度"""
        return len(self.reward_map)

    @property
    def width(self):
        """返回网格的宽度"""
        return len(self.reward_map[0])

    @property
    def shape(self):
        """返回网格的形状"""
        return self.reward_map.shape

    def actions(self):
        """返回所有可能的动作"""
        return self.action_space  # [0, 1, 2, 3]

    def states(self):
        """生成所有可能的 states"""
        for h in range(self.height):
            for w in range(self.width):
                yield (h, w)

    def next_state(self, state, action):
        """计算下一步状态"""
        action_move_map = [(-1, 0), (1, 0), (0, -1), (0, 1)]  # 动作对应的移动方向
        move = action_move_map[action]
        next_state = (state[0] + move[0], state[1] + move[1])
        ny, nx = next_state
        # 检查是否超出边界或撞到墙
        if nx < 0 or nx >= self.width or ny < 0 or ny >= self.height:
            next_state = state
        elif next_state == self.wall_state:
            next_state = state
        return next_state  # 返回下一个状态

    def reward(self, state, action, next_state):
        """根据下一个状态返回奖励"""
        return self.reward_map[next_state]

    def reset(self):
        """重置智能代理到起始位置"""
        self.agent_state = self.start_state
        return self.agent_state

    def step(self, action):
        """执行动作并更新状态"""
        next_state = self.next_state(self.agent_state, action)
        reward = self.reward(self.agent_state, action, next_state)
        self.agent_state = next_state
        return next_state, reward

    def render_v(self, v=None, policy=None):
        """渲染网格世界，显示价值函数和热力图效果
        参数:
            v (dict): 状态价值函数，键为状态坐标，值为价值
            policy (dict): 策略，键为状态，值为动作
        """
        # 初始化价值数组，如果v未提供，则用0填充
        value_map = np.zeros(self.shape)
        if v is not None:
            for state in self.states():
                value_map[state] = v.get(state, 0)

        # 创建热力图颜色映射
        plt.figure(figsize=(self.width, self.height))
        plt.imshow(value_map, cmap='RdYlGn', interpolation='nearest', vmin=-1.5, vmax=1.5)

        # 添加价值函数文本
        for (i, j), val in np.ndenumerate(value_map):

                plt.text(j, i, f'{val:.2f}', ha='center', va='center', color='black' if abs(val) < 1 else 'white',
                         fontsize=12)

        # 设置坐标轴
        plt.xticks([])
        plt.yticks([])
        plt.title('3 x 4 网格世界的可视化 (给定状态价值函数值)')
        plt.show()


def eval_onestep(pi, V, env, gamma=0.9):
    """单步价值函数更新
    参数:
        pi (dict): 策略，键为状态，值为动作概率字典
        V (dict): 状态价值函数，键为状态，值为价值
        env: GridWorld 环境对象
        gamma (float): 折扣因子，默认 0.9
    返回:
        V (dict): 更新后的状态价值函数
    """
    for state in env.states():  # ①访问各个状态
        if state == env.goal_state:  # ②目的地的价值函数总是为0
            V[state] = 0
            continue
        action_probs = pi[state]  # probs 是 probabilities 的缩写
        new_V = 0
        # ③访问各行动
        for action, action_prob in action_probs.items():
            next_state = env.next_state(state, action)
            r = env.reward(state, action, next_state)
            # ④新的价值函数
            new_V += action_prob * (r + gamma * V[next_state])
        V[state] = new_V
    return V


def policy_eval(pi, V, env, gamma, threshold=0.001):
    """策略评估直到收敛
    参数:
        pi (dict): 策略，键为状态，值为动作概率字典
        V (dict): 状态价值函数，键为状态，值为价值
        env: GridWorld 环境对象
        gamma (float): 折扣因子
        threshold (float): 收敛阈值，默认 0.001
    返回:
        V (dict): 收敛后的状态价值函数
    """
    while True:
        old_V = V.copy()  # 更新前的价值函数
        V = eval_onestep(pi, V, env, gamma)
        # 求更新量的最大值
        delta = 0
        for state in V.keys():
            t = abs(V[state] - old_V[state])
            if delta < t:
                delta = t
        # 与阈值比较
        if delta < threshold:
            break
    return V


# 主程序
if __name__ == "__main__":
    # 初始化环境
    env = GridWorld()

    # 定义均匀随机策略
    pi = defaultdict(lambda :{0: 0.25, 1: 0.25, 2: 0.25, 3: 0.25})
    # 初始化价值函数 (全为0)
    V = defaultdict( lambda: 0)
    '''  
    pi = {}
    for state in env.states():
        pi[state] = {0: 0.25, 1: 0.25, 2: 0.25, 3: 0.25}  # 每个动作概率为 0.25

    # 初始化价值函数 (全为0)
    V = {state: 0.0 for state in env.states()}
    '''
    # 进行策略评估直到收敛
    V = policy_eval(pi, V, env, gamma=0.9, threshold=0.001)

    # 显示热力图
    env.render_v(V)

为什么一定收敛？
• 有限空间：只有 12 个格子，信息传完就没新东西了。
• 折扣 𝛾<1：像刹车，防止价值无限涨。
• 规则清晰：每次更新用同一个公式（贝尔曼方程）

运行结果：

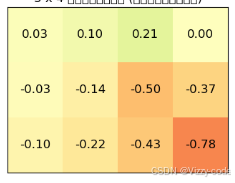
显示了随机性策略的价值函数。例如，左下角的起点的价值函数是-0.10。这意味着如果智能代理从左下角的起点随机移动，那么获得的收益的期望值将是-0.10。智能代理也可能因为随机移动而意外地得到炸弹。根据-0.10可知，得到炸弹（-1的奖励）的概率比得到苹果（+1的奖励）的概率略大一些。另外，总的来说，底部和中间的几行都是负数。这说明炸弹在这些地方的影响更大。

3.策略迭代法得到最优策略

在上节中，我们使用DP评估了策略。那是一种叫作“迭代策略评估”的算法。除了可以对策略进行评估，还可以对策略进行改进。本节将学习改进策略的方法。

首先引入如下符号：

我们在 4.2 节中已经实现了评

估状态价值函数的算法 。 现在我们有了找出最优策略的关键思路 。 该方法

如图 4-14 所示

比较V1和V0，看V1是否>V0

是：更新策略

否：达到最佳策略

也就是：初始化策略，评估策略得到V0，用V0贪婪化更新策略

如果将此过程持续下去 ， 那么就会达到策略

不再因贪婪化而变更的一个点 。 此时的策略就是最优策略 。 这种重复评估 和 改进的算法叫作策略迭代法

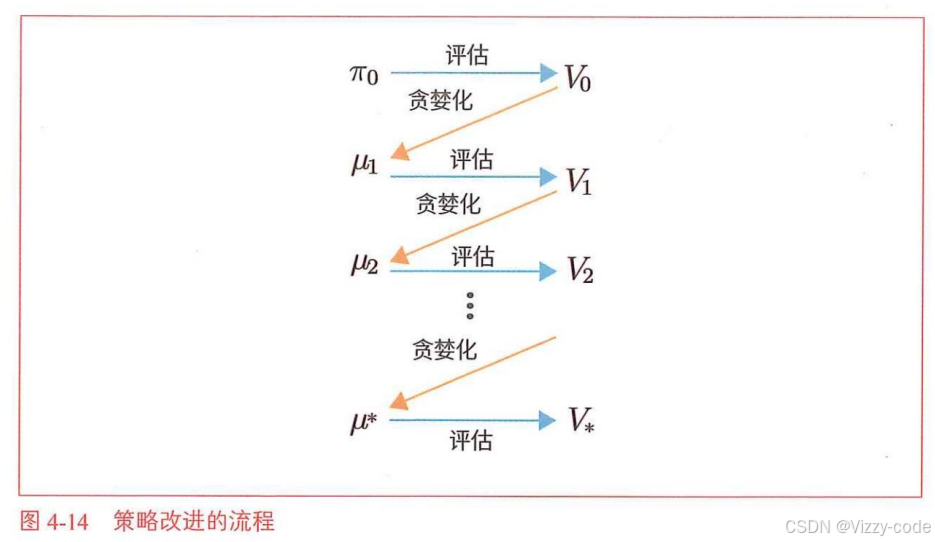
用价值函数贪婪化更新策略

基于行动价值函数的贝尔曼最优方程：目的是根据当前状态的价值函数，选择使得最大的参数a，获得确定性的策略（在该状态下100%选择什么行动）

代码（对所有的状态，遍历所有行动，记录所有行动带来的价值，选出该状态下价值最大的行动）：

import numpy as np
import matplotlib.pyplot as plt

class GridWorld:
    def __init__(self):
        """初始化GridWorld环境"""
        self.action_space = [0, 1, 2, 3]  # 动作空间：0=UP, 1=DOWN, 2=LEFT, 3=RIGHT
        self.action_meaning = {
            0: "UP",
            1: "DOWN",
            2: "LEFT",
            3: "RIGHT",
        }
        # 奖励地图，None表示墙，1.0表示目标状态，-1.0表示惩罚状态
        self.reward_map = np.array([
            [0, 0, 0, 1.0],  # R 1.0 (GOAL)
            [0, None, 0, -1.0],  # R -1.0
            [0, 0, 0, 0]
        ])
        self.goal_state = (0, 3)  # 目标状态
        self.wall_state = (1, 1)  # 墙的状态
        self.start_state = (2, 0)  # 起始状态
        self.agent_state = self.start_state  # 智能代理当前状态

    @property
    def height(self):
        """返回网格的高度"""
        return len(self.reward_map)

    @property
    def width(self):
        """返回网格的宽度"""
        return len(self.reward_map[0])

    @property
    def shape(self):
        """返回网格的形状"""
        return self.reward_map.shape

    def actions(self):
        """返回所有可能的动作"""
        return self.action_space  # [0, 1, 2, 3]

    def states(self):
        """生成所有可能的 states"""
        for h in range(self.height):
            for w in range(self.width):
                yield (h, w)

    def next_state(self, state, action):
        """计算下一步状态"""
        action_move_map = [(-1, 0), (1, 0), (0, -1), (0, 1)]  # 动作对应的移动方向
        move = action_move_map[action]
        next_state = (state[0] + move[0], state[1] + move[1])
        ny, nx = next_state
        # 检查是否超出边界或撞到墙
        if nx < 0 or nx >= self.width or ny < 0 or ny >= self.height:
            next_state = state
        elif next_state == self.wall_state:
            next_state = state
        return next_state  # 返回下一个状态

    def reward(self, state, action, next_state):
        """根据下一个状态返回奖励"""
        return self.reward_map[next_state]

    def reset(self):
        """重置智能代理到起始位置"""
        self.agent_state = self.start_state
        return self.agent_state

    def step(self, action):
        """执行动作并更新状态"""
        next_state = self.next_state(self.agent_state, action)
        reward = self.reward(self.agent_state, action, next_state)
        self.agent_state = next_state
        return next_state, reward

    def render_v(self, v=None, policy=None):
        """渲染网格世界，显示价值函数和热力图效果
        参数:
            v (dict): 状态价值函数，键为状态坐标，值为价值
            policy (dict): 策略，键为状态，值为动作
        """
        value_map = np.zeros(self.shape)
        if v is not None:
            for state in self.states():
                value_map[state] = v.get(state, 0)

        plt.figure(figsize=(self.width, self.height))
        plt.imshow(value_map, cmap='RdYlGn', interpolation='nearest', vmin=-1.5, vmax=1.5)

        for (i, j), val in np.ndenumerate(value_map):
            if self.reward_map[i, j] is None:
                plt.text(j, i, 'Wall', ha='center', va='center', color='black', fontsize=12, weight='bold')
            elif (i, j) == self.goal_state:
                plt.text(j, i, f'R 1.0 (GOAL)', ha='center', va='center', color='black', fontsize=12)
            elif (i, j) == (1, 3):
                plt.text(j, i, 'R -1.0', ha='center', va='center', color='black', fontsize=12)
            else:
                plt.text(j, i, f'{val:.2f}', ha='center', va='center', color='black' if abs(val) < 1 else 'white', fontsize=12)

        plt.xticks([])
        plt.yticks([])
        plt.title('3 x 4 网格世界的可视化 (给定状态价值函数值)')
        plt.show()

def eval_onestep(pi, V, env, gamma=0.9):
    """单步价值函数更新"""
    for state in env.states():
        if state == env.goal_state:
            V[state] = 0
            continue
        action_probs = pi[state]
        new_V = 0
        for action, action_prob in action_probs.items():
            next_state = env.next_state(state, action)
            r = env.reward(state, action, next_state)
            new_V += action_prob * (r + gamma * V[next_state])
        V[state] = new_V
    return V

def policy_eval(pi, V, env, gamma, threshold=0.001):
    """策略评估直到收敛"""
    while True:
        old_V = V.copy()
        V = eval_onestep(pi, V, env, gamma)
        delta = 0
        for state in V.keys():
            t = abs(V[state] - old_V[state])
            if delta < t:
                delta = t
        if delta < threshold:
            break
    return V

def argmax(d):
    """返回字典中值最大的键"""
    max_value = max(d.values())
    max_key = None
    for key, value in d.items():
        if value == max_value:
            max_key = key
            break  # 取第一个最大值对应的键
    return max_key

def greedy_policy(V, env, gamma):
    """基于当前价值函数生成贪心策略
    参数:
        V (dict): 状态价值函数，键为状态，值为价值
        env: GridWorld 环境对象
        gamma (float): 折扣因子
    返回:
        pi (dict): 贪心策略，键为状态，值为动作概率字典
    """
    pi = {}
    
    for state in env.states():
        # 跳过目标状态（终止状态无动作）
        if state == env.goal_state:
            continue
            
        # 计算每个动作的价值
        action_values = {}
        for action in env.actions():
            next_state = env.next_state(state, action)
            r = env.reward(state, action, next_state)
            value = r + gamma * V[next_state]  # ① 计算动作价值：即时奖励 + 折扣后的未来价值
            action_values[action] = value
        
        # 选择价值最大的动作
        max_action = argmax(action_values)  # ② 找到最大动作价值对应的动作
        
        # 构造贪心策略：最大价值动作概率为 1，其余为 0
        action_probs = {0: 0.0, 1: 0.0, 2: 0.0, 3: 0.0}
        action_probs[max_action] = 1.0
        pi[state] = action_probs  # ③ 将策略存储到 pi 中
    
    return pi

# 主程序
if __name__ == "__main__":
    # 初始化环境
    env = GridWorld()

    # 初始化价值函数 (全为0)
    V = {state: 0.0 for state in env.states()}

    # 定义初始均匀随机策略（排除目标状态）
    pi = {}
    for state in env.states():
        if state != env.goal_state:
            pi[state] = {0: 0.25, 1: 0.25, 2: 0.25, 3: 0.25}

    # 第一次策略评估
    V = policy_eval(pi, V, env, gamma=0.9, threshold=0.001)
    print("第一次策略评估后的价值函数:")
    env.render_v(V)

    # 使用贪心策略改进
    pi = greedy_policy(V, env, gamma=0.9)
    print("贪心策略改进后的策略:", pi)

    # 第二次策略评估
    V = policy_eval(pi, V, env, gamma=0.9, threshold=0.001)
    print("第二次策略评估后的价值函数:")
    env.render_v(V)

import numpy as np
import matplotlib.pyplot as plt

class GridWorld:
    def __init__(self):
        """初始化GridWorld环境"""
        self.action_space = [0, 1, 2, 3]  # 动作空间：0=UP, 1=DOWN, 2=LEFT, 3=RIGHT
        self.action_meaning = {
            0: "UP",
            1: "DOWN",
            2: "LEFT",
            3: "RIGHT",
        }
        # 奖励地图，None表示墙，1.0表示目标状态，-1.0表示惩罚状态
        self.reward_map = np.array([
            [0, 0, 0, 1.0],  # R 1.0 (GOAL)
            [0, None, 0, -1.0],  # R -1.0
            [0, 0, 0, 0]
        ])
        self.goal_state = (0, 3)  # 目标状态
        self.wall_state = (1, 1)  # 墙的状态
        self.start_state = (2, 0)  # 起始状态
        self.agent_state = self.start_state  # 智能代理当前状态

    @property
    def height(self):
        """返回网格的高度"""
        return len(self.reward_map)

    @property
    def width(self):
        """返回网格的宽度"""
        return len(self.reward_map[0])

    @property
    def shape(self):
        """返回网格的形状"""
        return self.reward_map.shape

    def actions(self):
        """返回所有可能的动作"""
        return self.action_space  # [0, 1, 2, 3]

    def states(self):
        """生成所有可能的 states"""
        for h in range(self.height):
            for w in range(self.width):
                yield (h, w)

    def next_state(self, state, action):
        """计算下一步状态"""
        action_move_map = [(-1, 0), (1, 0), (0, -1), (0, 1)]  # 动作对应的移动方向
        move = action_move_map[action]
        next_state = (state[0] + move[0], state[1] + move[1])
        ny, nx = next_state
        if nx < 0 or nx >= self.width or ny < 0 or ny >= self.height:
            next_state = state
        elif next_state == self.wall_state:
            next_state = state
        return next_state  # 返回下一个状态

    def reward(self, state, action, next_state):
        """根据下一个状态返回奖励"""
        return self.reward_map[next_state]

    def reset(self):
        """重置智能代理到起始位置"""
        self.agent_state = self.start_state
        return self.agent_state

    def step(self, action):
        """执行动作并更新状态"""
        next_state = self.next_state(self.agent_state, action)
        reward = self.reward(self.agent_state, action, next_state)
        self.agent_state = next_state
        return next_state, reward

    def render_v(self, v=None, policy=None):
        """渲染网格世界，显示价值函数和热力图效果"""
        value_map = np.zeros(self.shape)
        if v is not None:
            for state in self.states():
                value_map[state] = v.get(state, 0)

        plt.figure(figsize=(self.width, self.height))
        plt.imshow(value_map, cmap='RdYlGn', interpolation='nearest', vmin=-1.5, vmax=1.5)

        for (i, j), val in np.ndenumerate(value_map):
            if self.reward_map[i, j] is None:
                plt.text(j, i, 'Wall', ha='center', va='center', color='black', fontsize=12, weight='bold')
            elif (i, j) == self.goal_state:
                plt.text(j, i, f'R 1.0 (GOAL)', ha='center', va='center', color='black', fontsize=12)
            elif (i, j) == (1, 3):
                plt.text(j, i, 'R -1.0', ha='center', va='center', color='black', fontsize=12)
            else:
                plt.text(j, i, f'{val:.2f}', ha='center', va='center', color='black' if abs(val) < 1 else 'white', fontsize=12)

        plt.xticks([])
        plt.yticks([])
        plt.title('3 x 4 网格世界的可视化 (给定状态价值函数值)')
        plt.show()

def eval_onestep(pi, V, env, gamma=0.9):
    """单步价值函数更新"""
    for state in env.states():
        if state == env.goal_state:
            V[state] = 0
            continue
        if state not in pi:
            continue
        action_probs = pi[state]
        new_V = 0
        for action, action_prob in action_probs.items():
            next_state = env.next_state(state, action)
            r = env.reward(state, action, next_state)
            new_V += action_prob * (r + gamma * V[next_state])
        V[state] = new_V
    return V

def policy_eval(pi, V, env, gamma, threshold=0.001):
    """策略评估直到收敛"""
    while True:
        old_V = V.copy()
        V = eval_onestep(pi, V, env, gamma)
        delta = 0
        for state in V.keys():
            t = abs(V[state] - old_V[state])
            if delta < t:
                delta = t
        if delta < threshold:
            break
    return V

def argmax(d):
    """返回字典中值最大的键"""
    max_value = max(d.values())
    max_key = None
    for key, value in d.items():
        if value == max_value:
            max_key = key
            break
    return max_key

def greedy_policy(V, env, gamma):
    """基于当前价值函数生成贪心策略"""
    pi = {}
    for state in env.states():
        if state == env.goal_state:
            continue
        action_values = {}
        for action in env.actions():
            next_state = env.next_state(state, action)
            r = env.reward(state, action, next_state)
            value = r + gamma * V[next_state]
            action_values[action] = value
        max_action = argmax(action_values)
        action_probs = {0: 0.0, 1: 0.0, 2: 0.0, 3: 0.0}
        action_probs[max_action] = 1.0
        pi[state] = action_probs
    return pi

def policy_iter(env, gamma, threshold=0.001, is_render=False):
    """策略迭代算法
    参数:
        env: GridWorld 环境对象
        gamma (float): 折扣因子
        threshold (float): 策略评估收敛阈值
        is_render (bool): 是否渲染每次迭代的价值函数
    返回:
        pi (dict): 最终的最优策略
    """
    # 初始化策略（均匀随机策略）和价值函数
    pi = {}
    for state in env.states():
        if state != env.goal_state:
            pi[state] = {0: 0.25, 1: 0.25, 2: 0.25, 3: 0.25}  # 均匀随机策略
    V = {state: 0.0 for state in env.states()}

    while True:
        # 步骤 1：策略评估
        V = policy_eval(pi, V, env, gamma, threshold)  # 评估当前策略的价值函数

        # 步骤 2：策略改进
        new_pi = greedy_policy(V, env, gamma)  # 根据价值函数生成贪心策略

        # 如果需要渲染，显示当前价值函数
        if is_render:
            env.render_v(V, pi)

        # 步骤 3：检查策略是否收敛
        # 比较 new_pi 和 pi 是否相同（排除目标状态）
        is_same = True
        for state in env.states():
            if state == env.goal_state:
                continue
            if state not in pi or state not in new_pi:
                is_same = False
                break
            if pi[state] != new_pi[state]:
                is_same = False
                break

        # 更新策略
        pi = new_pi

        # 如果策略不再变化，退出循环
        if is_same:
            break

    return pi

# 主程序
if __name__ == "__main__":
    # 初始化环境
    env = GridWorld()

    # 运行策略迭代，启用渲染
    pi = policy_iter(env, gamma=0.9, threshold=0.001, is_render=True)

    # 打印最终策略
    print("最终策略:", pi)

    # 最后一次策略评估，显示最终价值函数
    V = {state: 0.0 for state in env.states()}
    V = policy_eval(pi, V, env, gamma=0.9, threshold=0.001)
    print("最终价值函数:")
    env.render_v(V)

结果：

最优策略：

最终策略: {(0, 0): {0: 0.0, 1: 0.0, 2: 0.0, 3: 1.0}, (0, 1): {0: 0.0, 1: 0.0, 2: 0.0, 3: 1.0}, (0, 2): {0: 0.0, 1: 0.0, 2: 0.0, 3: 1.0}, (1, 0): {0: 1.0, 1: 0.0, 2: 0.0, 3: 0.0}, (1, 1): {0: 1.0, 1: 0.0, 2: 0.0, 3: 0.0}, (1, 2): {0: 1.0, 1: 0.0, 2: 0.0, 3: 0.0}, (1, 3): {0: 1.0, 1: 0.0, 2: 0.0, 3: 0.0}, (2, 0): {0: 1.0, 1: 0.0, 2: 0.0, 3: 0.0}, (2, 1): {0: 0.0, 1: 0.0, 2: 0.0, 3: 1.0}, (2, 2): {0: 1.0, 1: 0.0, 2: 0.0, 3: 0.0}, (2, 3): {0: 0.0, 1: 0.0, 2: 1.0, 3: 0.0}}

进一步优化——值迭代

对每个位置S先改进，再评估（评估时的状态价值函数只更新一次）

下面是推导（对上面的数学原理做了补充-可以不看）“

”

import numpy as np
import matplotlib.pyplot as plt

class GridWorld:
    def __init__(self):
        """初始化GridWorld环境"""
        self.action_space = [0, 1, 2, 3]  # 动作空间：0=UP, 1=DOWN, 2=LEFT, 3=RIGHT
        self.action_meaning = {
            0: "UP",
            1: "DOWN",
            2: "LEFT",
            3: "RIGHT",
        }
        # 奖励地图，None表示墙，1.0表示目标状态，-1.0表示惩罚状态
        self.reward_map = np.array([
            [0, 0, 0, 1.0],  # R 1.0 (GOAL)
            [0, None, 0, -1.0],  # R -1.0
            [0, 0, 0, 0]
        ])
        self.goal_state = (0, 3)  # 目标状态
        self.wall_state = (1, 1)  # 墙的状态
        self.start_state = (2, 0)  # 起始状态
        self.agent_state = self.start_state  # 智能代理当前状态

    @property
    def height(self):
        """返回网格的高度"""
        return len(self.reward_map)

    @property
    def width(self):
        """返回网格的宽度"""
        return len(self.reward_map[0])

    @property
    def shape(self):
        """返回网格的形状"""
        return self.reward_map.shape

    def actions(self):
        """返回所有可能的动作"""
        return self.action_space

    def states(self):
        """生成所有可能的 states"""
        for h in range(self.height):
            for w in range(self.width):
                yield (h, w)

    def next_state(self, state, action):
        """计算下一步状态"""
        action_move_map = [(-1, 0), (1, 0), (0, -1), (0, 1)]
        move = action_move_map[action]
        next_state = (state[0] + move[0], state[1] + move[1])
        ny, nx = next_state
        if nx < 0 or nx >= self.width or ny < 0 or ny >= self.height:
            next_state = state
        elif next_state == self.wall_state:
            next_state = state
        return next_state

    def reward(self, state, action, next_state):
        """根据下一个状态返回奖励"""
        return self.reward_map[next_state]

    def reset(self):
        """重置智能代理到起始位置"""
        self.agent_state = self.start_state
        return self.agent_state

    def step(self, action):
        """执行动作并更新状态"""
        next_state = self.next_state(self.agent_state, action)
        reward = self.reward(self.agent_state, action, next_state)
        self.agent_state = next_state
        return next_state, reward

    def render_v(self, v=None, policy=None):
        """渲染网格世界，显示价值函数和热力图效果"""
        value_map = np.zeros(self.shape)
        if v is not None:
            for state in self.states():
                value_map[state] = v.get(state, 0)

        plt.figure(figsize=(self.width, self.height))
        plt.imshow(value_map, cmap='RdYlGn', interpolation='nearest', vmin=-1.5, vmax=1.5)

        for (i, j), val in np.ndenumerate(value_map):
            if self.reward_map[i, j] is None:
                plt.text(j, i, 'Wall', ha='center', va='center', color='black', fontsize=12, weight='bold')
            elif (i, j) == self.goal_state:
                plt.text(j, i, f'R 1.0 (GOAL)', ha='center', va='center', color='black', fontsize=12)
            elif (i, j) == (1, 3):
                plt.text(j, i, 'R -1.0', ha='center', va='center', color='black', fontsize=12)
            else:
                plt.text(j, i, f'{val:.2f}', ha='center', va='center', color='black' if abs(val) < 1 else 'white', fontsize=12)

        plt.xticks([])
        plt.yticks([])
        plt.title('3 x 4 网格世界的可视化 (给定状态价值函数值)')
        plt.show()

def value_iter(env, gamma, threshold=0.001, is_render=False):
    """值迭代算法
    参数:
        env: GridWorld 环境对象
        gamma (float): 折扣因子
        threshold (float): 收敛阈值
        is_render (bool): 是否渲染每次迭代的价值函数
    返回:
        pi (dict): 最优策略
        V (dict): 最优价值函数
    """
    # 初始化价值函数
    V = {state: 0.0 for state in env.states()}

    # 值迭代
    while True:
        old_V = V.copy()
        delta = 0
        for state in env.states():
            if state == env.goal_state:
                V[state] = 0
                continue

            # 计算每个动作的价值，选择最大值
            max_value = float('-inf')
            for action in env.actions():
                next_state = env.next_state(state, action)
                r = env.reward(state, action, next_state)
                value = r + gamma * old_V[next_state]
                if value > max_value:
                    max_value = value
            V[state] = max_value

            # 计算更新量
            t = abs(V[state] - old_V[state])
            if delta < t:
                delta = t

        # 如果需要渲染，显示当前价值函数
        if is_render:
            env.render_v(V)

        # 检查是否收敛
        if delta < threshold:
            break

    # 提取最优策略
    pi = {}
    for state in env.states():
        if state == env.goal_state:
            continue
        action_values = {}
        for action in env.actions():
            next_state = env.next_state(state, action)
            r = env.reward(state, action, next_state)
            value = r + gamma * V[next_state]
            action_values[action] = value
        max_action = max(action_values, key=action_values.get)
        action_probs = {0: 0.0, 1: 0.0, 2: 0.0, 3: 0.0}
        action_probs[max_action] = 1.0
        pi[state] = action_probs

    return pi, V

# 主程序
if __name__ == "__main__":
    # 初始化环境
    env = GridWorld()

    # 运行值迭代，启用渲染
    pi, V = value_iter(env, gamma=0.9, threshold=0.001, is_render=True)

    # 打印最终策略和价值函数
    print("最优策略:", pi)
    print("最优价值函数:", V)

    # 显示最终价值函数的热力图
    env.render_v(V)

小结

我们学习了如何使用DP来获得最优策略。具体的算法是策略迭代法和价值迭代法。

策略迭代（Policy Iteration）：就像你在一个迷宫里，先假设一个走法（策略），然后反复试着计算“这个走法能拿多少奖励”（价值），直到算得很准，再根据这个结果调整走法（改进策略），然后再算……反复循环，直到走法不再变。
值迭代（Value Iteration）：像直接在迷宫里试着估算每个位置的“幸福指数”（价值），每次都挑最好的方向更新这个指数，直到指数稳定，最后一步决定最优走法。过程更直接，不需要中间反复调整走法。

后一章将进行蒙特卡洛算法的介绍，实现不利用状态的最优策略选择。