复数入门

qwq

数轴

这是数轴（的一部分）：

...  -2  -1  0   1   2  ...
 |   |   |   |   |   |   |
 -------------------------

这也是数轴的一部分：

... 114511 114512 114513 114514 114515 114516 ...
 |    |      |      |      |      |      |     |
 -----------------------------------------------
                            |
               114514.1919810 大概在这里

可见，数轴是无限长的，你可以在上面找到所有的实数，比如 $114514,1919810,114514.1919810$（$114514.1919810$ 在 $114514$ 和 $114515$ 之间，靠近 $114514$）。

平方

等等，小学不是学过平方吗？

回顾一下，$a$ 的平方，就是 $a^2$，其实就是 $a\times a$。

这里有一个知识点：所有实数（小学生可理解为所有的数字）的平方都是非负数。

为什么呢？负负得正，如果没学过，就是：

求 $a^2$：

如果 $a\ge 0$：则两个非负数相乘，不可能是负数（溢出请忽略）。

如果 $a<0$：$a$ 可表示为 $-b$，其中 $b$ 是某个正数，我们不关心是几，知道是个正数就好。$-b$ 就是 $-1\times b$。

$$\begin{array}{rl}& a^2\\ =& (-1\times b{)}^2\\ =& (-1\times b)\times (-1\times b)\\ =& (-1\times -1)\times (b\times b)\\ =& 1\times (b\times b)\\ =& b\times b\\ =& b^2\end{array}$$

显然，由于 $b$ 是个正数，则 $b^2$ 必然是个正数，则 $a^2$ 也必然是个正数（$a^2$ 和 $b^2$ 是一样的嘛）。

平方根

       平方树
         |
         |
         |
        /|\
       / | \
      /  |  \
     /|\/|\/|\
  平方的根（平方根）

开个玩笑。

我们现在有一个 可爱的 非负 数 $a$。

我们对它平方了一下，得到了 $a^2$，记为 $b$。

$b$ 是 $a$ 的平方，那么 $a$ 是 $b$ 的什么呢？

通过观察标题发现，$a$ 是 $b$ 的平方根。

$b$ 是 $a$ 的平方记作 $a=b^2$，$b$ 是 $a$ 的平方根记作 $b=\sqrt{a}$，还可以记作 $b=a^{0.5}$，不过第一种更常用。（注意到 $2\times 0.5=1$，猜测立方根也可以记作 $b=a^{\frac{1}{3}}$，是正确的，但是我们这里不用。）

也就是说，$a=\sqrt{b}$。

我们又知道，$b=a^2$。

所以我们可以知道，$a=\sqrt{a^2}$。

这个规律对于所有的实数都成立。

吗？

No。

观察力强的同学可以发现，你拥有了所有 上面我加粗了一个词，非负。

显然，我们知道，$\cancel{1,145,141,919,810^2=1,311,350,016,506,132,470,436,100}$。

上面一段废除，因为 $1,311,350,016,506,132,470,436,100$ 可能有一丢丢的……大，对于基础薄弱的同学，状态不好时不能在 $10\mathrm{s}$ 内精准计算出来。

显然，我们知道，$4^2=16$。

所以，我们就能知道，$\sqrt{16}=4$。这都是很显然的。

但是，我们还能知道，$(-4{)}^2=(-4)\times (-4)=16$。

所以，我们就能知道，$\sqrt{16}=-4$。

综上，$4=-4$。

我们可以继续推：

$$\begin{array}{rl}4=& -4\\ 1=& -1\\ 2=& 0\\ 0=& 2\\ 0=& 1\\ 0+1+1=& 1+1+1\\ 1+1=& 3\end{array}$$

情况不太妙，是不是？

所以，我们需要从根本上解决这个问题。

$\sqrt{a^2}=a$ 仅仅对于非负数成立（$0$ 也成立）。

$\sqrt{a^2}$ 的真正名称是算术平方根。

而平方根，都有两个答案，它们互为相反数，一个是 $k$ 一个是 $-k$。

note：以下我可能嘴瓢把算术平方根说成平方根，如果没有特殊说明请当成算术平方根。

平方根的乘除性质。

有两条定理：

1. $\sqrt{a}\times \sqrt{b}=\sqrt{ab}$ 根号消失定理
2. $\frac{\sqrt{a}}{\sqrt{b}}=\sqrt{\frac{a}{b}}$ 根号消失定理 $\cancel{\times 2}$

其实它们的原理都很简单：

第一种：首先 $a\times b=ab$，将 $a$ 变为 $\sqrt{a}$，$b$ 变为 $\sqrt{b}$，$ab$ 变为 $\sqrt{ab}$，就可以得到。（但是还是不要乱变为好，稍不小心就会 $1+1=3$。）

第二种：类似，相信读者可以自己证明。

无理数危机

1. • Question：$\sqrt{4}=?$
   • Answer：$2$，显然 $2^2=4$
2. • Question：$\sqrt{2.25}=?$
   • Answer：$1.5$，稍加注意可得 $1.5^2=2.25$
3. • Question：$\sqrt{13,113,500,165.06132470436100}=?$
   • Answer：$114,514.1919810$，与上一题性质一样，Attention is all you need.
4. • Question：$\sqrt{2}=?$
   • Answer：$\sqrt{2}$，政治家的智慧。

最后一个问题，你不是来搞笑的？$\sqrt{2}=\sqrt{2}$。

其实，$\sqrt{2}$ 你还真没办法算出来，你随便给我个小数，甚至分数（别来 $\frac{\sqrt{2}}{1}$ 之类的）我都能告诉你大了还是小了，比如 $1.41421356237309504880168872420$，$1.41421356237309504880168872420^2\approx 1.9999999999999999999999999999726$，所以 $1.41421356237309504880168872420$ 小了。又比如 $1.41421356237309504880168872421^2\approx 2.0000000000000000000000000000009$（不是浮点误差），所以 $1.41421356237309504880168872421$ 大了（虽然平时 $1.414$ 完全够用）。如果你找到了一个有限小数，无限循环小数或分子分母均为整数的数，觉得它就是 $\sqrt{2}$，欢迎来告诉我 ，我可以帮你发论文。

综上，$\sqrt{2}$ 无法被平常的方式所表示，那就让只能它是 $\sqrt{2}$，它在数轴上的位置也很好确定，就在 $1$ 和 $2$ 之间（也在我刚刚说的两个数之间）。

负数？

我们可以发现，任何实数的平方都是非负数。

那么如果出现了 $\sqrt{-114514}$ 之类的数，怎么办呢？

我们发现，怎么找都找不到一个数，它的平方是 $-114514$。并且理论上来说有两个数的平方都是 $114514$！

难不成这是一个像 $\frac{0}{0}$ 一样的，无解问题？（声明一句，这个也不是无解，答案是 $\infty$。）

但是，政治家的智慧是无穷的：

既然我们找不到，那我们不妨定义一个？

于是我们定义 $\sqrt{-1}$ 为 $i$（之所以不定义 $\sqrt{-114514}$ 为 $i$，是因为 $\sqrt{-114514}$ 就是 $\sqrt{114514}\times \sqrt{-1}$）。

这里 $i$ 也叫虚数单位。

note：其实教科书上的定义为 $i^2=-1$，但是这样就有两个满足条件的 $i$ 了，所以我不是很喜欢。当然考试中问 $i$ 的定义不要听我的。

但是，$i$ 究竟是哪种数呢？

答案是：虚数。

与其说 $i$ 是虚数，不如说虚数都是由 $i$ 定义出来的。

所有虚数都可以表示为 $bi$，其中 $b$ 是某个实数，比如 $114514.1919810$。

那么，如果我们让虚数和实数相加，会发生什么呢？会出现 $a+bi$，并且无法化简（除非 $ab=0$），这种数就叫做 复数。

现在知道 实数 的名称由来了吧，和虚数相对的数。

所以，$i$ 在数轴上该如何表示呢？

找不到啊！

于是某人 （我） 就提出了一个天才的想法：

一个数乘上 $-1$ 就相当于把它在数轴上的位置逆时针旋转了 $180^{\circ }$，跑到了另一边。那么显而易见，乘两次 $-1$ 就相当于旋转了两次 $180^{\circ }$，旋转了 $360^{\circ }$，相当于没旋转。

所以显而易见，由于 $i^2=-1$，可得，一个数旋转两次 $i$，就相当于旋转了一次 $-1$（抽象），就是旋转两次乘 $i$ 旋转的角度，相当于旋转一次 $180^{\circ }$。

所以说，旋转两次 $i$，相当于旋转 $180^{\circ }$，显然，乘上 $i$ 所旋转的角度就是 $90^{\circ }$。

我们就这样知道了 $i$ 在数轴的哪里：在数轴的上空。

            |3i
            |2i
            |i
-4 -3 -2 -1 |0 1  2  3  4
------------+------------
            |-i
            |-2i
            |-3i

我们不妨再野蛮一点（不太写的下了！放图片吧）

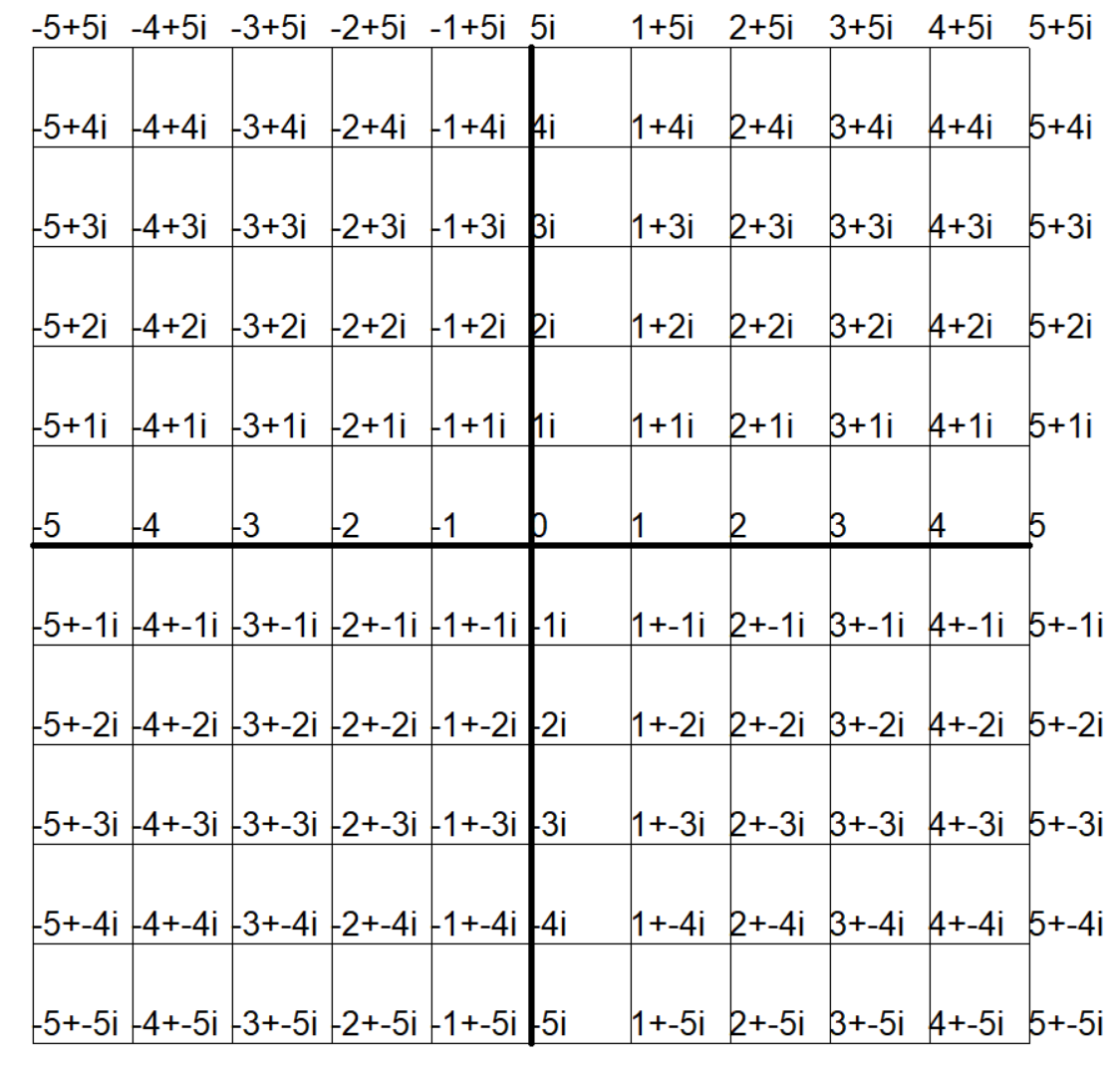
很好理解，$+1$ 相当于往右走一格，$-1$ 相当于往左走一格，$+i$ 相当于往上走一格，$-i$ 相当于往下走一格。

但是这东西，还能叫数轴吗……

称其为 复平面 真是再好不过。既体现出上面有复数，又体现出这是一个平面。

短暂的休息 - 小小地总结

平方，就是一个数乘自己，一个实数的平方永远是非负数。

平方根，就是平方的逆运算。

虚数，就是负数的平方根，表示为 $bi$。

虚数单位，就是 $i=\sqrt{-1}$。

实数，就是没有 $i$ 的数（说了跟没说一样），表示为 $a$。

复数，就是 $\text{实数}+\text{虚数}$，表示为 $a+bi$。

复平面，就是扩充后的数轴，原本数轴上只有实数，现在多了虚数乃至复数。

休息够了吗？${\aleph }_{114514}$ 则运算，启动！！！

复数运算

求模长

一个复数可以看成复平面上的一个点。

而这个复数的模长可以看成这个点到原点（$0$ 点）的距离。

勾股定理可得，一个复数 $a+bi$ 的模长为 $\sqrt{a^2+b^2}$。

求幅角

一个复数不仅可以看做复平面上的一个点，还可以看做复平面上的一个向量（箭头），从原点指向它代表的点。

而幅角就是角度，比如 $-1$ 的角度就是 $180^{\circ }$，$i$ 的角度就是 $90^{\circ }$。

显然，一个向量的幅角就是 $\arctan \frac{b}{a}$。

如果 $a$ 为 $0$，此时看 $b$，如果 $b$ 为正，则幅角位 $90^{\circ }$。如果 $b$ 为负，则幅角为 $-90^{\circ }$。

所以

知道了一个复数的模长和幅角，就可以知道这个复数的值。就像你知道了向哪边走，走多远就可以知道目的地是哪里。

如果模长为 $x$，幅角为 $y$，则复数为：

$$\frac{x}{\cos y}+\frac{x}{\sin y}i$$

加法

众所周知 $(a+bi)+(c+di)=a+bi+c+di=(a+c)+(b+d)i$。

我们来做个练习吧。

$$(1+2i)+(3+4i)=?$$

$$(114+514i)+(1919+810i)=?$$

减法

有什么区别呢？

$$(3+2i)-(4+i)=?$$

$$(114+514i)-(1919+810i)=?$$

乘法

推一推吧~

$$\begin{array}{rl}& (a+bi)\times (c+di)\\ =& ac+adi+bci+bd{i}^2\\ =& ac+(ad+bc)i+(-1)bd\\ =& (ac-bd)+(ad+bc)i\end{array}$$

练习：

$$(1+i)(2-3i)=?$$

$$(2-i)(3-2i)=?$$

$$(5-2i{)}^3=?$$

Attention is all you need.（前方高能警告）

原两个复数的模长分别是：

1. $\sqrt{a^2+b^2}$
2. $\sqrt{c^2+d^2}$

乘积为：
$$\begin{array}{rl}& \sqrt{(a^2+b^2)(c^2+d^2)}\\ =& \sqrt{a^2{c}^2+b^2{d}^2+a^2{d}^2+b^2{c}^2}\end{array}$$

新复数的模长为：
$$\begin{array}{rl}& \sqrt{(ac-bd{)}^2+(ad+bc{)}^2}\\ =& \sqrt{a^2{c}^2+b^2{d}^2-2abcd+a^2{d}^2+b^2{c}^2+2abcd}\\ =& \sqrt{a^2{c}^2+b^2{d}^2+a^2{d}^2+b^2{c}^2}\end{array}$$

两数完全相同。

原两个复数的幅角为：

1. $\arctan \frac{b}{a}$
2. $\arctan \frac{d}{c}$

和为：

$$\begin{array}{rl}& \arctan \frac{b}{a}+\arctan \frac{d}{c}\\ =& \arctan \frac{\frac{b}{a}+\frac{d}{c}}{(1-\frac{bd}{ac})}\\ =& \arctan \frac{\frac{bc+ad}{ac}}{\frac{ac-bd}{ac}}\\ =& \arctan \frac{ad+bc}{ac-bd}\end{array}$$

新向量的幅角为：
$\arctan \frac{ad+bc}{ac-bd}$

两数完全相同。

所以，复数加法遵循着另一个规则：模长相乘，幅角相加。

除法

$$\begin{array}{rl}& \frac{a+bi}{c+di}\\ =& \frac{(a+bi)(c-di)}{(c+di)(c-di)}\\ =& \frac{(ac+bd)+(bc-ad)i}{c^2-(di{)}^2}\\ =& \frac{(ac+bd)+(bc-ad)i}{c^2+d^2}\\ =& \frac{ac+bd}{c^2+d^2}+\frac{bc-ad}{c^2+d^2}i\end{array}$$

看起来有点复杂，我们要验算一下（前方高能警告）：

$$\begin{array}{rl}& (\frac{ac+bd}{c^2+d^2}+\frac{bc-ad}{c^2+d^2}i)(c+di)\\ =& \frac{a{c}^2+bcd}{c^2+d^2}+\frac{acd+b{d}^2}{c^2+d^2}i+\frac{b{c}^2-acd}{c^2+d^2}i-\frac{bcd-a{d}^2}{c^2+d^2}\\ =& \frac{a{c}^2+bcd-bcd+a{d}^2}{c^2+d^2}+\frac{acd+b{d}^2+b{c}^2-acd}{c^2+d^2}i\\ =& \frac{a(c^2+d^2)}{c^2+d^2}+\frac{b(c^2+d^2)}{c^2+d^2}i\\ =& a+bi\end{array}$$

验算完毕。

题不想出了。

平方

自己乘自己，so eazy，不过还是把公式推一推。

$$\begin{array}{rl}& (aa-bb)+(ab+ba)i\\ =& (a^2-b^2)+2abi\end{array}$$
战斗结束。

中场休息

以下默认是 $a+bi$ 或 $a+bi$ 与 $c+di$ 的运算。

模长：$\sqrt{a^2+b^2}$。

幅角：$\{\begin{array}{ll}\arctan \frac{b}{a}& a\ne 0\\ 90^{\circ }& a=0\wedge b>0\\ -90^{\circ }& a=0\wedge b<0\\ 114514^{\circ }& a=0\wedge b=0\end{array}$。

（最后一个开玩笑的，未定义）。

模长为 $x$，幅角为 $y$，则复数为：$ \dfrac{x}{\cos y}+\dfrac{x}{\sin y}i $

加法：$(a+c)+(b+d)i$。

减法：$(a-c)+(b-d)i$。

乘法：$(ac-bd)+(ad+bc)i$ 且模长相乘，幅角相加。

除法：$\frac{ac+bd}{c^2+d^2}+\frac{bc-ad}{c^2+d^2}i$

平方：$(a^2-b^2)+2abi$

最后的拓展：欧拉公式

$e^{i\theta }=\cos \theta +i\sin \theta$

详见 ggb，点击 $n$ 右下角的箭头。（为了不重叠，$e^{i\theta }$ 向左平移 $1$，$\cos \theta +i\sin \theta$ 向右平移 $1$）。

据说当初是欧拉瞪眼法瞪出来的，注意力惊人！

$$e^x=1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+\cdots =\underset{n\to \infty }{\lim }\sum _{i=0}^n\frac{x^i}{i!}$$

$$\sin x=\frac{x}{1!}-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\cdots =\underset{n\to \infty }{\lim }\sum _{i=0}^n(-1{)}^i\times \frac{x^{2i+1}}{(2i+1)!}$$

$$\cos x=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}=\underset{n\to \infty }{\lim }\sum _{i=0}^n(-1{)}^i\times \frac{x^{2i}}{(2i)!}$$

然后就是欧拉的瞪眼：

$$\sin x+\cos x=1-\frac{x}{1!}-\frac{x^2}{2!}+\frac{x^3}{3!}+\frac{x^4}{4!}-\cdots$$

当时复数还没有特别普及，但是欧拉显然知道这一点，所以欧拉：

$$\sin ix+\cos ix=1-\frac{ix}{1!}+\frac{x^2}{2!}-\frac{i{x}^3}{3!}+\frac{x^4}{4!}+\cdots$$

发现出现了复数，继续：

$$i\sin ix+\cos ix=1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+\frac{x^4}{4!}+\cdots =e^x$$

但是在 $\sin$ 和 $\cos$ 的参数里面出现复数不太好，但是可以加到 $e^x$ 中，令 $\theta =ix$：

$$i\sin \theta +\cos \theta =e^{i\theta }$$

证明结束！

return 0;