CF249E Endless Matrix 题解

最新推荐文章于 2024-07-04 16:16:29 发布

larryyu_cs

最新推荐文章于 2024-07-04 16:16:29 发布

阅读量42

点赞数 1

分类专栏： Codeforces 题解文章标签： c++ 算法

本文链接：https://blog.csdn.net/m0_66438282/article/details/133042203

版权

Codeforces 题解专栏收录该内容

10 篇文章 0 订阅

订阅专栏

Description

构造一类矩形：

先构造矩形 $M_1=\begin{bmatrix}1\end{bmatrix}$ 。

对于 $i\geq1$ ， $T_{i+1}$ 从 $T_i$ 构造而来，方法为在最右侧和最下侧插入新的一行一列，自右上到左下 $2 i + 1$ 个数分别填入 $i^2+1,i^2+2\dots(i+1)^2$ 。

比如：

$M_2=\begin{bmatrix}1&2\\4&3\end{bmatrix}$
$M_3=\begin{bmatrix}1&2&5\\4&3&6\\9&8&7\end{bmatrix}$
$M_4=\begin{bmatrix}1&2&5&10\\4&3&6&11\\9&8&7&12\\16&15&14&13\end{bmatrix}$

令左上角坐标为 $(1, 1)$ ，从上至下第 $i$ 行，从左至右第 $j$ 个数的坐标为 $i, j$ 。

共 $T$ 组询问，每次询问 $x_1,y_1,x_2,y_2$ ，求 $\sum_{x_1\le i\le x_2,y_1\le j\le y_2}M_\infty [i][j]$ 。

如果答案在十位数以上，只输出答案的最后十位，前面的数位用 ...代替。

否则输出完整的答案。

前置芝士

两个公式，可以了解一下相关证明：

$1^2+2^2+\dots+n^2=\dfrac{n\times(n+1)\times(2\times n+1)}{6}$

$1+2+\dots+n=\dfrac{(n+1)\times n}{2}$

Solution

对于求一个矩形内所有数值的和，通常运用容斥来转换。

在此题上，设 $S_{x,y}$ 为 $\sum_{1\le i\le x,1\le j\le y}M_\infty [i][j]$ 。

利用容斥： $ans=S_{x_2,y_2}-S_{x_1-1,y_2}-S_{x_2,y_1-1}+S_{x_1-1,y_1-1}$ 。

所以只要会求 $S_{x,y}$ 就好了。

钦定 $y\le x$ 。

对于一个左上角的矩形，其一定包含一个边长为 $y$ 的正方形。

而正方形的和就是 $1+2+\dots+y^2$ ，利用等差数列求和公式得出。

剩下的一部分分类讨论。

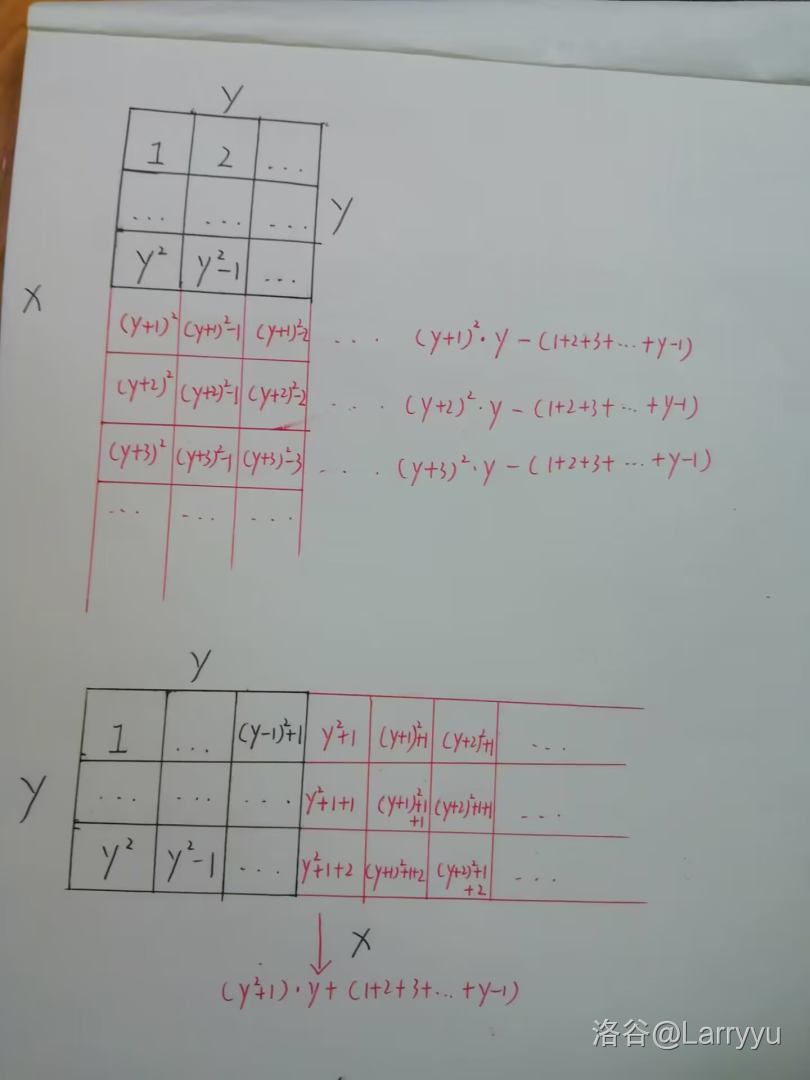
第一种情况，红色部分为 $((y+1)^2+(y+2)^2+\dots+x^2)\times y-(1+2+\dots+y-1)$ 。

第二种情况，红色部分为 $((y^2+(y+1)^2+\dots+(x-1)^2)+(x-y))\times y+(1+2+\dots+y-1)$ 。

很明显，对于 $S_{a,b}$ ，当 $a > b$ 时为第一种情况，当 $a\le b$ 时为第二种情况。

Code

#include<bits/stdc++.h>
using namespace std;
int t;
#define _int __int128  //不能取模，所以开__int128
_int read(){
	_int x=0,f=1;
	char ch=getchar();
	while(ch<'0'&&ch>'9'){
		if(ch=='-') f=-1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9'){
		x=(x<<3)+(x<<1)+ch-'0';
		ch=getchar();
	}
	return x*f;
}
_int calc(_int x){
	if(x==0) return 0;
	return x*(x+1)*(2*x+1)/6;  //平方和公式 
}
_int get(_int x,_int y){
	_int ans=0;
	if(x>y){
		ans+=(y*y+1)*y*y/2;  //正方形 
		_int cnt=calc(x)-calc(y);                
		ans+=cnt*y;
		ans=ans-(x-y)*y*(y-1)/2;
	}else{
		ans+=(x*x+1)*x*x/2;  //正方形 
		_int cnt=calc(y-1)-calc(x-1)+y-x;
		ans+=cnt*x;
		ans=ans+(y-x)*x*(x-1)/2;
	}
	return ans;
}
void print(_int x,int cnt){
	if(cnt==11) return;
	print(x/10,++cnt);
	putchar(x%10+'0');
	
}
void print2(_int x,bool f){
	if(x){
		print2(x/10,0);
		putchar(x%10+'0');
	}else if(f){
		putchar('0');
	}
}
void solve(){
	_int a=read(),b=read(),c=read(),d=read();
	_int ans=((get(c,d)-get(a-1,d))-get(c,b-1))+get(a-1,b-1); //容斥 
	if(ans>=10000000000){
		printf("...");
		print(ans,1);
	}else print2(ans,1);
	printf("\n");
}
int main(){
	t=read();
	while(t--){
		solve();
	}
	return 0;
}