常见电路频域分析

这里有信号吗？

已于 2024-09-19 21:01:35 修改

阅读量592

点赞数 9

文章标签：单片机嵌入式硬件

于 2024-09-19 20:30:56 首次发布

本文链接：https://blog.csdn.net/m0_67648017/article/details/142368653

版权

前言：包括受控源、互感耦合器、桥式电路等，求系统函数，方法有但不限于结点电压法、回路电流法、常规方法等。

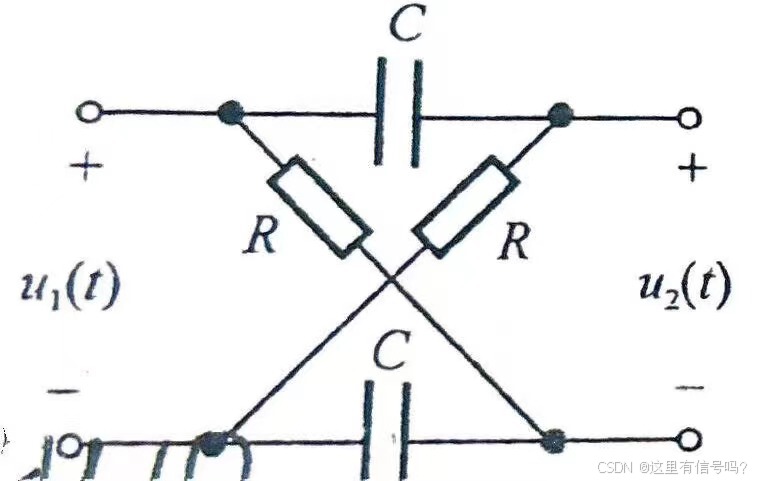
1、桥式电路：

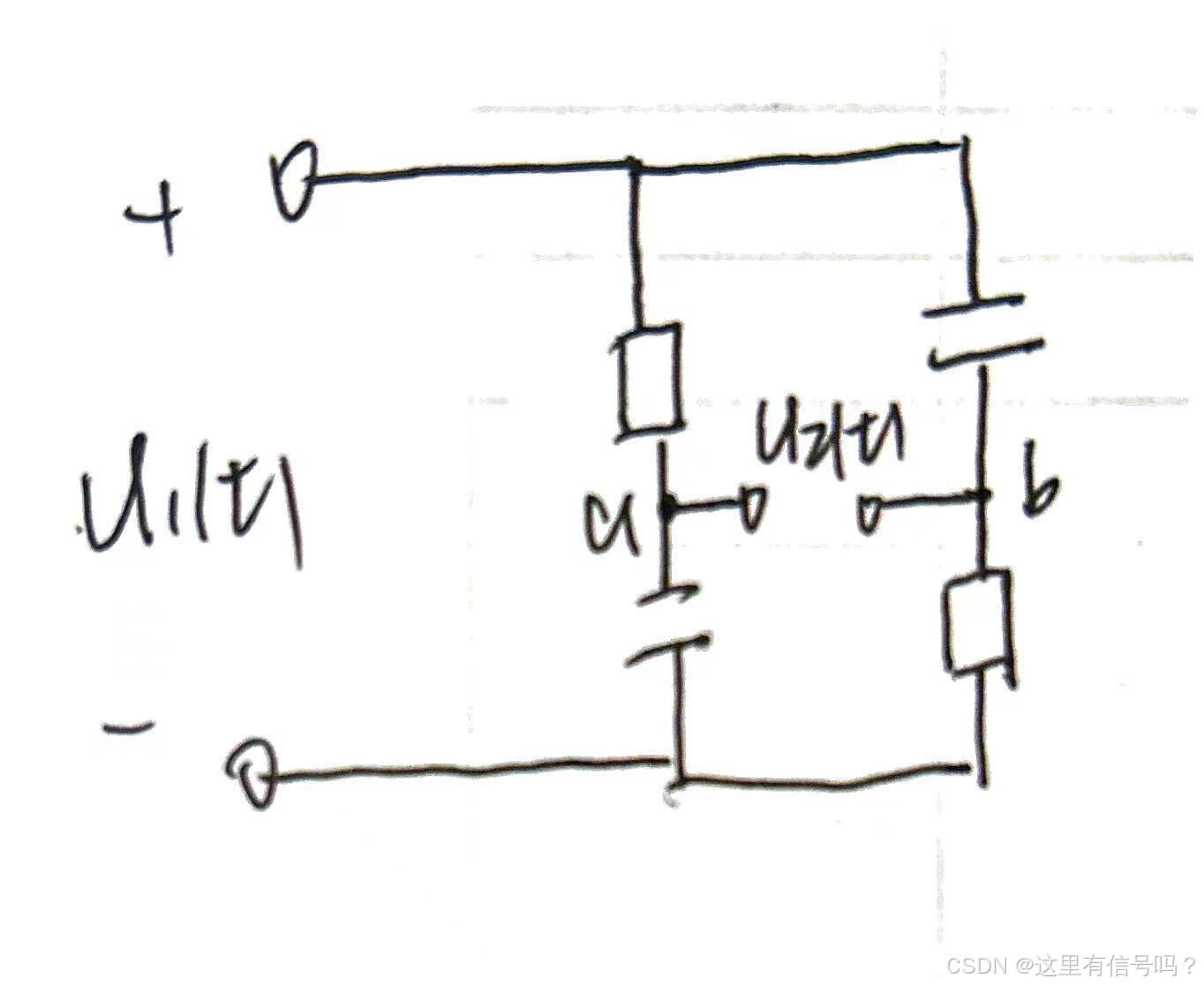
其等效电路为：

思路： $U_2(t)$ 两端电压为 $a,b$ 两点电势差， $a,b$ 两点所在线路并联即电压都为 $U_1(t)$ 。

解： $U_a(s)=\frac{U_1(s)\cdot R}{R+\frac{1}{SC}}$

$U_b(s)=\frac{U_1(s)\cdot \frac{1}{SC}}{R+\frac{1}{SC}}$

$U_2(s)=U_a(s)-U_b(s)=\frac{U_1(s)\cdot (R-\frac{1}{SC})}{R+\frac{1}{SC}}$

即系统函数 $H(s)=\frac{U_2(s)}{U_1(s)}=\frac{s-2}{s+2}$

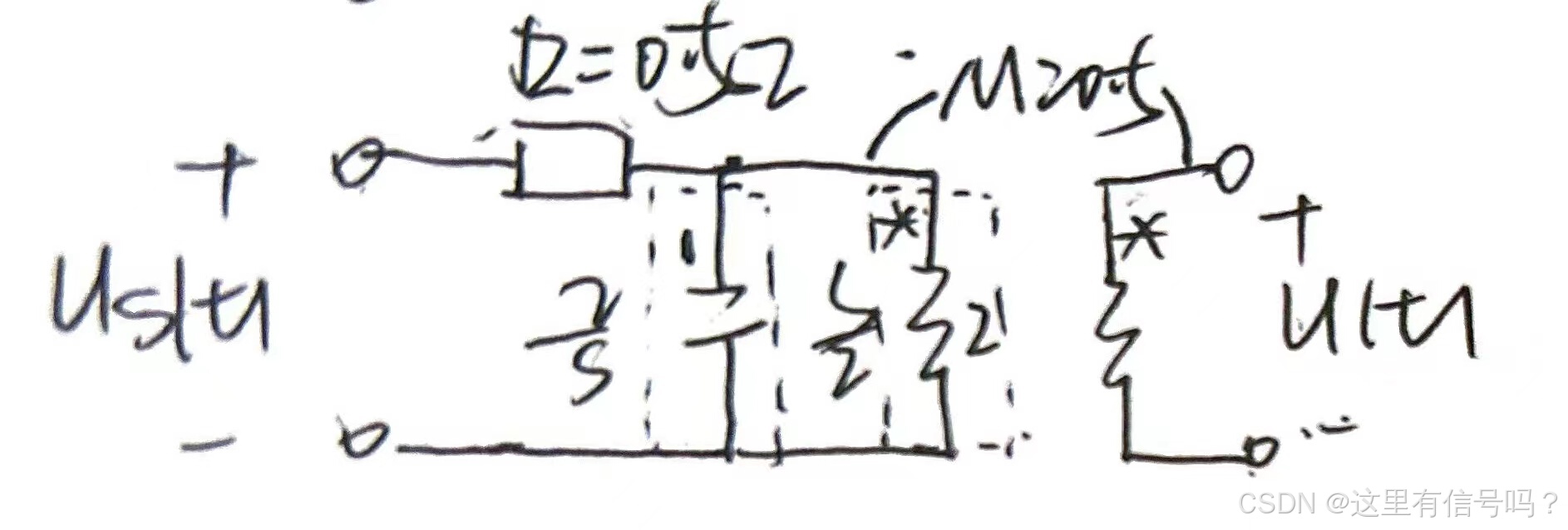
2、互感耦合电路：

思路：需要知道的前提条件 $U(s)=sMI_1$ , $I_1$ 即左边的电感流入电流。首先只考虑左边电路，采用结点电压法（导纳法）列出等式，（ps：不清楚的看我这章节信号与系统——s域之结点电压法_信号与系统求电压-CSDN博客）

解：yw

$(2+\frac{s}{2}+\frac{2}{s})U_1(s)=\frac{U_s(s)}{R}$

$\Rightarrow \frac{(s+2)^2U_1(s)}{2s}=2U_s(s)$

$\Rightarrow U_1(s)=\frac{4sU_s(s)}{(s+2)^2}$

因为 $U(s)=sMI_1$ ，得先求 $I_1$ 而线路1和2并联

所以 $I_1=\frac{U_1(s)}{\frac{s}{2}}=\frac{2U_1(s)}{s}$

$\Rightarrow I_1=\tfrac{8U_s(s)}{(s+2)^2}$

$U(s)=sMI_1$

$\Rightarrow U(s)=\frac{4sU_s(s)}{(s+2)^2}$

而 $H(s)=\frac{U(s)}{U_s(s)}=\frac{4s}{(s+2)^2}$

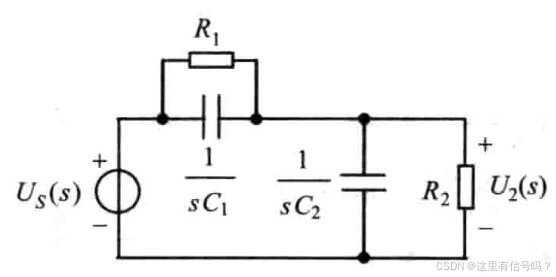
3常规电路：

常规电路图可以采取结点电压法、回路电流法或者微分方程法，以微分方程为例

前提知识：只针对电感有 $U_L(t)=L\frac{di_L(t)}{dt}$ ，而只针对电容有 $i_c(t)=C\frac{du_c(t)}{dt}$

思路：采用电路电流相等，即 $R_1$ 与 $C_1$ 电流和等于 $R_2$ 与 $C_2$ 电流和

解：因为 $R_1$ 与 $C_1$ 并联，所以电压都等于 $U_s(t)-U_2(t)$ ，而 $C_1$ 端电流为 $C_1\frac{d[U_s(t)-U_2(t)]}{dt}$

而 $R_1$ 端电流为 $\frac{U_s(t)-U_2(t)}{R_1}$

$R_2$ 与 $C_2$ 并联，电压都为 $U_2(t)$ ，所以 $R_2$ 端电流为 $\frac{U_2(t)}{R_2}$ ， $C_2$ 端电流为 $C\frac{dU_2(t)}{dt}$

具体过程就不赘述

最后 $H(s)=\frac{6s+1}{12s+3}$