连续模块库

1 微分模块

上图中第一个是连续微分，后面的是离散微分。

连续微分的输入必须是连续信号。

上面的三张图说明了第一点是微分的初始值是从零开始的，第二点是微分的曲线要比原函数的曲线粗糙，所以光滑性比较差的信号比如噪声信号不会采用微分模块。

理想微分模块在物理系统中是不可以实现的，因为实际物理系统具有惯性。，所以MATLAB里的微分模块采用的是下图的形式，c表示惯性常数或者时间常数。

理想微分环节实际上就是一个拉氏算子，在使用时应该尽量和后面的被控信号的传递函数合并

2 状态空间模块

2.1 利用状态空间法求解微分方程

求解微分方程采用高等数学里的解析方法直接求解是方法1，采用拉氏变换求解是方法三

还可以通过下面的信号图利用MATLAB求解，一个技巧是求和输出项应该是最高微分项

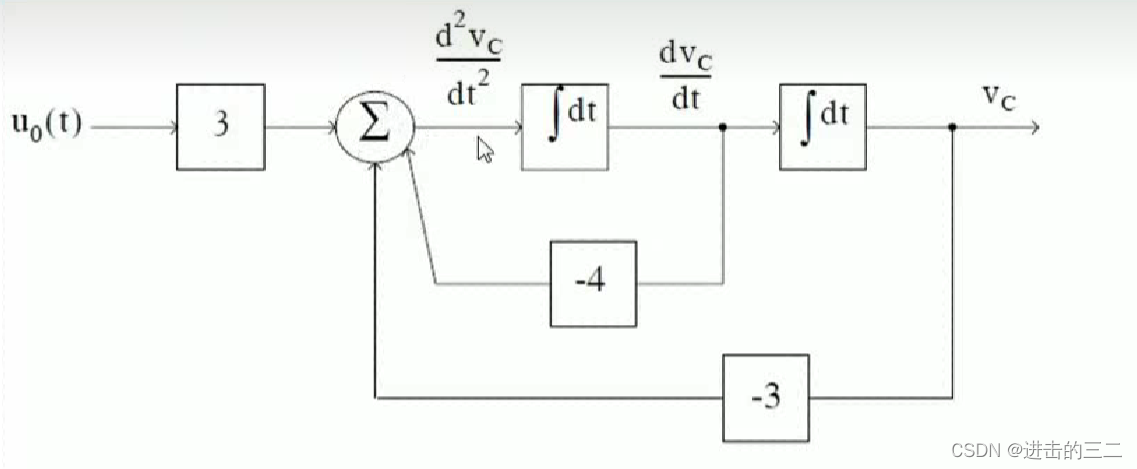
x上面加一点表示对x求导，所以选的矩阵的阶数应该等于求导的最高次数。状态变量x的选取需要凭借经验

下面通过状态空间法利用matlab来求解微分方程

下面的初始条件指的是状态x

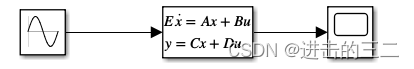
2.2 利用linmod函数提取状态矩阵

对于表示下图左上角的微分方程 ，可以用下图传递函数的形式，传递函数表示一个系统本身的性质，与系统的输入输出没有关系。也可以用下下张图这种框图的形式，用传递函数表示比较好。

通过下面的操作得到了状态矩阵，状态矩阵存储在一个结构体ans里面，之所以要用a=ans.a是为了不改变ans的值。得出的状态矩阵与2.1中的状态矩阵不同，是因为定义的状态变量不在是x1=y

3 传递函数

3.1 tf函数

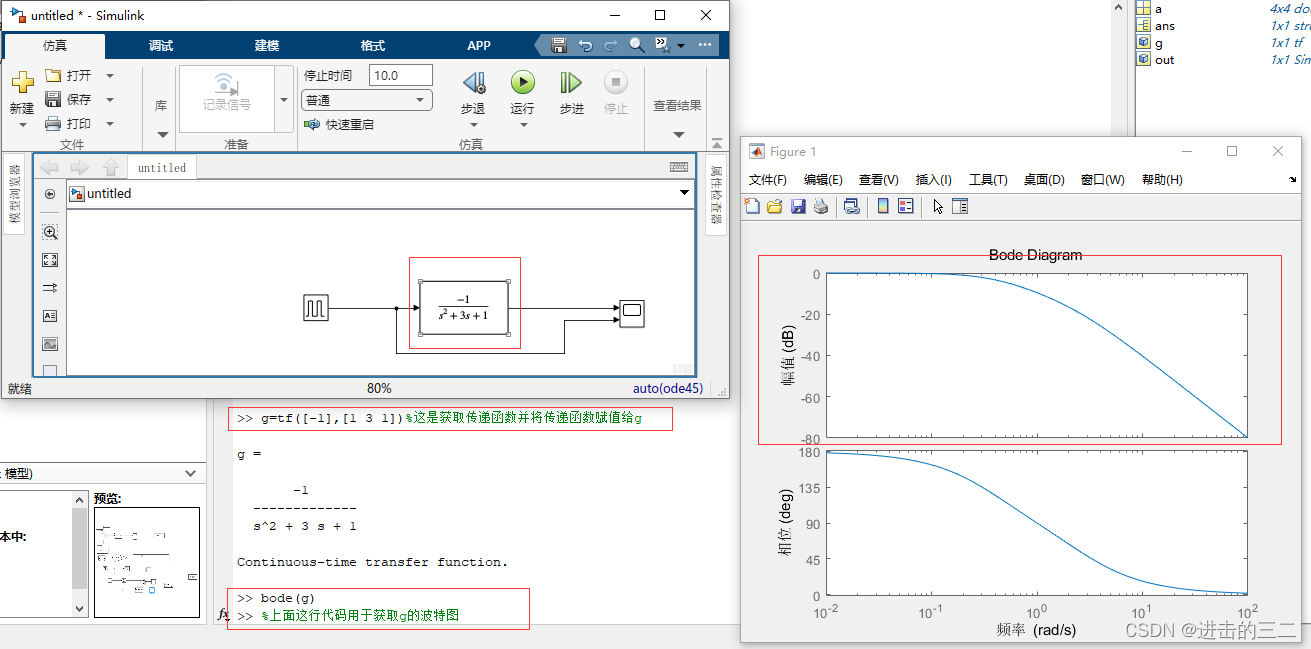
从波特图幅值随频率的变化可以看出，随着频率的升高，赋值降低，所以这是低通滤波器。

如何用系统函数判断高通滤波器
（1）死办法，用傅里叶变换求出H(f)，在画出幅频特性曲线，看高频部分是不是“通”
（2）用拉氏变换求出H(s)，然后记住一句话：分子上有什么就通什么！

举个例子：
H(s)=as/(bs+c)
分子上有“高次”，所以是高通。
这里的“高次”是这个意思：
分母上有s的0次和1次，分子是s的1次，所以是较高的那个，简称“高次”。

H(s)=a/(bs+c)
分子上有“低次”，所以是低通。

H(s)=as^2/ (bs^2+cs+d)+3
分子上有“高次”，所以是高通。

H(s)=a/(bs^2+cs+d)
分子上有“低次”，所以是低通。

H(s)=as/(bs^2+cs+d)
分子上有“中间次”，所以是带通。

3.2 tf、zpk、ss函数的用法

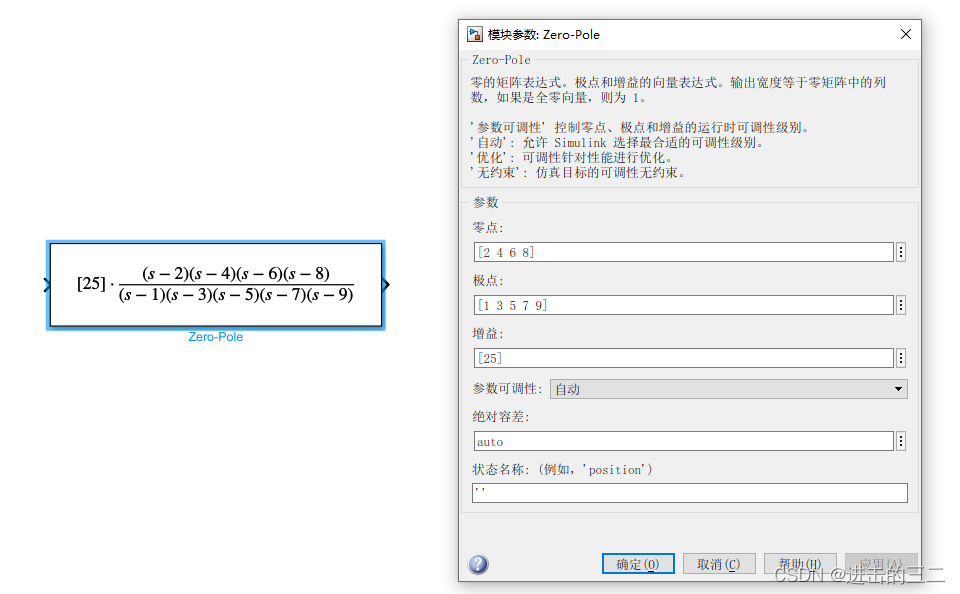
g1=zpk([2 4 6 8],[1 3 5 7 9],25);%zpk创建了零极点形式的传递函数，并将这个函数
% 赋值给g1  zpk的用法是zpk([零点],[极点],增益])
g2=tf(g1);%将零极点形式的传递函数展开
g3=zpk(g2);%将展开的传递函数转换成零极点形式的传函
g4=ss(g1);%将零极点的传递函数转换成状态空间
g5=ss(g2);%将展开的传递函数转换成状态空间
g6=zpk(g4);%将状态空间转换成零极点形式
g7=tf(g5);%将状态空间转换成传递函数形式
g8=ss(g4.A,g4.B,g4.C,g4.D);%这是用四个矩阵来创建状态空间

4 几种延迟模块

我的理解是第一种可以延迟一个固定的时间延时，第二个时间延时可以通过外部给定而第三个时间延时是面向某个问题的原理设置的延时功能，电气用到的应该是前两个吧