量子计算（13）基础知识4：量子测量

最新推荐文章于 2024-07-12 10:47:08 发布

计算机鬼才～

最新推荐文章于 2024-07-12 10:47:08 发布

阅读量2k

点赞数 3

分类专栏：量子计算文章标签：量子计算

本文链接：https://blog.csdn.net/m0_69299019/article/details/130569175

版权

量子计算专栏收录该内容

13 篇文章 60 订阅

订阅专栏

量子测量是量子电路中最后一个元素，在电路中我们经常用到。下面，我将描述量子测量的数学依据以及与量子测量相关的科学定理。

一、量子测量

1、理论知识

测量，好像是一个熟悉又陌生的名词，从小学的时候我们可以用尺子测量长度，到中学时代，学会了物理，开始用各种方法测重力加速度、力或者是其他物理名词。那么，量子态又该如何测量呢？

量子测量由一组测量算子{Mm}描述，这些算子作用在被测量系统的状态空间上。指标m表示在实验中可能出现的测量结果，例如说|0>或者|1>。如果在测量前，量子系统的最新状态是|m>，那么测量结果是m的概率为：

$p(m)=<\psi |M_{m}^{\dagger }M_{m}|\psi >$

并且，测量之后系统的状态为：

$\frac{M_{m}|\psi >}{\sqrt{<\psi |M_{m}^{\dagger }M_{m}|\psi >}}$

测量算子满足完备性方程，即：

$\sum_{m}^{}M_{m}^{\dagger }M_{m}=I$

完备性方程满足了概率和为1的事实，即：

$\sum_{m}^{}<\psi |M_{m}^{\dagger }M_{m}|\psi >=1$

2、计算基下测量单量子比特

在标准基|0>与|1>下测量是较为普遍的，我们以测量单量子比特为例，讲解一下量子测量的计算与结果。这个在单量子比特上的测量有两个结果，由测量算子M0=|0><0|与M1=|1><1|决定。由于M0与M1均为厄尔米特矩阵，即 $M=M^{\dagger }$ ，并且 $M^{2}=M$ ，故满足完备性方程，即：

$I=M_{0}^{\dagger }M_{0}+M_{1}^{\dagger }M_{1}$

假设被测的状态为|q>=a|0>+b|1>，那么测量得到结果0与结果1的概率分别是：

$p(0)=<\psi |M_{0}^{\dagger }M_{0}|\psi >=<\psi| M_{0}|\psi >=|a|^{2}$

$p(1)=<\psi |M_{1}^{\dagger }M_{1}|\psi >=<\psi| M_{1}|\psi >=|b|^{2}$

这两种情况下，测量之后的状态是 $\frac{M_{0}|\psi >}{|a|}=\frac{a\, \, |0>}{|a|}$ 、 $\frac{M_{1}|\psi >}{|b|}=\frac{b\, \, |1>}{|b|}$

例题：已知两个量子态的状态如下：

$|\psi _{1}>=(\frac{3}{5}i,\frac{4}{5})^{T}$ ， $|\psi _{2}>=(\frac{1+i}{\sqrt{3}},\frac{1}{\sqrt{3}})$

求它们分别在基|0>、|1>下的概率。

解析：对于量子态 $|\psi _{1}>$ ， $p(0)=|\frac{3i}{5}|^{2}=\frac{9}{25}$ ， $p(1)=|\frac{4}{5}|^{2}=\frac{16}{25}$ ，对于量子态 $|\psi _{2}>$ ， $p(0)=|\frac{1+i}{\sqrt{3}}|^{2}=\frac{2}{3}$ ， $p(1)=|\frac{1}{\sqrt{3}}|^{2}=\frac{1}{3}$ 。

量子测量最重要的一个定理就是正交可区分，非正交不可区分。

二、两个原理

1、延迟测量原理

原理内容：测量总是可以从量子电路的中间阶段移到电路末端，如果测量结果在电路某个阶段使用，那么经典条件运算可以用量子条件运算来代替。

光看内容不大容易理解，所以小编画了一幅图，希望对大家的理解有帮助！

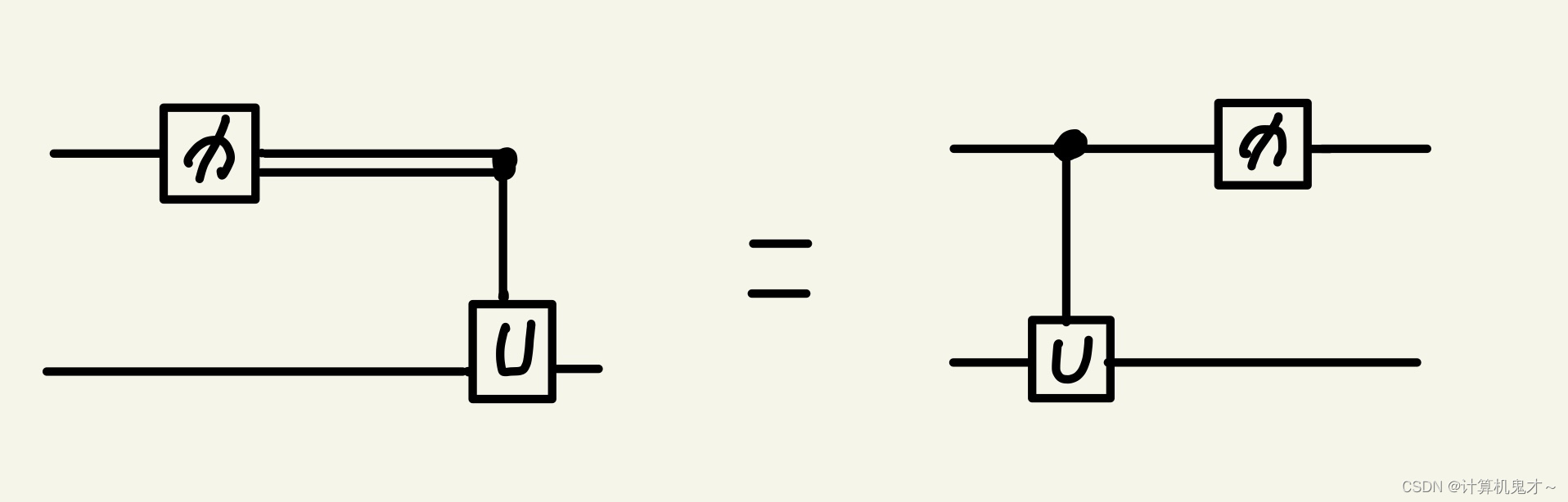
延迟测量的结果是，当被测量的量子比特是一个控制量子比特时，测量与量子门交换。（双线代表这个图中的经典比特）

2、隐含测量原理

原理内容：不失一般性，可以假定在量子电路末端的任何未终止的量子线（未被测量的量子比特）都将被测量。

想象一个只包含两个量子比特的量子电路，电路末端只测量第一个量子比特，此时观测到的测量统计量完全由第一个量子比特的约化密度矩阵决定。然而，如果在第二个量子比特进行了测量，而这种测量能够改变第一个量子比特上的测量统计量，即第一个量子比特的约化密度矩阵不受对第二个量子比特测量的影响。

我们可以证明这一点：设 $\rho$ 是描述两量子比特系统的密度矩阵，假设我们在第二个量子比特的计算基上进行投影测量。设P0=|0><0|，P1=|1><1|分别是第二个量子比特到|0>与|1>的投影。令 $\delta$ 为由不知道测量结果的观察者在测量后赋予系统的密度矩阵，那么，我们可以证明出 $tr(\rho )=tr(\delta )$ ，第一个量子比特的约化密度矩阵不受测量的影响！