【看不懂你来打我]-图论篇11 （tarjan）无向图的桥，无向图的割点，有向图的强连通分量

希望你变强啊

已于 2024-04-26 19:57:03 修改

阅读量1.7k

点赞数 48

分类专栏：图论文章标签：图论算法深度优先数据结构 c++

于 2023-12-02 16:06:51 首次发布

本文链接：https://blog.csdn.net/m0_69478376/article/details/134662860

版权

图论专栏收录该内容

22 篇文章 0 订阅

订阅专栏

讲之前先补充一下必要概念：

预备知识

无向图的【连通分量】：
即极大联通子图，再加入一个节点就不再连通（对于非连通图一定有两个以上的连通分量）

无向图的【(割边或)桥】：
即去掉该边，图就变成了两个连通子图

无向图的【边双连通图】:
无向图中不存在桥，即删除任一条边后仍然连通(每两个点间有至少两条路径，且路径上的边互不重复)

【边双连通分量eDDC】：极大边双连通图

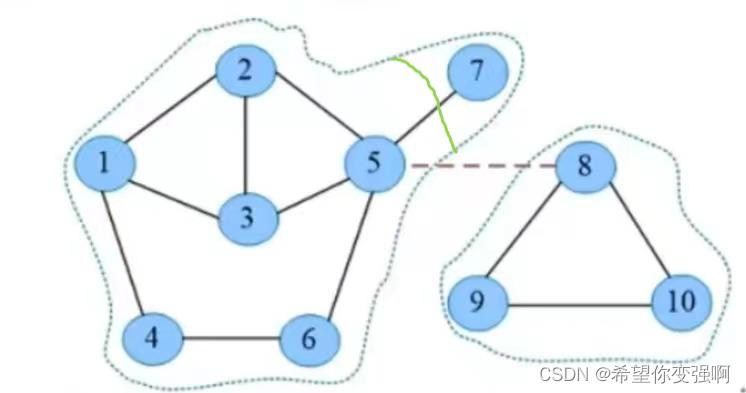
如图：5，7边是桥 5，8边是桥。圈内的就是一个边双联通分量，5和7可不能在一起啊

无向图的【割点】：
将该点和相关联的边去掉，图将变成两个及以上的子图

无向图的【点双连通图】:
无向图中不存在割点，删除任一个点后仍然联通(顶点大于2时，每两个点间有至少两条路径，且路径上的点互不重复)

【点双连通分量vDDC】: 极大点双连通图

如图：5点就是割点。圈内的就是点双联通分量，注意都要包括5点。

注意：有割点不一定有桥，但是有桥一定有割点

请看下图：

虽然5点是割点，但是我们很容易发现5,7是桥 5,8是桥从而画出DAG图

但是有桥不见得可以找到割点。

无向图的【缩点】1：
把每个【eDDC】看成一个点，桥看成连接两个点的无向边，得到一棵树。这种方式称为eDCC缩点

无向图的【缩点】2：
把每个【vDDC】看成一个点，割点看成一个点，每个割点向包含它vDDC连接一条边，得到一棵树。这种方式称为vDCC缩点

我们最常用的是eDDC缩点，因为它的比较简单，也容易实现，所以我会重点讲eDDC缩点

有向图的【强连通分量】：

即极大连通子图（任何两个节点都能相互到达，对比于无向图的极大联通子图）

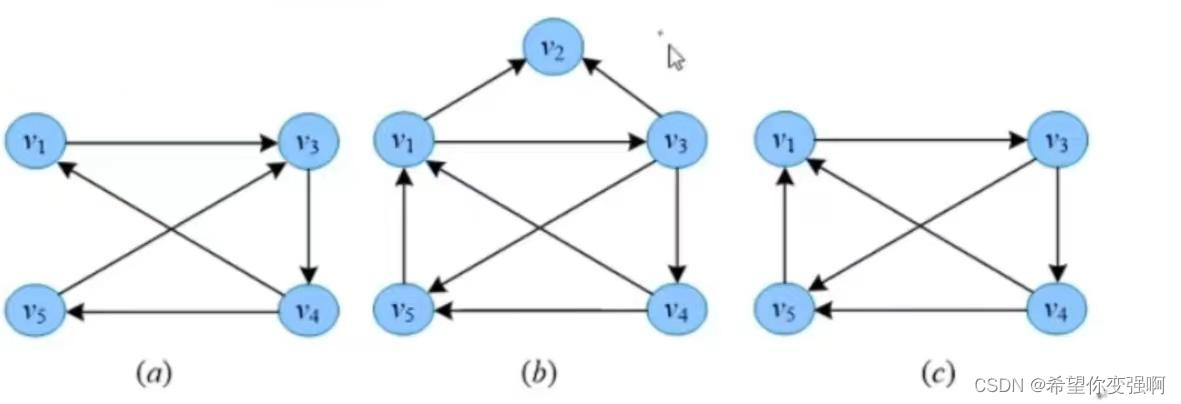
如图：图b中 v1 v3 v4 v5 整体是一个极大连通分量。不能代入v2

模板1：无向图的桥

首先介绍两个树属性：时间戳和回溯点（我更喜欢叫它走回点，听我往下分析）

dfn[u] (时间戳) 表示u节点深度优先遍历最先访问的序号

low[u](走回点)表示u节点或子孙能走回到的最小节点序号

给出结论：

无向边<x,y>是桥，当搜索树上存在x的某个子节点y满足 low[y]>dfn[x]（没有等号）

如何理解呢？

当我们从1点开始dfs的时候，我们走的dfs会把1孩子的节点的dfn和low进行如下标记。

我们不难想到有两种回溯结果，一种是无环回溯，那么这种情况下每个点最终的dfn和low就不会变化（因为孩子的low比自己的low大，所以均不会更新），也就是依然如下图所示。

所以：<1,2><2,3><3,5><5,6><6,4><5,7>都是桥

另一种就是有环回溯，因为4节点再找孩子节点时候发现了1节点，此点来过，就说明既是孩子又是父亲，那么就是遇到了环，此时会更新4节点的low值为1节点的dfn号，然后一直回溯……

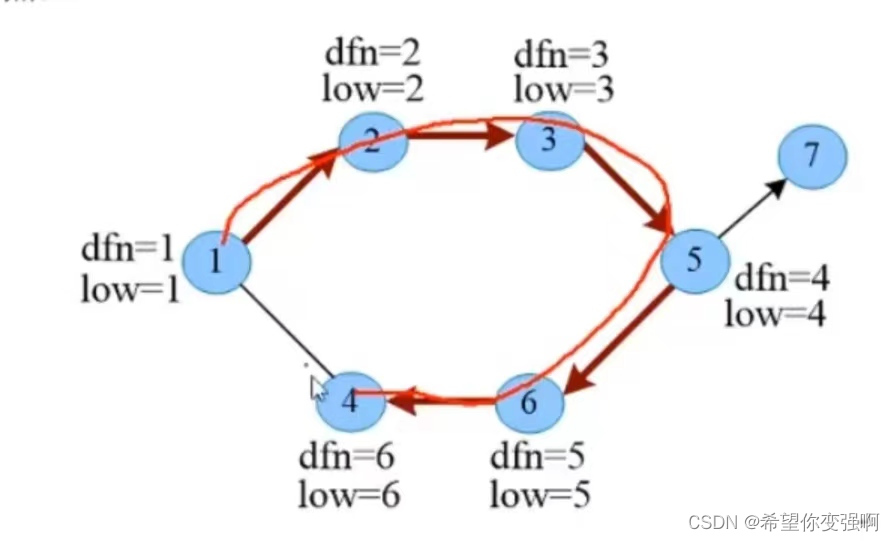
最终结果如下图，整个环上的low号都是1节点的dfn号，而7节点因为遇不到环，所以low不会改变，因此下图就是最终结果。然后我们发现对于5号节点来说，它的孩子的low要比自己的dfn大。

综上所述：就是你不能走父子边回去，也就是怎么来的怎么回去，这样肯定是不行的。我们必须要走非父子边回去的。因为当从非父子边能回去时，也就意味着走到了环，那么此时环点就是能获取的最小dfn号，取值给为low，然后回溯时候父节点获取孩子更小的low即可。

相当于走到环了，那么把这个最小的dfn传遍整个环中，也就是整个连通分量中。从而表示u节点或子孙能走回到的最小节点序号。这样的话同一个连通分量中low值是一样的，是最早走回的点号！（看不懂可以再自己画一下图，就理解了）

对于无向图的桥：孩子的low值比父亲的dfn值大就说明有桥（这个可怜的孩子不能走非父子边回家了，能不可怜吗？？）而且它们的low一定也不相同

void tarjan(int u,int fa){
	dfn[u]=low[u]=++num;//初始化
	for(int i=head[u];i;i=e[i].next){
		int v=e[i].to;
		if(v==fa) continue;//不可以走父子边回去
		if(!dfn[v]){//没访问过就递归访问，访问完要更新low
			tarjan(v,u);
			low[u]=min(low[u],low[v]);//获取孩子最小的low值（low是自己或子孙能走回的最小dfn嘛，不是回溯）
			if(low[v]>dfn[u]){//孩子的low值比父亲的dfn值大说明有桥
				cout<<u<<"- "<<v<<"is bridge "<<'\n';
			}	
		}
		else{//可以从非父子边回去，就要获取dfn值（就是该点能回到的最小dfn，不是回溯）
			low[u]=min(low[u],dfn[v]);
		}
	}
}

这段代码把“回溯大法”体现的很好。可以看到没访问过就递归访问，返回后，也就是等到孩子们的low值都变正确了，我再去更新自己的low。

另外那一句else其实是留给遇环来处理的，父亲节点根本用不上，你只需要在孩子们遇环后把它们自己“照顾好了”之后，借助它们的结果来优化自己就行了。

完整代码

#include <bits/stdc++.h>//无向图的桥
using namespace std;
const int maxn=1000+5;
int n,m;
int head[maxn],cnt;
struct node{int to,next;}e[maxn*2];
int low[maxn],dfn[maxn],num;
//dfn[u](时间戳)表示u节点深度优先遍历访问的序号
//low[u](走回点)表示u节点或子孙能走回到的最小节点序号

void add(int u,int v){ e[++cnt]=(node){v,head[u]};head[u]=cnt;}
void tarjan(int u,int fa){
	dfn[u]=low[u]=++num;//初始化
	for(int i=head[u];i;i=e[i].next){
		int v=e[i].to;
		if(v==fa) continue;//不可以走父子边回去
		if(!dfn[v]){//没访问过就递归访问，访问完要更新low
			tarjan(v,u);
			low[u]=min(low[u],low[v]);//获取孩子最小的low值（low是自己或子孙能走回的最小dfn嘛，不是回溯）
			if(low[v]>dfn[u]){//孩子的low值比父亲的dfn值大说明有桥
				cout<<u<<"- "<<v<<"is bridge "<<'\n';
			}	
		}
		else{//可以从非父子边回去，就要获取dfn值（就是该点能回到的最小dfn，不是回溯）
			low[u]=min(low[u],dfn[v]);
		}
	}
}

void init(){
	memset(head,0,sizeof(head));
	memset(low,0,sizeof(low));
	memset(dfn,0,sizeof(dfn));
	cnt=num=0;
}

int main(){
	while(cin>>n>>m){
		init();
		int u,v;
		while(m--){
			cin>>u>>v;
			add(u,v);
			add(v,u);
		}
		for(int i=1;i<=n;i++){//因为不一定整个图都联通，所以要判断那些点是否走不到
			if(!dfn[i]) tarjan(i,i);//深度优先搜索树的起点就是树根
		}
	}	
}

可以输入数据或自己画图试一下
7 7
1 4
1 2
2 3
3 5
5 7
5 6
6 4
或
7 6
1 2
2 3
3 5
5 7
5 6
6 4

模板2：无向图的割点

x是割点条件：x不是根节点且搜索树上存在x的一个子节点y，满足low[y]>=dfn[x]

【或者】x是根节点且搜索树上存在至少两个子节点满足上述条件 （画图可证明，这里不多说了，而且一般很少用它，主要是上面那个常用，不想看就跳过这个吧）

#include <bits/stdc++.h>//无向图的割点
using namespace std;
const int maxn=1000+5;
int n,m,root;
int head[maxn],cnt;
struct node{int to,next;}e[maxn*2];
int low[maxn],dfn[maxn],num;

void add(int u,int v){ e[++cnt]=(node){v,head[u]};head[u]=cnt;}
void tarjan(int u,int fa){
	dfn[u]=low[u]=++num;//初始化
	int count=0;//记录有几个满足条件的子节点
	for(int i=head[u];i;i=e[i].next){
		int v=e[i].to;
		if(v==fa) continue;//没访问过就递归访问，访问完更新low
		if(!dfn[v]){
			tarjan(v,u);
			low[u]=min(low[u],low[v]);//low是自己或子孙能走回的最小dfn
			if(low[v]>=dfn[u]){
				count++;
				if(u!=root||count>1)cout<<u<<"is gepoint "<<'\n';
			}	
		}
		else{//可以从非父子边回去，就要获取dfn值
			low[u]=min(low[u],dfn[v]);
		}
	}
}

void init(){
	memset(head,0,sizeof(head));
	memset(low,0,sizeof(low));
	memset(dfn,0,sizeof(dfn));
	cnt=num=0;
}

int main(){
	while(cin>>n>>m){
		init();
		int u,v;
		while(m--){
			cin>>u>>v;
			add(u,v);
			add(v,u);
		}
		for(int i=1;i<=n;i++){//因为不一定整个图都联通，所以要判断那些点是否走不到
			if(!dfn[i]) {
				root=i;
				tarjan(i,i);
		}
		}
	}	
}

测试数据（供你参考使用）
7 7
1 4
1 2
2 3
3 5
5 7
5 6
6 4
或
5 3
1 2
2 3
3 5

模板3：有向图的强连通分量

有向图的【强连通分量】：即极大连通子图（任何两个节点都能相互到达）

（说白了就是把整个简单环或复杂环给标记在一起）

这里还是拿来之前的那张图来用啊。这里都看成有向边啊，我就懒得再画了。

当我们从1点开始dfs的时候，我们走的dfs会把1孩子的节点的dfn和low进行如下标记，同时把此点入栈。

我们不难想到有两种回溯结果，一种是无环回溯，那么这种情况下每个点最终的dfn和low就不会变化（因为孩子的low比自己的low大，所以均不会更新），在回溯到每个点的时候，每个点发现自己的low[u]和dfn[u]相等，也就是没有被改变过，就会出栈直到自己也被弹出为止。

所以：1,2,3,4,5,6,7都是强联通分量

回溯到每个点时候，它们发现自己的low被更新了，也就是low不等于dfn，那么就不会出栈，直到回溯到了1的时候，1发现自己的low等于dfn，就会把一直出栈，直到自己也出栈，那么这个时候4,6,5,3,2,1就是一个强联通分量了，7单独是一个强联通分量。

以上内容大多和无向图的桥雷同，为了方便你找重点，我把两者的不同部分用紫色标记出来了。不用谢我。

这里写不着急上代码，我先来个总结：

其实无向图的桥也好，有向图的强联通分量也罢，都是立志于对整个图的点进行划分，我们把有环的点标记在一起，对于无向图，你可以使用边双联通分量中的任何一点的编号去标记（我们更多是祖宗编号），对于有向图也是如此，强联通分量中的每个点都是等价的，使用哪个点的编号都可以（我们一般也是使用祖宗编号）

然后单独给不同标号之间添加入度和出度方便研究整个DAG图，也可以给不同标记之间建立新的对应的指向关系，以此来达到缩点方便图上dp的目的。不过你要考虑到重边的影响，不过大部分是不影响结果的。

核心算法：

前面和无向图基本一样（无非不用跳过走父子边步骤），后面内容就不太一样了。

if(low[u]==dfn[u]){//在回溯之前，在low[u]==dfn[u]时，则从栈中不断弹出节点，直到x出栈停止。弹出的节点就是一个连通分量
		int v;
		do{//输出强连通分量（一定要先执行再判断）
			v=s.top();s.pop();
			cout<<"V: "<<v<<' ';
			ins[v]=0;
		}while(v!=u);//直到和自己不等为止
		cout<<'\n';
	}

判断条件：在low[u]==dfn[u]时，则从栈中不断弹出节点，直到x出栈停止。弹出的节点就是一个连通分量。

#include <bits/stdc++.h>//有向图的强连通分量
using namespace std;
const int maxn=1000+5;
bool ins[maxn];
int n,m;
int head[maxn],cnt;
stack <int> s;
struct node{int to,next;}e[maxn*2];
int low[maxn],dfn[maxn],num;

void add(int u,int v){ e[++cnt]=(node){v,head[u]};head[u]=cnt;}

void tarjan(int u){
	dfn[u]=low[u]=++num;//dfn访问序号，low是能回溯到的最早的dfn
	ins[u]=1;
	s.push(u);//第一次访问节点时候入栈
	for(int i=head[u];i;i=e[i].next){
		int v=e[i].to;
		if(!dfn[v]){//没访问过就递归访问
			tarjan(v);
			low[u]=min(low[u],low[v]);//获取孩子的最小的low值   
		}
		else if(ins[v]){//已经访问过且在栈中获取dfn号
			low[u]=min(low[u],dfn[v]);
		}
	}
	if(low[u]==dfn[u]){//在回溯之前，在low[u]==dfn[u]时，则从栈中不断弹出节点，直到x出栈停止。弹出的节点就是一个连通分量
		int v;
		do{//输出强连通分量（一定要先执行再判断）
			v=s.top();s.pop();
			cout<<"V: "<<v<<' ';
			ins[v]=0;
		}while(v!=u);//直到和自己不等为止
		cout<<'\n';
	}
}

void init(){
	memset(head,0,sizeof(head));
	memset(low,0,sizeof(low));
	memset(ins,0,sizeof(ins));
	memset(dfn,0,sizeof(dfn));
	cnt=num=0;
}

int main(){
	while(cin>>n>>m){
		init();
		int u,v;
		while(m--){
			cin>>u>>v;
			add(u,v);
		}
		for(int i=1;i<=n;i++){//有向图不一定整个图都双向联通，所以要判断那些点是否走不到
			if(!dfn[i]) 	tarjan(i);
		}
	}	
}

参考数据
5 8
1 2
1 3
3 2
3 4
3 5
4 1
4 5
5 1