模糊PID控制：高级一点的PID [基础+代码实例：温控系统]

目录

1. 前言

2. 模糊PID控制的基本原理

2.1 传统PID控制的局限性

2.2 模糊控制的基本思想

2.3 模糊PID控制的结合

3. 模糊PID控制器的实现步骤

3.1 定义模糊变量

3.2 建立模糊规则库

3.3 模糊推理与去模糊化

3.4 更新PID参数

4. Python实现模糊PID控制器

4.1 安装必要的库

4.2 定义模糊变量和隶属函数

4.3 建立模糊规则库

4.4 创建模糊控制系统的模拟器（简单示例:比例项）

4.5 模糊PID控制器的完整代码（还是以温度控制为例）

4.6 运行结果比对 

5. 总结

---

1. 前言

在控制系统中，PID控制是最常用的控制算法之一，但它在面对复杂的非线性系统或参数变化较大的系统时，往往难以达到理想的控制效果。模糊PID控制结合了模糊逻辑和传统PID控制的优点，通过模糊推理调整PID参数，使得控制器能够更好地适应复杂环境。本文将详细介绍模糊PID控制的原理，并通过Python代码实现一个完整的模糊PID控制器，帮助大家理解这一技术的实际应用。

因为基础PID实例也是用的温控系统，所以两者对比更好理解，基础PID温控系统可以参考：

《最最最基础常用的控制：PID【基础＋代码实例：温控系统】》

2. 模糊PID控制的基本原理

2.1 传统PID控制的局限性

传统PID控制器通过比例（P）、积分（I）和微分（D）三个参数来调节控制量，其控制公式为：

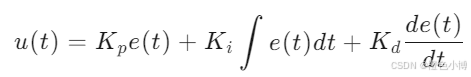
其中，e(t) 是系统的误差信号，Kp​、Ki​ 和 Kd​ 分别是比例、积分和微分系数。然而，PID控制器的性能高度依赖于这三个参数的整定，而在实际应用中，系统参数可能随时间变化，导致PID控制器难以保持良好的控制效果。

2.2 模糊控制的基本思想

模糊控制是一种基于模糊逻辑的控制方法，它通过模糊规则将人类的经验知识转化为控制策略。模糊控制的核心是模糊推理，包括以下几个步骤：

1. 模糊化：将输入的精确值转换为模糊值。

2. 模糊规则库：定义一系列模糊规则，描述输入与输出之间的关系。

3. 模糊推理：根据输入的模糊值和模糊规则进行推理。

4. 去模糊化：将模糊推理的结果转换为精确的输出值。

2.3 模糊PID控制的结合

模糊PID控制通过模糊推理动态调整PID参数（Kp​、Ki​ 和 Kd​），使得控制器能够根据系统的实时状态自动优化参数。具体来说，模糊PID控制器将误差 e(t) 和误差变化率 Δe(t) 作为输入，通过模糊规则调整PID参数，从而实现对复杂系统的有效控制。

3. 模糊PID控制器的实现步骤

3.1 定义模糊变量

模糊变量是模糊控制的基础，通常包括输入变量和输出变量。在模糊PID控制中：

• 输入变量：误差 e(t) 和误差变化率 Δe(t)。

• 输出变量：PID参数的增量 ΔKp​、ΔKi​ 和 ΔKd​。

每个模糊变量需要定义其模糊集合（如“负大”、“负小”、“零”、“正小”、“正大”）以及对应的隶属函数。

3.2 建立模糊规则库

模糊规则库是模糊控制器的核心，它描述了输入与输出之间的关系。例如：

• 如果误差 e(t) 是“正大”且误差变化率 Δe(t) 是“正大”，则 ΔKp​ 是“正大”。

• 如果误差 e(t) 是“零”且误差变化率 Δe(t) 是“零”，则 ΔKp​ 是“零”。

3.3 模糊推理与去模糊化

模糊推理根据输入的模糊值和模糊规则进行推理，得到输出的模糊值。去模糊化则将模糊值转换为精确值，常用的方法包括重心法、最大隶属度法等。

3.4 更新PID参数

根据模糊推理的结果，动态调整PID参数：

4. Python实现模糊PID控制器

4.1 安装必要的库

在实现模糊PID控制器之前，需要安装 skfuzzy 库，这是一个用于模糊逻辑的Python库。

pip install scikit-fuzzy numpy matplotlib

4.2 定义模糊变量和隶属函数

import numpy as np
import skfuzzy as fuzz
from skfuzzy import control as ctrl

# 定义输入变量
e = ctrl.Antecedent(np.arange(-10, 11, 1), 'error')
de = ctrl.Antecedent(np.arange(-10, 11, 1), 'delta_error')

# 定义输出变量
kp = ctrl.Consequent(np.arange(0, 21, 1), 'kp')
ki = ctrl.Consequent(np.arange(0, 21, 1), 'ki')
kd = ctrl.Consequent(np.arange(0, 21, 1), 'kd')

# 定义模糊集合
e.automf(names=['nb', 'ns', 'ze', 'ps', 'pb'])
de.automf(names=['nb', 'ns', 'ze', 'ps', 'pb'])
kp.automf(names=['nb', 'ns', 'ze', 'ps', 'pb'])
ki.automf(names=['nb', 'ns', 'ze', 'ps', 'pb'])
kd.automf(names=['nb', 'ns', 'ze', 'ps', 'pb'])

# 绘制隶属函数
e.view()
de.view()
kp.view()
ki.view()
kd.view()

4.3 建立模糊规则库

# 定义模糊规则
rules = []

# Kp的模糊规则
rules.append(ctrl.Rule(e['nb'] & de['nb'], kp['nb']))
rules.append(ctrl.Rule(e['nb'] & de['ns'], kp['nb']))
rules.append(ctrl.Rule(e['nb'] & de['ze'], kp['ns']))
rules.append(ctrl.Rule(e['nb'] & de['ps'], kp['ze']))
rules.append(ctrl.Rule(e['nb'] & de['pb'], kp['ps']))

rules.append(ctrl.Rule(e['ns'] & de['nb'], kp['nb']))
rules.append(ctrl.Rule(e['ns'] & de['ns'], kp['ns']))
rules.append(ctrl.Rule(e['ns'] & de['ze'], kp['ze']))
rules.append(ctrl.Rule(e['ns'] & de['ps'], kp['ps']))
rules.append(ctrl.Rule(e['ns'] & de['pb'], kp['pb']))

rules.append(ctrl.Rule(e['ze'] & de['nb'], kp['ns']))
rules.append(ctrl.Rule(e['ze'] & de['ns'], kp['ze']))
rules.append(ctrl.Rule(e['ze'] & de['ze'], kp['ze']))
rules.append(ctrl.Rule(e['ze'] & de['ps'], kp['ze']))
rules.append(ctrl.Rule(e['ze'] & de['pb'], kp['ps']))

rules.append(ctrl.Rule(e['ps'] & de['nb'], kp['nb']))
rules.append(ctrl.Rule(e['ps'] & de['ns'], kp['ns']))
rules.append(ctrl.Rule(e['ps'] & de['ze'], kp['ze']))
rules.append(ctrl.Rule(e['ps'] & de['ps'], kp['ps']))
rules.append(ctrl.Rule(e['ps'] & de['pb'], kp['pb']))

rules.append(ctrl.Rule(e['pb'] & de['nb'], kp['nb']))
rules.append(ctrl.Rule(e['pb'] & de['ns'], kp['ns']))
rules.append(ctrl.Rule(e['pb'] & de['ze'], kp['ze']))
rules.append(ctrl.Rule(e['pb'] & de['ps'], kp['ps']))
rules.append(ctrl.Rule(e['pb'] & de['pb'], kp['pb']))

# Ki的模糊规则
rules.append(ctrl.Rule(e['nb'] & de['nb'], ki['nb']))
rules.append(ctrl.Rule(e['nb'] & de['ns'], ki['nb']))
rules.append(ctrl.Rule(e['nb'] & de['ze'], ki['ns']))
rules.append(ctrl.Rule(e['nb'] & de['ps'], ki['ze']))
rules.append(ctrl.Rule(e['nb'] & de['pb'], ki['ps']))

rules.append(ctrl.Rule(e['ns'] & de['nb'], ki['nb']))
rules.append(ctrl.Rule(e['ns'] & de['ns'], ki['ns']))
rules.append(ctrl.Rule(e['ns'] & de['ze'], ki['ze']))
rules.append(ctrl.Rule(e['ns'] & de['ps'], ki['ps']))
rules.append(ctrl.Rule(e['ns'] & de['pb'], ki['pb']))

rules.append(ctrl.Rule(e['ze'] & de['nb'], ki['ns']))
rules.append(ctrl.Rule(e['ze'] & de['ns'], ki['ze']))
rules.append(ctrl.Rule(e['ze'] & de['ze'], ki['ze']))
rules.append(ctrl.Rule(e['ze'] & de['ps'], ki['ze']))
rules.append(ctrl.Rule(e['ze'] & de['pb'], ki['ps']))

rules.append(ctrl.Rule(e['ps'] & de['nb'], ki['nb']))
rules.append(ctrl.Rule(e['ps'] & de['ns'], ki['ns']))
rules.append(ctrl.Rule(e['ps'] & de['ze'], ki['ze']))
rules.append(ctrl.Rule(e['ps'] & de['ps'], ki['ps']))
rules.append(ctrl.Rule(e['ps'] & de['pb'], ki['pb']))

rules.append(ctrl.Rule(e['pb'] & de['nb'], ki['nb']))
rules.append(ctrl.Rule(e['pb'] & de['ns'], ki['ns']))
rules.append(ctrl.Rule(e['pb'] & de['ze'], ki['ze']))
rules.append(ctrl.Rule(e['pb'] & de['ps'], ki['ps']))
rules.append(ctrl.Rule(e['pb'] & de['pb'], ki['pb']))

# Kd的模糊规则
rules.append(ctrl.Rule(e['nb'] & de['nb'], kd['nb']))
rules.append(ctrl.Rule(e['nb'] & de['ns'], kd['nb']))
rules.append(ctrl.Rule(e['nb'] & de['ze'], kd['ns']))
rules.append(ctrl.Rule(e['nb'] & de['ps'], kd['ze']))
rules.append(ctrl.Rule(e['nb'] & de['pb'], kd['ps']))

rules.append(ctrl.Rule(e['ns'] & de['nb'], kd['nb']))
rules.append(ctrl.Rule(e['ns'] & de['ns'], kd['ns']))
rules.append(ctrl.Rule(e['ns'] & de['ze'], kd['ze']))
rules.append(ctrl.Rule(e['ns'] & de['ps'], kd['ps']))
rules.append(ctrl.Rule(e['ns'] & de['pb'], kd['pb']))

rules.append(ctrl.Rule(e['ze'] & de['nb'], kd['ns']))
rules.append(ctrl.Rule(e['ze'] & de['ns'], kd['ze']))
rules.append(ctrl.Rule(e['ze'] & de['ze'], kd['ze']))
rules.append(ctrl.Rule(e['ze'] & de['ps'], kd['ze']))
rules.append(ctrl.Rule(e['ze'] & de['pb'], kd['ps']))

rules.append(ctrl.Rule(e['ps'] & de['nb'], kd['nb']))
rules.append(ctrl.Rule(e['ps'] & de['ns'], kd['ns']))
rules.append(ctrl.Rule(e['ps'] & de['ze'], kd['ze']))
rules.append(ctrl.Rule(e['ps'] & de['ps'], kd['ps']))
rules.append(ctrl.Rule(e['ps'] & de['pb'], kd['pb']))

rules.append(ctrl.Rule(e['pb'] & de['nb'], kd['nb']))
rules.append(ctrl.Rule(e['pb'] & de['ns'], kd['ns']))
rules.append(ctrl.Rule(e['pb'] & de['ze'], kd['ze']))
rules.append(ctrl.Rule(e['pb'] & de['ps'], kd['ps']))
rules.append(ctrl.Rule(e['pb'] & de['pb'], kd['pb']))

4.4 创建模糊控制系统的模拟器（简单示例:比例项）

# 创建模糊控制系统
kp_ctrl = ctrl.ControlSystem(rules)
kp_system = ctrl.ControlSystemSimulation(kp_ctrl)

# 设置输入值
kp_system.input['error'] = 5
kp_system.input['delta_error'] = 3

# 进行模糊推理
kp_system.compute()

# 输出结果
print(f"Kp: {kp_system.output['kp']}")
kp.view(sim=kp_system)

以上就是使用模糊推理的手段的基本示例。

4.5 模糊PID控制器的完整代码（还是以温度控制为例）

import numpy as np
import skfuzzy as fuzz
from skfuzzy import control as ctrl
import matplotlib.pyplot as plt


class FuzzyPIDController:
    def __init__(self, kp_range=(0, 1), ki_range=(0, 0.2), kd_range=(0, 0.1)):
        # 初始化模糊变量
        self.e = ctrl.Antecedent(np.arange(-70, 71, 2), 'error')
        self.de = ctrl.Antecedent(np.arange(-10, 11, 1), 'delta_error')
        self.kp = ctrl.Consequent(np.arange(kp_range[0], kp_range[1] + 1, 0.1), 'kp')
        self.ki = ctrl.Consequent(np.arange(ki_range[0], ki_range[1] + 1, 0.02), 'ki')
        self.kd = ctrl.Consequent(np.arange(kd_range[0], kd_range[1] + 1, 0.01), 'kd')

        # 定义模糊集合
        self.e.automf(names=['nb', 'ns', 'ze', 'ps', 'pb'])
        self.de.automf(names=['nb', 'ns', 'ze', 'ps', 'pb'])
        self.kp.automf(names=['nb', 'ns', 'ze', 'ps', 'pb'])
        self.ki.automf(names=['nb', 'ns', 'ze', 'ps', 'pb'])
        self.kd.automf(names=['nb', 'ns', 'ze', 'ps', 'pb'])

        # 创建模糊规则库
        self.rules = self._create_rules()

        # 创建模糊控制系统
        self.ctrl_system = ctrl.ControlSystem(self.rules)
        self.simulator = ctrl.ControlSystemSimulation(self.ctrl_system)

        # 初始化PID参数
        self.kp_value = 0.5
        self.ki_value = 0.1
        self.kd_value = 0.05
        self.prev_error = 0.0
        self.integral = 0.0

    def _create_rules(self):
        rules = []

        # Kp的模糊规则
        rules.append(ctrl.Rule(self.e['nb'] & self.de['nb'], self.kp['nb']))
        rules.append(ctrl.Rule(self.e['nb'] & self.de['ns'], self.kp['nb']))
        rules.append(ctrl.Rule(self.e['nb'] & self.de['ze'], self.kp['ns']))
        rules.append(ctrl.Rule(self.e['nb'] & self.de['ps'], self.kp['ze']))
        rules.append(ctrl.Rule(self.e['nb'] & self.de['pb'], self.kp['ps']))

        rules.append(ctrl.Rule(self.e['ns'] & self.de['nb'], self.kp['nb']))
        rules.append(ctrl.Rule(self.e['ns'] & self.de['ns'], self.kp['ns']))
        rules.append(ctrl.Rule(self.e['ns'] & self.de['ze'], self.kp['ze']))
        rules.append(ctrl.Rule(self.e['ns'] & self.de['ps'], self.kp['ps']))
        rules.append(ctrl.Rule(self.e['ns'] & self.de['pb'], self.kp['pb']))

        rules.append(ctrl.Rule(self.e['ze'] & self.de['nb'], self.kp['ns']))
        rules.append(ctrl.Rule(self.e['ze'] & self.de['ns'], self.kp['ze']))
        rules.append(ctrl.Rule(self.e['ze'] & self.de['ze'], self.kp['ze']))
        rules.append(ctrl.Rule(self.e['ze'] & self.de['ps'], self.kp['ze']))
        rules.append(ctrl.Rule(self.e['ze'] & self.de['pb'], self.kp['ps']))

        rules.append(ctrl.Rule(self.e['ps'] & self.de['nb'], self.kp['nb']))
        rules.append(ctrl.Rule(self.e['ps'] & self.de['ns'], self.kp['ns']))
        rules.append(ctrl.Rule(self.e['ps'] & self.de['ze'], self.kp['ze']))
        rules.append(ctrl.Rule(self.e['ps'] & self.de['ps'], self.kp['ps']))
        rules.append(ctrl.Rule(self.e['ps'] & self.de['pb'], self.kp['pb']))

        rules.append(ctrl.Rule(self.e['pb'] & self.de['nb'], self.kp['nb']))
        rules.append(ctrl.Rule(self.e['pb'] & self.de['ns'], self.kp['ns']))
        rules.append(ctrl.Rule(self.e['pb'] & self.de['ze'], self.kp['ze']))
        rules.append(ctrl.Rule(self.e['pb'] & self.de['ps'], self.kp['ps']))
        rules.append(ctrl.Rule(self.e['pb'] & self.de['pb'], self.kp['pb']))

        # Ki的模糊规则
        rules.append(ctrl.Rule(self.e['nb'] & self.de['nb'], self.ki['nb']))
        rules.append(ctrl.Rule(self.e['nb'] & self.de['ns'], self.ki['nb']))
        rules.append(ctrl.Rule(self.e['nb'] & self.de['ze'], self.ki['ns']))
        rules.append(ctrl.Rule(self.e['nb'] & self.de['ps'], self.ki['ze']))
        rules.append(ctrl.Rule(self.e['nb'] & self.de['pb'], self.ki['ps']))

        rules.append(ctrl.Rule(self.e['ns'] & self.de['nb'], self.ki['nb']))
        rules.append(ctrl.Rule(self.e['ns'] & self.de['ns'], self.ki['ns']))
        rules.append(ctrl.Rule(self.e['ns'] & self.de['ze'], self.ki['ze']))
        rules.append(ctrl.Rule(self.e['ns'] & self.de['ps'], self.ki['ps']))
        rules.append(ctrl.Rule(self.e['ns'] & self.de['pb'], self.ki['pb']))

        rules.append(ctrl.Rule(self.e['ze'] & self.de['nb'], self.ki['ns']))
        rules.append(ctrl.Rule(self.e['ze'] & self.de['ns'], self.ki['ze']))
        rules.append(ctrl.Rule(self.e['ze'] & self.de['ze'], self.ki['ze']))
        rules.append(ctrl.Rule(self.e['ze'] & self.de['ps'], self.ki['ze']))
        rules.append(ctrl.Rule(self.e['ze'] & self.de['pb'], self.ki['ps']))

        rules.append(ctrl.Rule(self.e['ps'] & self.de['nb'], self.ki['nb']))
        rules.append(ctrl.Rule(self.e['ps'] & self.de['ns'], self.ki['ns']))
        rules.append(ctrl.Rule(self.e['ps'] & self.de['ze'], self.ki['ze']))
        rules.append(ctrl.Rule(self.e['ps'] & self.de['ps'], self.ki['ps']))
        rules.append(ctrl.Rule(self.e['ps'] & self.de['pb'], self.ki['pb']))

        rules.append(ctrl.Rule(self.e['pb'] & self.de['nb'], self.ki['nb']))
        rules.append(ctrl.Rule(self.e['pb'] & self.de['ns'], self.ki['ns']))
        rules.append(ctrl.Rule(self.e['pb'] & self.de['ze'], self.ki['ze']))
        rules.append(ctrl.Rule(self.e['pb'] & self.de['ps'], self.ki['ps']))
        rules.append(ctrl.Rule(self.e['pb'] & self.de['pb'], self.ki['pb']))

        # Kd的模糊规则
        rules.append(ctrl.Rule(self.e['nb'] & self.de['nb'], self.kd['nb']))
        rules.append(ctrl.Rule(self.e['nb'] & self.de['ns'], self.kd['nb']))
        rules.append(ctrl.Rule(self.e['nb'] & self.de['ze'], self.kd['ns']))
        rules.append(ctrl.Rule(self.e['nb'] & self.de['ps'], self.kd['ze']))
        rules.append(ctrl.Rule(self.e['nb'] & self.de['pb'], self.kd['ps']))

        rules.append(ctrl.Rule(self.e['ns'] & self.de['nb'], self.kd['nb']))
        rules.append(ctrl.Rule(self.e['ns'] & self.de['ns'], self.kd['ns']))
        rules.append(ctrl.Rule(self.e['ns'] & self.de['ze'], self.kd['ze']))
        rules.append(ctrl.Rule(self.e['ns'] & self.de['ps'], self.kd['ps']))
        rules.append(ctrl.Rule(self.e['ns'] & self.de['pb'], self.kd['pb']))

        rules.append(ctrl.Rule(self.e['ze'] & self.de['nb'], self.kd['ns']))
        rules.append(ctrl.Rule(self.e['ze'] & self.de['ns'], self.kd['ze']))
        rules.append(ctrl.Rule(self.e['ze'] & self.de['ze'], self.kd['ze']))
        rules.append(ctrl.Rule(self.e['ze'] & self.de['ps'], self.kd['ze']))
        rules.append(ctrl.Rule(self.e['ze'] & self.de['pb'], self.kd['ps']))

        rules.append(ctrl.Rule(self.e['ps'] & self.de['nb'], self.kd['nb']))
        rules.append(ctrl.Rule(self.e['ps'] & self.de['ns'], self.kd['ns']))
        rules.append(ctrl.Rule(self.e['ps'] & self.de['ze'], self.kd['ze']))
        rules.append(ctrl.Rule(self.e['ps'] & self.de['ps'], self.kd['ps']))
        rules.append(ctrl.Rule(self.e['ps'] & self.de['pb'], self.kd['pb']))

        rules.append(ctrl.Rule(self.e['pb'] & self.de['nb'], self.kd['nb']))
        rules.append(ctrl.Rule(self.e['pb'] & self.de['ns'], self.kd['ns']))
        rules.append(ctrl.Rule(self.e['pb'] & self.de['ze'], self.kd['ze']))
        rules.append(ctrl.Rule(self.e['pb'] & self.de['ps'], self.kd['ps']))
        rules.append(ctrl.Rule(self.e['pb'] & self.de['pb'], self.kd['pb']))

        return rules

    def compute(self, error):
        # 计算误差变化率
        delta_error = error - self.prev_error
        self.prev_error = error

        # 设置输入值
        self.simulator.input['error'] = error
        self.simulator.input['delta_error'] = delta_error

        # 进行模糊推理
        self.simulator.compute()

        # 更新PID参数
        self.kp_value = self.simulator.output['kp']
        self.ki_value = self.simulator.output['ki']
        self.kd_value = self.simulator.output['kd']

        # 限制积分项以避免积分饱和
        self.integral += error
        if self.integral > 100:
            self.integral = 100
        elif self.integral < -100:
            self.integral = -100

        # 计算PID控制输出
        self.integral += error
        output = self.kp_value * error + self.ki_value * self.integral + self.kd_value * delta_error
        return output


def temperature_system(current_temp, control, K=0.1, alpha=0.05):
    return current_temp + K * (control - alpha * current_temp)


# 测试模糊PID控制器
if __name__ == "__main__":
    # 创建模糊PID控制器
    controller = FuzzyPIDController()

    # 模拟控制过程
    target_value = 70.0
    current_value = 0.0
    history = []

    for _ in range(200):
        error = target_value - current_value
        control_signal = controller.compute(error)
        current_value=temperature_system(current_value,control_signal)
        history.append(current_value)

    # 绘制控制过程
    plt.plot(history)
    plt.axhline(y=target_value, color='r', linestyle='--')
    plt.xlabel('Time')
    plt.ylabel('Value')
    plt.title('Fuzzy PID Control')
    plt.show()

4.6 运行结果比对 

普通PID控制：

模糊PID控制：

可以看到效果的确好很多！

5. 总结

模糊PID控制结合了模糊逻辑和传统PID控制的优点，能够动态调整PID参数，适应复杂系统的控制需求。通过本文的介绍和Python代码实现，读者可以了解模糊PID控制的基本原理和实现方法。在实际应用中，模糊PID控制可以广泛应用于工业过程控制、机器人控制等领域，为解决复杂控制问题提供了有效的解决方案。

希望本文能够帮助大家更好地理解和应用模糊PID控制技术！如果对模糊控制或PID控制有进一步的问题，欢迎在评论区交流讨论。我是橙色小博，关注我，一起在人工智能领域学习进步！