例一

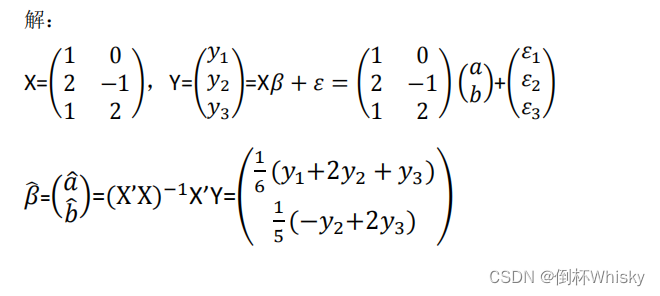
例二
一元线性回归

解:
(1)y=
a
^
\hat{a}
a^+
b
^
\hat{b}
b^x,求线性回归方程即求出
a
^
\hat{a}
a^和
b
^
\hat{b}
b^
而
所以我们首先需要计算
L
x
y
{L_{xy}}
Lxy 和
L
x
x
{L_{xx}}
Lxx:
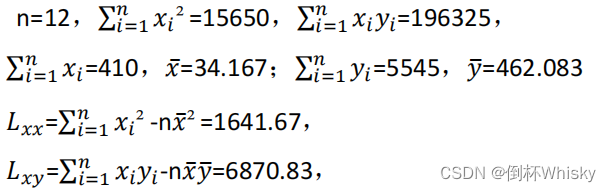
所以 b ^ \hat{b} b^= L x y L x x { {L_{xy}} \over {L_{xx}} } LxxLxy=4.185
a ^ \hat{a} a^= y ˉ \bar{y} yˉ- b ^ x ˉ \hat{b}\bar{x} b^xˉ=319.086
所以回归方程为 y ^ \hat{y} y^=319.086+4.185x
(2)显著性检验需要我们计算出
T
0
{T_0}
T0,所以依次计算出
L
y
y
{L_{yy}}
Lyy、
σ
^
\hat{σ}
σ^,计算得
T
0
{T_0}
T0如下:

而
F
0
{F_0}
F0=
T
0
2
{T_0^2}
T02=14.438>
F
α
{F_α}
Fα(1,n-2)=
F
0.05
{F_{0.05}}
F0.05(1,10)=4.965,因此拒绝
H
0
{H_0}
H0,即:回归效果是显著的。
(3)预测值直接把
x
0
{x_0}
x0=35代入回归方程即可,
y
0
^
\hat{y_0}
y0^=319.086+4.185*35=465.571;
而预测区间需要计算出以下值:
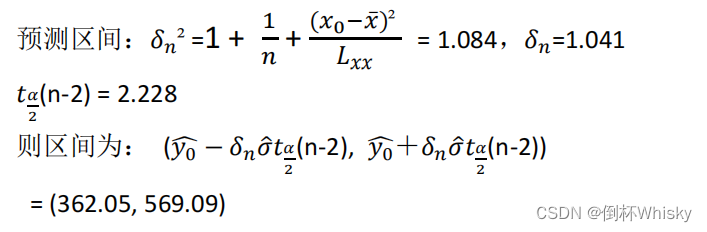
其实难度不大,主要是记住公式就行。
例三
多元线性回归
X= [ 0 0 1 1 1 1 − 1 1 2 0 ] \begin{bmatrix} 0 & 0 \\ 1& 1 \\ 1 &1 \\ -1 &1 \\ 2 & 0 \end{bmatrix} 011−1201110 ,Y= [ 0.01 2.98 3.04 − 1.97 4.96 ] \begin{bmatrix} 0.01 \\ 2.98 \\ 3.04 \\ -1.97 \\ 4.96 \end{bmatrix} 0.012.983.04−1.974.96
设y=
β
1
{β_1}
β1
x
1
{x_1}
x1+
β
2
{β_2}
β2
x
2
{x_2}
x2+ε 求:
(1)试求β;
(2)Y的预测值
Y
^
\hat{Y}
Y^,
ε
^
\hat{ε}
ε^以及残差平方和Q;
(3)决定系数
R
2
{R^2}
R2 和 回归平方和U;
这题可以算是比较典型的一道多元回归了,无论是什么情境下,我们都可以总结出X和Y两个矩阵,题目无非是要我们求β、Q、U和R²,只要记住公式+计算正确一般没什么问题。
解:
求回归方程(Y=Xβ+ε)即 求β和ε,因为X和Y我们可以从题目中总结出来;
首先我们需要求β,记住以下公式:
β = ( X ′ X ) − 1 X ′ Y β={(X'X)^{-1}}X'Y β=(X′X)−1X′Y
X和Y都是已知的,先求X’X,再求其逆矩阵,一般情况下题目给出的都是二阶矩阵,而二阶矩阵的逆矩阵的计算公式为:
A − 1 {A^{-1}} A−1= A ∗ ∣ A ∣ {A^*} \over |A| ∣A∣A∗
即A的伴随矩阵除以A的行列式,而二阶矩阵的伴随矩阵有个口诀是“主交换,副变号”,意思是主对角线的元素对换,副对角线的元素变成其相反数。
所以我们计算得到X’X= [ 7 1 1 3 ] \begin{bmatrix} 7 & 1 \\ 1 & 3 \\ \end{bmatrix} [7113],它的伴随矩阵就是 [ 3 − 1 − 1 7 ] \begin{bmatrix} 3 & -1 \\ -1 & 7 \\ \end{bmatrix} [3−1−17],再除以行列式值为20,所以它的逆矩阵 ( X ′ X ) − 1 {(X'X)^{-1}} (X′X)−1= [ 0.15 − 0.05 − 0.05 0.35 ] \begin{bmatrix} 0.15 & -0.05 \\ -0.05 & 0.35 \\ \end{bmatrix} [0.15−0.05−0.050.35]
接着再依次乘上X’、Y,最终结果为
β = [ 2.484 0.522 ] β=\begin{bmatrix} 2.484 \\ 0.522 \\ \end{bmatrix} β=[2.4840.522]
于是我们就可以把 Y的预测值 计算出来,
Y ^ \hat{Y} Y^=Xβ= [ 0 0 1 1 1 1 − 1 1 2 0 ] \begin{bmatrix} 0 & 0 \\ 1& 1 \\ 1 &1 \\ -1 &1 \\ 2 & 0 \end{bmatrix} 011−1201110 [ 2.484 0.522 ] \begin{bmatrix} 2.484 \\ 0.522 \\ \end{bmatrix} [2.4840.522]= [ 0 3.006 3.006 − 1.962 4.968 ] \begin{bmatrix} 0 \\ 3.006 \\ 3.006\\ -1.962 \\ 4.968 \end{bmatrix} 03.0063.006−1.9624.968
ε ^ \hat{ε} ε^= Y {Y} Y- Y ^ \hat{Y} Y^= [ 0.01 − 0.026 0.034 − 0.008 − 0.008 ] \begin{bmatrix} 0.01\\ -0.026 \\ 0.034\\ -0.008 \\ -0.008 \end{bmatrix} 0.01−0.0260.034−0.008−0.008
残差平方和Q 就是
ε
^
\hat{ε}
ε^中元素的平方和,即:
Q=
ε
^
\hat{ε}
ε^'
ε
^
\hat{ε}
ε^=0.00206
接下来计算 回归平方和U,等于总偏差平方和-残差平方和
通过矩阵Y和Y的均值
Y
ˉ
\bar{Y}
Yˉ我们可以首先把总偏差平方和算出来
TSS=( Y − Y ˉ Y-\bar{Y} Y−Yˉ)'( Y − Y ˉ Y-\bar{Y} Y−Yˉ)
或TSS= Y ′ Y Y'Y Y′Y-n Y 2 ˉ \bar{Y^2} Y2ˉ
用第一个式子算出TSS=30.33252
所以U=TSS-Q=30.33046
决定系数 为
R 2 = U T S S {R^2}={U \over TSS} R2=TSSU
所以 R 2 {R^2} R2=30.33046/30.33252=0.999932

























 8615
8615

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








