说明:本文为本人学习本课程的笔记,课程链接为
【(强推|双字)2022吴恩达机器学习Deeplearning.ai课程】
https://www.bilibili.com/video/BV1Pa411X76sp=8&vd_source=1a7101e2cd4837c57a0824d2cc5a5e56

如需要更深层次地掌握知识,请自行学习视频课程。
第五章 多元线性回归及其梯度下降法(一)
5.1 多维变量
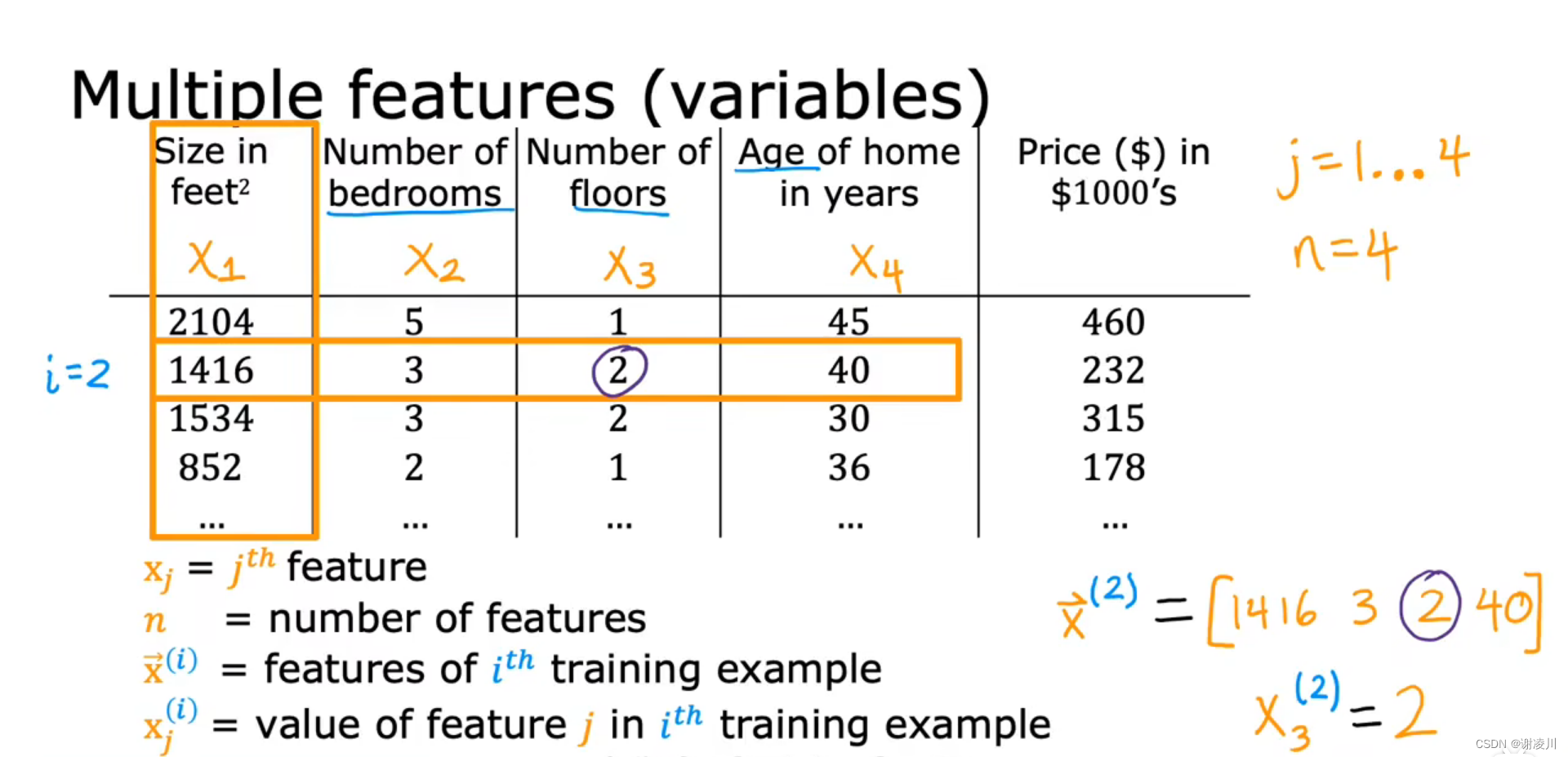
如图,形如
的具有n个维度的变量称为n维向量。
其中 称为向量的第j个特征,n为向量的特征数量,也称为向量的维度。
相对地, 是向量
的第i次迭代 ,
为第i次迭代后向量的第j个特征。
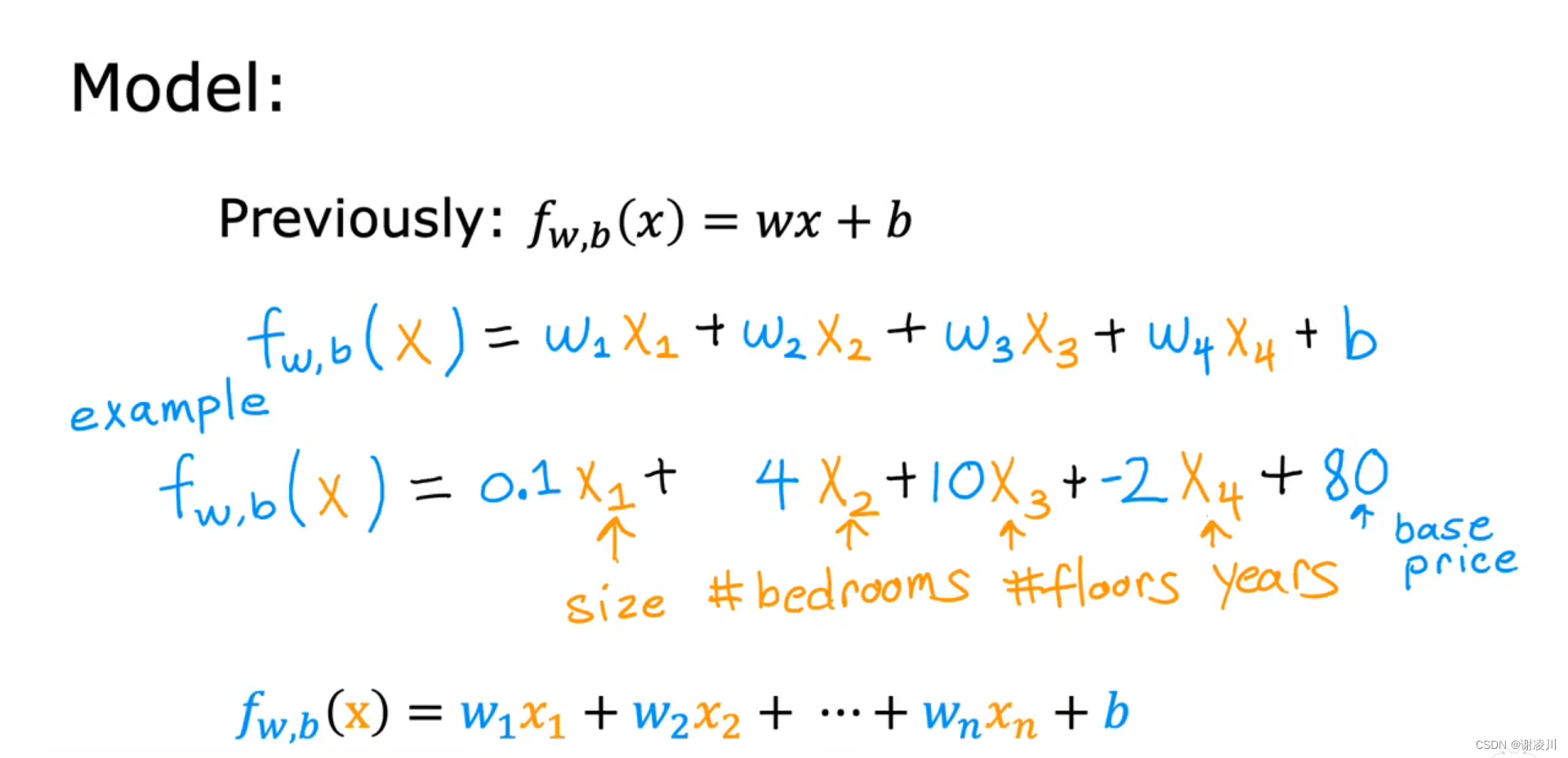
如图, 为一个四元函数,表示了房屋价格受面积、卧室数量、层数、年份四个因素共同作用。其中房屋年份对价格有负面影响,因此
。
当变量数为n时,函数写作
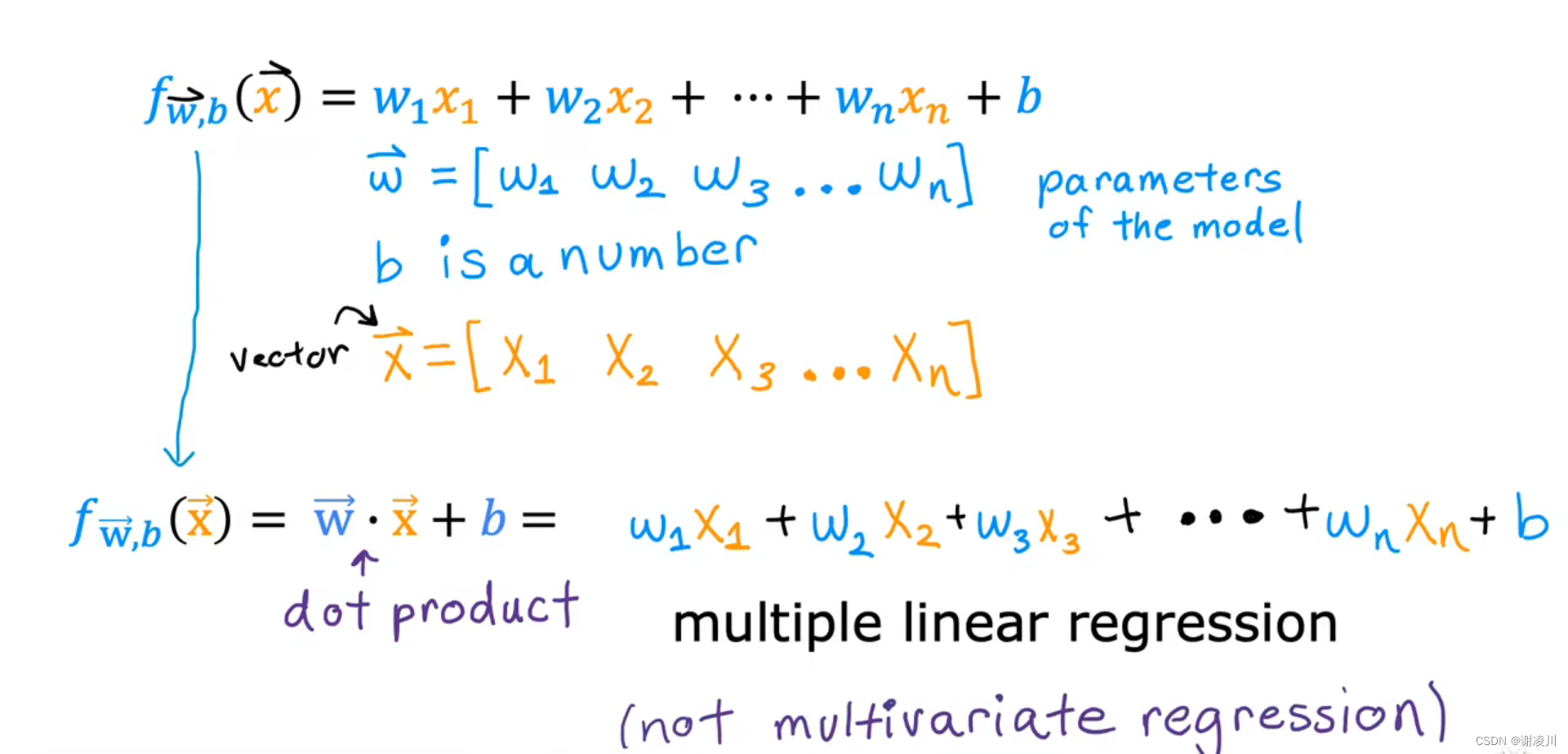
用向量 和
的内积表示函数,有
对这样的函数进行回归计算的过程,称为多元线性回归。
5.2 向量化
在使用numpy库或者各种Tensor张量库进行计算的时候,我们都会感叹这些库计算的速度之快,以至于远远超越自己写的for循环。然后,我们就会逐渐并且越来越多的听说到一个词——vectorization(向量化计算)——其带来了巨大的计算性能。
什么是vectorization?
向量化计算(vectorization),也叫vectorized operation,也叫array programming,说的是一个事情:将多次for循环计算变成一次计算。
————————————————————————————————————————

下面探讨编写函数 f 的计算程序的三种方式
方式1:逐个手动编写
f=w[0]*x[0]+w[1]*x[1]+...+w[n]*x[n]+b方式2:使用for循环
f=0
for j in range(0,n):
f = f + w[j]*x[j]
f = f +b方式3:使用向量
f = np.dot(w,x)+b可以看到,当n较大时,方式1几乎不可行。
而方式2虽然代码相比于方式1更为简洁,但在计算速度上比方式3有较大差距。
在Python的numpy库中使用向量化(Vectorization)计算,速度是非向量化(non-Vectorization)计算(即循环)的700倍(当前开发环境),因为向量化计算使用了python的内建函数,调用了CPU/GPU的SIMD指令集进行计算,大大减少了因为python高级语言执行损耗的时间。
————————————————
版权声明:本文为CSDN博主「PONY LEE」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/weixin_38251332/article/details/120308863
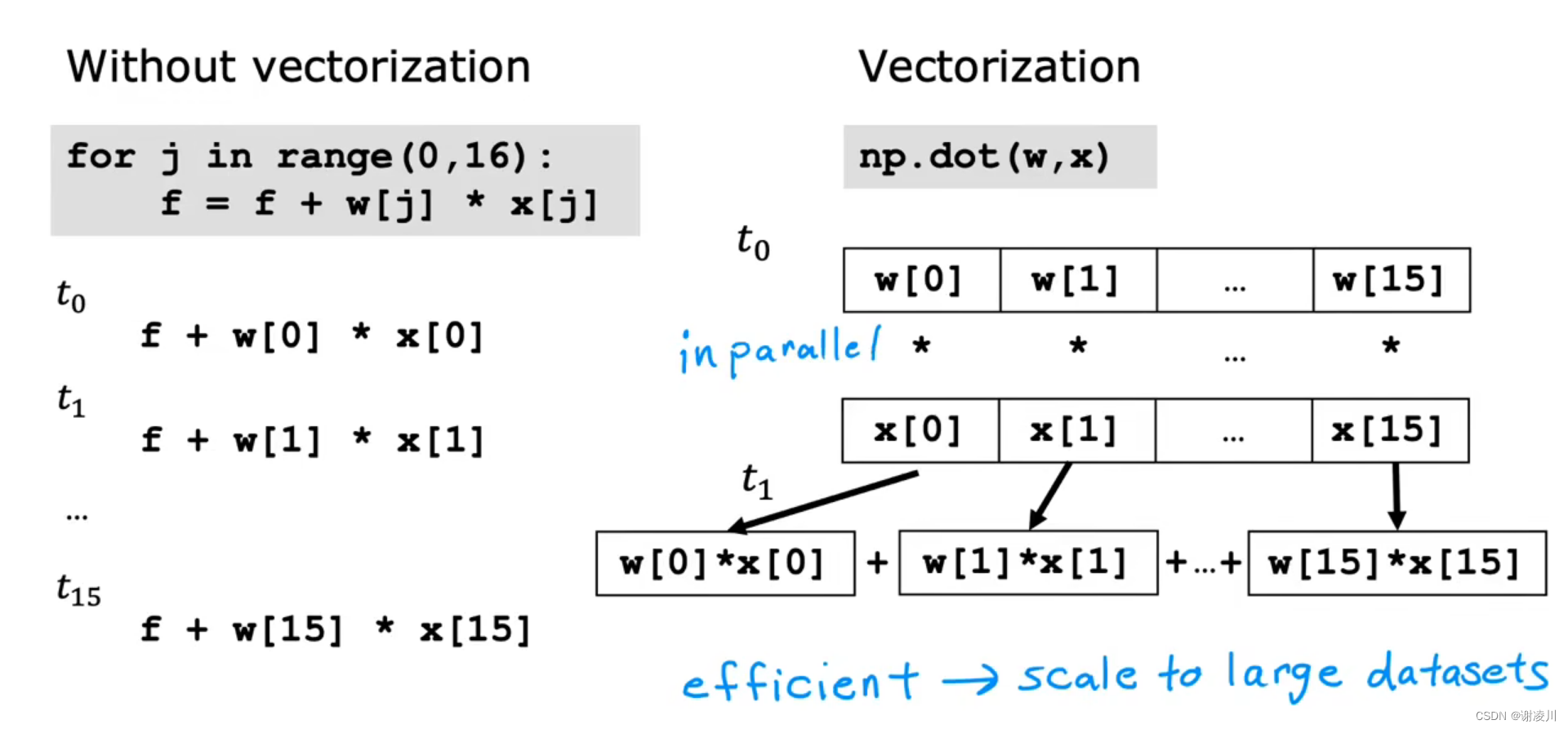

向量化采用了并行的计算方式,能够一次进行向量内积运算,而不需要逐次将参数相乘后相加。
5.3 多元函数的梯度下降法

如图,多元函数的梯度下降以向量和单个参数表示如下。
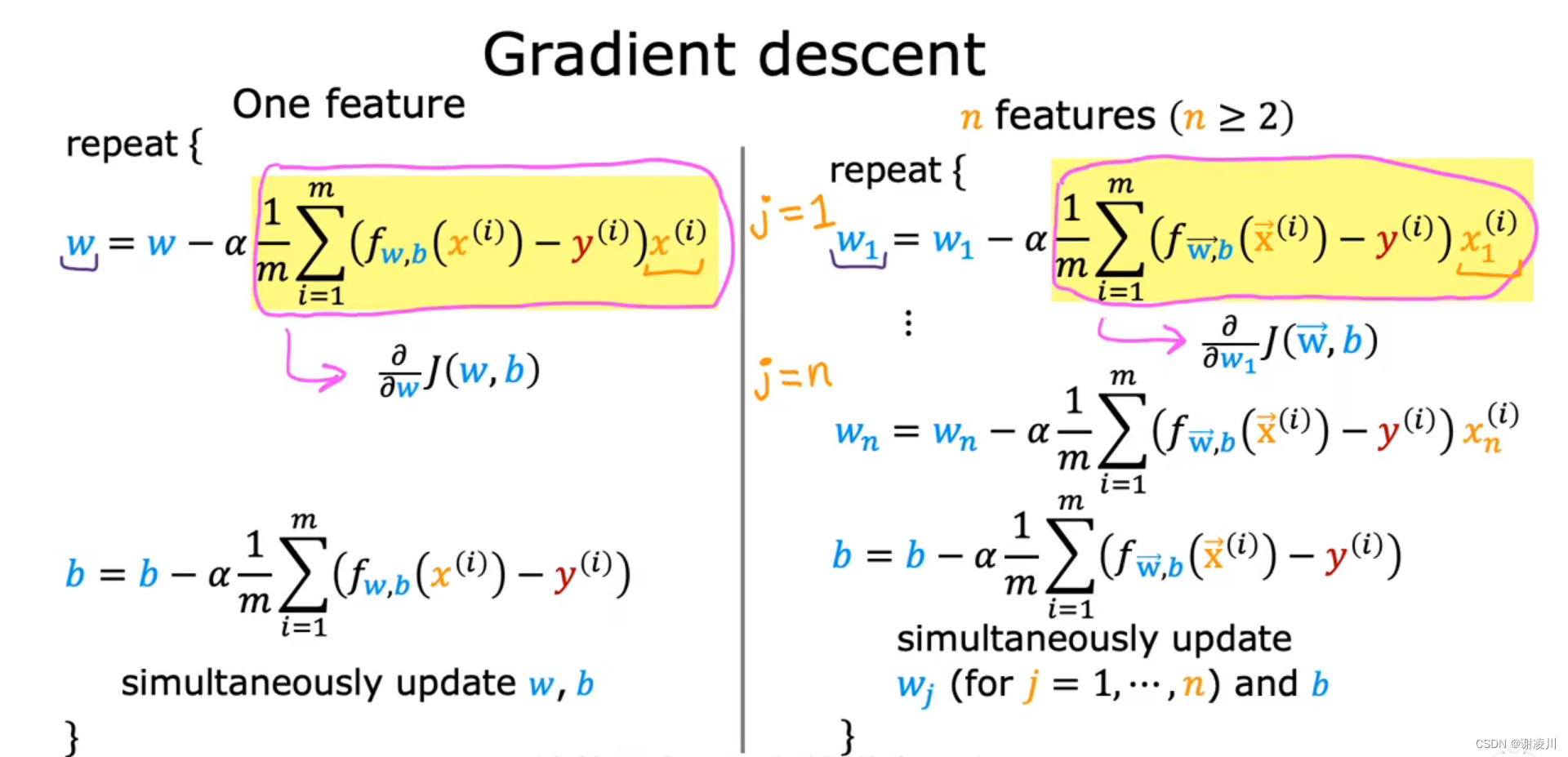
多元线性回归的梯度下降公式如下


除此之外,正规方程是另一种解决线性回归问题的方法,但正规方程法具有一定的局限性。























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








