《昇思25天学习打卡营第12天|量子近似优化算法》

概述

量子近似优化算法（Quantum Approximate Optimization Algorithm，QAOA）是利用量子计算机来近似解决组合优化问题的量子算法，最早由Farhi等人于2014年提出。在本文档里，我们将利用QAOA算法来解决最大割问题（Max-Cut），来熟悉MindSpore Quantum中量子线路的搭建和训练。

环境准备

本文档所需要的额外库：

• networkx

 networkx是创建、操作和研究复杂网络的结构、动态和功能库。可通过如下代码来进行安装。

Max-Cut问题描述

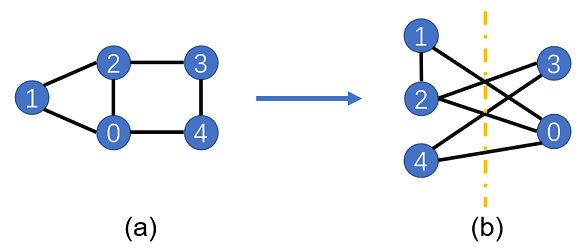
Max-Cut问题是图论中的一个NP-complete问题，它需要将一个图中的顶点分成两部分，并使得两部分被切割的边最多。如下图（a），一个图由五个顶点构成，相互连接的边为(0, 1), (0, 2), (1, 2), (2, 3), (3, 4), (0, 4)。为了使得被切割的边最多，我们尝试通过（b）图的分割，将1、2、4分为一组，0、3分成另一组，因此可得到被切割的边有5条。后面我们将用穷举法验证这个解是否正确。当图中顶点较少时，我们可以在较短时间内通过穷举法找到最大的切割边数，但当图中顶点增多时，我们很难找到有效的经典算法来解决Max-Cut问题，因为这类NP-complete问题很有可能不存在多项式时间算法。但尽管精确解不容易得到，我们却可以想办法在多项式时间内找到问题的一个近似解，这就是近似优化算法。下面，我们介绍怎么将Max-Cut问题转化为一个哈密顿量的基态能量求解问题。

Max-Cut问题量子化

这里我们将图中的每个顶点赋予一个量子比特，当顶点被分到左边时，我们将该顶点上的量子比特设置为|0〉态，同理，右边为|1〉态，当两个顶点被分到不同的集合中时，这两个顶点上的比特将处于不同的量子态。例如对于第0个顶点和第1个顶点，当其连线被切割时，两个顶点上的比特对应的量子态可以表示为|01〉（顶点1：左，顶点0：右）或|10〉（顶点1：右，顶点0：左）；若它们被分到同一边，则对应量子态为|00〉或|11〉。因此我们只要找到一个哈密顿量𝐻𝐻使得：当有连线的两个顶点处于不同量子态时，哈密顿量的期望值为-1，即

〈01|𝐻|01〉=−1,〈10|𝐻|10〉=−1

而当有连线的顶点处于相同量子态时，哈密顿量的期望值为0，即

〈00|𝐻|00〉=0,〈11|𝐻|11〉=0

随后只要使哈密顿量的期望值最小化，就可以找到最大切割边数，以及此时对应的分组情况。之所以将不同量子态时的期望值设为-1，是因为在量子神经网络的训练中，Ansatz中的参数的梯度会一直下降，同时测量值也会一直减少，该训练方法就是以找到最小值为目标，这里我们用它来寻找哈密顿量的基态能量。此时，我们选择哈密顿量𝐻=(𝑍1𝑍0−1)/2，这里𝑍𝑍为泡利𝑍𝑍算符。此时有：

𝑍1𝑍0|00〉=|00〉,𝑍1𝑍0|11〉=|11〉,𝑍1𝑍0|01〉=−|01〉,𝑍1𝑍0|10〉=−|10〉

因此当顶点被分到不同集合时：

〈01||𝐻||01〉=12〈01||𝑍1𝑍0||01〉−12=−1

〈10||𝐻||10〉=12〈10||𝑍1𝑍0||10〉−12=−1

而当顶点被分到同一集合中时，不难验证此时：

〈00||𝐻||00〉=12〈00||𝑍1𝑍0||00〉−12=0

〈11||𝐻||11〉=12〈11||𝑍1𝑍0||11〉−12=0

因此，我们只要对图中的每条边写出上述哈密顿量，然后将所有边求和，即可写出图对应的哈密顿量𝐻𝐻，利用量子计算机求得𝐻𝐻的基态能量与基态，我们就可以得到该图的Max-Cut切割方案与最大切割边数。我们记所有边的集合为𝐶，所有边条数为𝑐，则哈密顿量可写为：

𝐻=∑(𝑖,𝑗)∈𝐶(𝑍𝑖𝑍𝑗−1)/2

导入相关依赖

搭建所需求解的图

通过add_path可在图中添加边。最后画出图的结构。

如上图，我们得到一个由5个节点和6条边构成的图结构。

接下来我们用穷举法来看看所有情况的切割边数。

可以看出，穷举法得到的最大切割边数为5，如果对节点分组的左右进行区分，则一共有4种分组方法可以使切割边数最大，即该问题有4个简并解。

QAOA算法整体流程

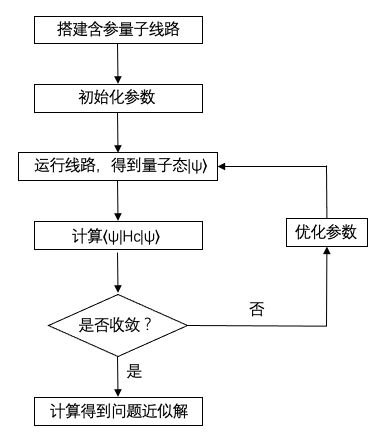
1. 搭建QAOA量子线路，其中ansatz线路包含可以训练的参数
2. 初始化线路中的参数
3. 运行该量子线路，得到量子态|𝜓〉
4. 计算目标哈密顿量𝐻𝐶𝐻𝐶的期望值〈𝜓|𝐻𝐶|𝜓〉
5. 根据第4步的结果，使用Adam优化器优化线路中参数
6. 重复3-5步，直到第4步结果基本不再变化
7. 根据第4步的结果，算出目标问题的近似解

在该流程中，第2-6步都可以由MindSpore和MindSpore Quantum中现成的包和函数来实现，因此我们将重点关注第1步——量子线路的搭建。

搭建QAOA量子线路

先前提到，我们需要将问题对应的哈密顿量

𝐻𝐶=∑(𝑖,𝑗)∈𝐶(𝑍𝑖𝑍𝑗−1)/2

最小化来找到问题的解，也就是说我们要找到该哈密顿量的基态。对此我们可以采用量子绝热演化的方法，使系统先处于某一简单哈密顿量𝐻𝐵的基态上，然后使简单的哈密顿量𝐻𝐵绝热地、缓慢地演化至某一复杂的哈密顿量𝐻𝐶，根据绝热定理，系统将始终保持在哈密顿量的基态上，最终达到复杂哈密顿量𝐻𝐶的基态。

我们将要搭建的量子线路就是采用以上思路，选取初始简单哈密顿量为

𝐻𝐵=∑𝑖−𝑋𝑖

并将量子线路制备到𝐻𝐵𝐻𝐵的基态|𝑠〉=|+〉⊗𝑛，这里通过对所有量子比特作用Hadamard门即可实现。然后连接ansatz含参线路，通过不断地优化其中参数可以使得ansatz线路越来越接近真实绝热演化的效果，最终得到的量子线路可以视为模拟近似了一个真实的绝热演化过程。

ansatz线路

在量子绝热演化中，首先选取初始哈密顿量

并使系统处于𝐻𝐵的基态。然后缓慢地作用如下含时哈密顿量

注意到当𝑡=𝑇𝑡=𝑇时，𝐻(𝑇)=𝐻𝐶。当选取的𝑇𝑇足够大时（满足绝热条件），系统将始终处于𝐻(𝑡)𝐻(𝑡)的瞬时基态上，此时系统的量子态将从初始哈密顿量𝐻𝐵𝐻𝐵的基态|𝜓(0)〉|𝜓(0)〉绝热地演化到目标哈密顿量𝐻𝐶𝐻𝐶的基态|𝜓(𝑇)〉上，即

也就是说，ansatz线路需要模拟的就是这一演化过程。接下来我们将对这个式子进行一些近似和化简，使其变为可以在量子线路中实现的形式。

考虑如下trotter公式

略去𝑂(Δ𝑡2)项，得到

令𝛽𝑙=(1−𝑡𝑙/𝑇)Δ𝑡，𝛾𝑙=𝑡𝑙Δ𝑡/𝑇，并取𝑁𝑁为一个有限大的整数，即得到QAOA的ansatz

因此我们需要搭建的ansatz线路由𝑈𝐶(𝛾)和𝑈𝐵(𝛽)这两个酉变换交替构成，其中𝑈𝐶(𝛾)=𝑒−𝑖𝛾2∑〈𝑖,𝑗〉𝑍𝑖𝑍𝑗可以由 Rzz 门实现，𝑈𝐵(𝛽)=𝑒𝑖𝛽∑𝑖𝑋𝑖则相当于在每个量子比特上作用一个 RX旋转门，𝛾和𝛽是可训练的参数。

搭建𝑈𝐶(𝛾)对应的量子线路：

线路展示：

搭建𝑈𝐵(𝛽)对应的量子线路：

线路展示：

实现了一层酉变换𝑈𝐵(𝛽)𝑈𝐶(𝛾)的ansatz线路如下所示：

为了使得最后优化的结果足够准确，我们需要将量子线路重复多次，因此我们通过如下函数搭建多层的训练网络。

构建图对应的哈密顿量𝐻𝐶=∑(𝑖,𝑗)∈𝐶(𝑍𝑖𝑍𝑗−1)/2（忽略常数项和系数）。

生成完整的量子线路和图所对应的哈密顿量

这里我们选择p = 4，表示选用4层的QAOA量子线路，ansatz是求解该问题的量子线路，init_state_circ是将量子态制备到均匀叠加态（𝐻𝐵𝐻𝐵的基态）上的量子线路。

方法一：利用传统优化算法完成优化搜索

生成梯度算子

首先，我们利用模拟器生成计算QAOA变分量子线路期望值和梯度的运算算子。

grad_ops是一个可以用来计算期望值和期望值关于变分参数的导数的算子，例如我们可以通过如下方式计算线路在参数为 p0 时的期望值和导数。

这里，我们算出来期望值是一个(𝑚=1,𝑛=1)维的数组，其中 𝑚 表示本次运算将多少数据通过编码器编码成了量子态，由于QAOA任务不用编码器，因此𝑚取默认值1，𝑛 表示本次运算计算了多少个哈密顿量期望值（MindQuantum支持多哈密顿量并行处理），此处我们只计算了ham的期望值，所以𝑛=1。同理，对于梯度值来说，它的维度是(𝑚=1,𝑛=1,𝑘=8)，新增的维度𝑘=8表示整个线路中的ansatz变分参数个数。

我们引入scipy中的二阶优化器BFGS来对Max-Cut问题进行优化。

训练过程

BFGS是一个二阶优化器，效果较好。指定jac=True，表示告诉优化器，待优化的函数在返回函数值的同时也会返回梯度值。如设定为False，优化器会利用差分法自行计算近似梯度，这会消耗大量算力。

在最优解时，训练得到的变分参数为：

{'g0': -0.7937405249177704, 'b0': 0.24377670096995407, 'g1': 1.6118673532108145, 'b1': -2.090843525880127, 'g2': -0.2191999657174329, 'b2': -1.9553080941053047, 'g3': 1.2663769840189145, 'b3': 2.7528926560153364}

方法二：利用 MindSpore 机器学习框架完成量子神经网络训练

搭建待训练量子神经网络

由于该问题不需要编码层量子线路，我们这里使用MQAnsatzOnlyLayer作为待训练的量子神经网络，并采用Adam优化器。

训练并展示结果

train step: 0 , cut: [2.9999804]
train step: 10 , cut: [4.188913]
train step: 20 , cut: [4.561035]
train step: 30 , cut: [4.734121]
train step: 40 , cut: [4.8238378]
train step: 50 , cut: [4.8659406]
train step: 60 , cut: [4.8806806]
train step: 70 , cut: [4.9064565]
train step: 80 , cut: [4.9277864]
train step: 90 , cut: [4.938168]
train step: 100 , cut: [4.937685]
train step: 110 , cut: [4.939012]
train step: 120 , cut: [4.9391184]
train step: 130 , cut: [4.939195]
train step: 140 , cut: [4.9392495]
train step: 150 , cut: [4.9392476]
train step: 160 , cut: [4.9392567]
train step: 170 , cut: [4.939256]
train step: 180 , cut: [4.939257]
train step: 190 , cut: [4.939257]
根据上面的训练结果我们发现，该问题哈密顿量的基态能量对应的边切割数趋近于5。

最优参数

前面我们通过训练得到了量子线路中参数的最优值，下面，我们将最优参数提取出来并存储为字典类型，与之前线路中命名的参数一一对应。

{'g0': 0.4488703, 'b0': -1.1391271, 'g1': 0.9061794, 'b1': -0.9447075, 'g2': 1.0675489, 'b2': -0.67761904, 'g3': 1.1678536, 'b3': -0.38241905}

概率图

我们将最优参数代入量子线路，通过对量子线路进行1000次采样，画出最终量子态在计算基矢下的概率分布：

根据概率分布图我们发现，该Max-Cut问题具有四个简并解，每个解对应的概率大概为25%。

• 01001：编号为1、2、4的顶点在左边，编号为0、3的顶点在右边。
• 10110：编号为0、3的顶点在左边，编号为1、2、4的顶点在右边。
• 01011：编号为2、4的顶点在左边，编号为0、1、3的顶点在右边。
• 10100：编号为0、1、3的顶点在左边，编号为2、4的顶点在右边。

可以发现，以上结果与先前通过穷举法得到的结果相符。

总结

这里我们通过量子近似优化算法来解决了Max-Cut问题，并得到了案例中的图对应的最大切割方案。

参考文献

[1] Edward Farhi, Jeffrey Goldstone, and Sam Gutmann. A Quantum Approximate Optimization Algorithm