数据结构Day01

最新推荐文章于 2024-11-16 14:38:00 发布
最新推荐文章于 2024-11-16 14:38:00 发布
阅读量815 收藏 18
点赞数 11
文章标签： 数据结构
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/m0_71729312/article/details/141610164
版权

第1章 顺序表和单链表

1. 基本概念

数据结构是一门研究如何有效组织数据，并提高数据处理效率的学科。通过研究各种数据内
部的逻辑关系，使用某种特定的存储形式，并在此基础上对数据实施各种操作，这些工作被
称为称为广义上的算法。
  • 逻辑结构
    • 指数据之间的内在关系。通常有集合、线性表、树、图等常见的逻辑结构。
    • 逻辑结构是数据之间本身的属性，跟我们怎么处理它们无关。

线性关系：各个元素之间是一种一对一的关系，比如图书馆中的书架的书，除了首尾两本书
之外，其余的任意一本书的编号假设是 N ，都有且仅有一个直接前驱节点 N-1 ，有且仅有一个
直接后继节点 N+1 。这种关系就是典型的线性逻辑。

非线性关系：与上述线性关系的表述不同，如果各个元素之间不是严格一对一的关系，则被
称为非线性关系，比如家族中的各个成员、不同城市间的交通道路等，对于它们中间的某个
元素，都可能有不止一个元素与之关联。这种关系是典型的非线性逻辑。

  • 存储形式
    • 数据的存储方式。比如顺序存储、链式存储等。
    • 不同的存储形式对最终数据的处理效率通常有很大的影响。
    • 逻辑结构与存储形式并无必然联系。

2. 算法分析【了解】

算法分析是指算法在正确的情况下，对其优劣的分析。一个好的算法通常是指：
 
        1. 算法对应的程序所耗时间少
 
        2. 算法对应的程序所耗存储空间少
 
        3. 算法结构性好、易读、易移植和调试

 
数据结构与算法的本质任务，是提高程序的时间空间效率，简单讲就是让程序的执行速度越
快越好，所需内存空间越少越好。虽然在很多情况下，程序的时空特性是相互制约的，就像
鱼和熊掌不可兼得，但我们可以根据程序实际解决问题的侧重点，去平衡时间和空间的对性
能的消耗。

2.1 时间复杂度

一般而言，时间复杂度并不考察一段代码运行所需要的绝对时间，因为不同的计算机的硬件
参数不同，考察绝对时间没有意义。时间复杂度一般指的是代码的语句执行总次数，称为语
句频度。比如： 
void counting(int n)
{
  for (int i = 0; i < n; i++)
  {
    printf("本行语句将会出现n次\n");
    for (int j = 0; j < n; j++)
    {
      printf("本行语句将会出现n*n次\n");
    }
  }
}
在上述代码中，程序执行的语句频度理论是： T(n) = n^2 + n
但一般情况下，我们只关心多项式的最高次幂，于是上述代码的时间复杂度我们表示为：


                                                T(n)=O(n^2)

这意味着，该程序算法所需要的时间，与传进来的参数n的平方成正比。

不同算法的时间复杂度相差很大，如下图所示，随着所处理的问题规模的增大，不同时间复
杂度的程序所需要的时间有天壤之别。

2.2 空间复杂度

空间复杂度的概念更简单一点，就是一段程序运行时所需的内存字节量。
 

2.3 时空复杂度互换

一段程序的性能指标，既要运行快速，又要节省内存，而通常这两者又是相互制约的，很难
兼得。因此在实际解决问题时，会根据需要侧重一方，牺牲另一方。

3. 线性表

3.1 概念

对于一组拥有 n 个数据元素的线性表，其严格数学定义是：其中任何一个数据元素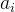a_{i} ，有且仅
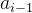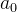有一个直接前驱a_{i-1}，有且仅有一个直接后继a_{i+1}。首元素a_{0}无直接前驱，尾元素a_{n-1}无直接后继。
满足这种数学关系的一组数据，当中的数据是一个挨着一个的，常被称为一对一关系。反之，如果数据之间的关系不是一对一的，就是非线性的。

3.2 举例

生活中的线性表例子非常多，比如一个班级中的以学号编排的学生，一座图书馆中的以序号
编排的图书、一条正常排队等候的队列、一摞从上到下堆叠的餐盘，这些都是线性表。他们
的特点都是：除了首尾两个元素，其余任何一个元素前后都对应相邻的另一个元素。

                            

注意：
 
线性表是一种数据内部的逻辑关系，与存储形式无关
线性表既可以采用连续的顺序存储，也可以采用离散的链式存储

                                

4. 顺序表

4.1 基本概念

  • 顺序表：顺序存储的线性表。
  • 链式表：链式存储的线性表，简称链表。
顺序存储就是将数据存储到一片连续的内存中，在 C 语言环境下，可以是具名的栈数组，或者
是匿名的堆数组。
 
存储方式不仅仅只是提供数据的存储空间，而是必须要能体现数据之间的逻辑关系。当采用
顺序存储的方式来存放数据时，唯一能用来表达数据间本身的逻辑关系的就是存储位置。比
如队列中的两个人，小明和小花，如果小明在逻辑上排在相邻的小花的前面，那么在存储位
置上也必须把小明存放在相邻的小花的前面。

                                        

4.2 基本操作

  • 顺序表设计
    一般而言，为了方便操作顺序表，需要一个专门管理顺序表的 ” 管理结构体 “ ，管理结构体
    中一般会包含：
     
      1. 顺序表总容量
     
      2. 顺序表当前最末元素下标位置
     
      3. 顺序表指针
下面是管理结构体示例代码： 
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
typedef struct
{
  int capacity; // 顺序表容量
  int last;     // 最末元素下标
  int *data;    // 顺序表，以整型数据为例
} sequenceList;
  • 初始化
    所谓初始化就是建立一个不包含任何元素的顺序表，设置好管理结构体中的表的总容量、
    末元素下标，申请好顺序表内存空间等系列准备工作。
下面是初始化顺序表的示例代码： 
sequenceList *init_list(int cap)
{
  sequenceList *list = malloc(sizeof(sequenceList));
  if (list != NULL)
  {
    list->data = malloc(sizeof(int) * cap);
    if (list->data == NULL)
    {
      free(list);
      return NULL;
    }
    list->capacity = cap;
    list->last = -1;
  }
  return list;
}
测试 
int main()
{
  sequenceList *list = init_list(10);

  if (list == NULL)
  {
    perror("初始化顺序表失败!");
    exit(0);
  }
  else
  {
    printf("初始化顺序表成功！\n");
  }
}
  • 增删节点
    在顺序表中增加一个数据，可以有多种方式，比如在原数组的末尾增加，或者在原数组的
    头部增加，或者在数组中间任意一个位置增加。根据实际需要来定。
下面以在顺序表头部增删数据为例，示例代码如下： 
// 判定顺序表是否为空
bool isEmpty(sequenceList *s)
{
  return s->last == -1;
}
// 判定顺序表是否已满
bool isFull(sequenceList *s)
{
  return s->last == s->capacity - 1;
}
// 在顺序表表头插入一个新数据
bool insert(sequenceList *s, int data)
{
  if (isFull(s))
    return false;
  // 将原有数据全部往后挪一位
  for (int i = s->last; i >= 0; i--)
    s->data[i + 1] = s->data[i];
  // 将新数据置入表头
  s->data[0] = data;
  s->last++;
  return true;
}

// 将顺序表表头的数据删除掉
bool removeNode(sequenceList *s)
{
  if (isEmpty(s))
    return false;
  // 将所有数据全部往前挪一位
  for (int i = 0; i < s->last; i++)
    s->data[i] = s->data[i + 1];
  s->last--;
  return true;
}
  • 销毁顺序表

    一个顺序表最后不再需要，应当要释放其所占用的内存空间，这被称为顺序表的销毁。
下面是销毁操作的示例代码： 
void destroy(sequenceList *s)
{
  if (s == NULL)
    return;
  free(s->data);
  free(s);
}

4.3 完整代码

  • seqlist.h 
    #ifndef __SEQLIST_H
#define __SEQLIST_H
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <stdbool.h>
typedef struct
{
  int capacity; // 顺序表容量
  int last;     // 最末元素下标
  int *data;    // 顺序表，以整型数据为例
} sequenceList;
// 初始化顺序表
sequenceList *init_list(int cap);
// 判断顺序表是否写满
bool isFull(sequenceList *list);
// 向顺序表插入数据
bool insert(sequenceList *s, int data);
// 非空校验
bool isEmpty(sequenceList *list);
// 遍历顺序表
void show(sequenceList *list);
// 删除顺序表数据
bool removeNode(sequenceList *list, int data);
// 释放内存
void destroy(sequenceList *s);
#endif
  • seqlist.c 
    #include "seqlist.h"
sequenceList *init_list(int cap)
{
  sequenceList *list = malloc(sizeof(sequenceList));
  if (list != NULL)
  {
    list->data = malloc(sizeof(int) * cap);
    if (list->data == NULL)
    {
      free(list);
      return NULL;
    }
    list->capacity = cap;
    list->last = -1;
  }
  return list;
}
bool isFull(sequenceList *list)
{
  return list->last == list->capacity - 1;
}
// 在顺序表表头插入一个新数据
bool insert(sequenceList *s, int data)
{
  if (isFull(s))
    return false;
  // 将原有数据全部往后挪一位
  for (int i = s->last; i >= 0; i--)
    s->data[i + 1] = s->data[i];
  // 将新数据置入表头
  s->data[0] = data;
  s->last++;
  return true;
}
// 判断是否为空
bool isEmpty(sequenceList *list)
{
  return list->last == -1;
}
// 查看当前顺序表的元素
void show(sequenceList *list)
{
  if (isEmpty(list))
  {
    return;
  }
  for (int i = 0; i <= list->last; i++)
    printf("%d\t", list->data[i]);
  printf("\n");
}
// 将顺序表中指定的某个元素删除掉
bool removeNode(sequenceList *list, int data)
{
  if (isEmpty(list))
    return false;
  // 找到要删除的节点的位置
  int i, pos = -1;
  for (i = 0; i <= list->last; i++)
  {
    if (list->data[i == data])
    {
      pos = i;
      break;
    }
  }
  // 找不到要删除的元素
  if (i > list->last)
  {
    return false;
  }
  // 将所有数据全部往前挪一位
  for (int i = 0; i < list->last; i++)
    list->data[i] = list->data[i + 1];
  list->last--;
  return true;
}
// 释放内存
void destroy(sequenceList *s)
{
  if (s == NULL)
    return;
  free(s->data);
  free(s);
}
int main()
{
  // 创建顺序表
  sequenceList *list = init_list(10);
  if (list == NULL)
  {
    perror("初始化顺序表失败!");
    exit(0);
  }
  else
  {
    printf("初始化顺序表成功！\n");
  }
  // 测试向顺序表插入/删除信息
  int n;
  while (true)
  {
    scanf("%d", &n);
    if (n > 0)
    {
      // 插入
      if (!insert(list, n))
      {
        printf("容量已满，插入失败！\n");
        continue;
      }
    }
    else if (n < 0)
    {
      // 删除
      if (!removeNode(list, -n))
      {
        printf("查无此数，删除失败！\n");
        continue;
      }
    }
    // 遍历
    show(list);
  }
  // 释放
  destroy(list);
}

「课堂练习1」

创建一个顺序表，并从键盘接收数字输入，将输入的正整数按从小到大的顺序插入顺序表，
并在输入负整数的时候将其绝对值数据删除。每次输入后，将顺序表的内容打印到屏幕上。

                                                

解析：
此题考查顺序表的基本思路，先要设计好顺序表的逻辑表达，再通过对顺序表的插入和删除
操作，体会顺序存储中对于插入和删除的不便性。
参考代码 ： 
#include <stdio.h>
#include <stdbool.h>
#include <stdlib.h>
typedef struct
{
  int total_size; // 顺序表总容量
  int last;       // 顺序表最末元素的下标
  int *data;      // 顺序表的存储空间
} sqlist;
// 初始化一个空的顺序表
sqlist *init_list(int total_size)
{
  sqlist *sq = (sqlist *)malloc(sizeof(sqlist));
  if (sq != NULL)
  {
    sq->total_size = total_size;
    sq->last = -1; // 用-1表征当前没有元素
    sq->data = (int *)malloc(sizeof(int) * total_size);
    if (sq->data == NULL)
    {
      free(sq);
    }
  }
  return sq;
}
// 在递增的顺序表中找到x应插入的合适位置
int get_pos(sqlist *sq, int x)
{
  int pos = 0;
  while ((pos <= sq->last) && (sq->data[pos] < x))
    pos++;
  // 当链表为空（即sq->last为-1时），返回0
  return pos;
}
// 判断顺序表是否已满
bool is_full(sqlist *sq)
{
  return sq->last >= sq->total_size - 1;
}
// 将元素x插入顺序表sq中
bool insert(sqlist *sq, int x)
{
  if (is_full(sq))
    return false;
  // 在顺序表中得到即将要插入的元素x的合适的位置
  int pos = get_pos(sq, x);

  // 将顺序表中pos往后的所有元素往后挪一位
  for (int i = sq->last; i >= pos; i--)
    sq->data[i + 1] = sq->data[i];
  sq->data[pos] = x;
  sq->last++;
  return true;
}
// 在顺序表sq中，定位元素x
int locate(sqlist *sq, int x)
{
  int pos;
  for (pos = 0; pos <= sq->last; pos++)
  {
    if (sq->data[pos] == x)
    {
      printf("data[%d]=%d\n", pos, x);
      return pos;
    }
  }
  return -1;
}
// 从顺序表中将元素x剔除
bool delete(sqlist *sq, int x)
{
  int pos;
  pos = locate(sq, x);
  // 元素x不存在
  if (pos == -1)
    return false;
  // 将pos后续的元素全部往前挪一位
  for (; pos <= sq->last; pos++)
    sq->data[pos] = sq->data[pos + 1];
  sq->last--;
  return true;
}
// 展示顺序表元素
void show_data(sqlist *sq)
{
  for (int i = 0; i <= sq->last; i++)
    printf("\tsq->data[%d]=%d\n", i, sq->data[i]);

  printf("=======================\n");
}
int main(int argc, char *argv[])
{
  // 初始化一条空的顺序表
  sqlist *sq = init_list(10);
  // 插入元素
  int num;
  while (1)
  {
    scanf("%d", &num);
    if (num > 0)
    {
      if (insert(sq, num))
        show_data(sq);
      else
        fprintf(stderr, "顺序表已满\n");
    }
    else if (num < 0)
    {
      if (delete (sq, -num))
        show_data(sq);
      else
        fprintf(stderr, "元素不存在\n");
    }
    else
    {
      fprintf(stderr, "BYE\n");
      break;
    }
  }
  return 0;
}

4.4 顺序表优缺点总结

顺序存储中，由于逻辑关系是用物理位置来表达的，因此从上述示例代码可以很清楚看到，
增删数据都非常困难，需要成片地移动数据。顺序表对数据节点的增删操作是很不友好的。
 
总结其特点如下：
 
  • 优点
     
    1. 不需要多余的信息来记录数据间的关系，存储密度高
     
    2. 所有数据顺序存储在一片连续的内存中，支持立即访问任意一个随机数据，比如上述顺序
    表中第i个节点是 s->data[i]
  • 缺点
     
    1. 插入、删除时需要保持数据的物理位置反映其逻辑关系，一般需要成片移动数据
     
    2. 当数据节点数量较多时，需要一整片较大的连续内存空间
     
    3. 当数据节点数量变化剧烈时，内存的释放和分配不灵活

5. 单链表

5.1 基本概念

  • 顺序表：顺序存储的线性表。
  • 链式表：链式存储的线性表，简称链表。
既然顺序存储中的数据因为挤在一起而导致需要成片移动，那很容易想到的解决方案是将数
据离散地存储在不同内存块中，然后在用来指针将它们串起来。这种朴素的思路所形成的链
式线性表，就是所谓的链表。
 
顺序表和链表在内存在的基本样态如下图所示：

                        

5.2 链表的分类

根据链表中各个节点之间使用指针的个数，以及首尾节点是否相连，可以将链表细分为如下
种类：
 
1. 单向链表
 
2. 单向循环链表
 
3. 双向循环链表
 
这些不同链表的操作都是差不多的，只是指针数目的异同。以最简单的单向链表为例，其基
本示意图如下所示：

上图中，所有的节点均保存一个指针，指向其逻辑上相邻的下一个节点（末尾节点指向
空）。另外注意到，整条链表用一个所谓的头指针 head 来指向，由 head 开始可以找到链表
中的任意一个节点。 head 通常被称为 头指针 。
 
链表的基本操作，一般包括：
 
        1. 节点设计
 
        2. 初始化空链表
 
        3. 增删节点
 
        4. 链表遍历
 
        5. 销毁链表
 
下面着重针对这几项常见操作，讲解单向链表的处理。

5.3 单链表节点设计

单向链表的节点非常简单，节点中除了要保存用户数据之外（这里以整型数据为例），只需
要增加一个指向本类节点的指针即可，如下所示： 
typedef int DATA;
typedef struct Node
{
  DATA data;         // 存储数据---数据域
  struct Node *next; // 存储下一个节点的地址---指针域
} NODE;

                                

5.4 单链表初始化

首先，空链表有两种常见的形式。一种是带所谓的头结点的，一种是不带头结点的。所谓的
头结点是不存放有效数据的节点，仅仅用来方便操作，如下：

        ​​​​​​​        ​​​​​​​        

而不带头结点的空链表如下所示：

        ​​​​​​​        ​​​​​​​        

注意：
 
  • 头指针 head 是必须的，是链表的入口
  • 头节点是可选的，为了方便某些操作
由于头结点是不存放有效数据的，因此如果空链表中带有头结点，那么头指针 head 将永远不
变，这会给以后的链表操作带来些许便捷。
 
下面以带头结点的链表为例，展示单向链表的初始化的示例代码： 
/*
@function: int slist_create(NODE** head,DATA data);
@berif: 创建单项链表
@argument: head: 指向头指针变量的地址，用来接收首节点地址
data: 存储在节点中的数据
@return : 成功返回 0
失败返回 -1
*/
int slist_create(NODE **head, DATA data)
{
  NODE *p = (NODE *)malloc(sizeof(NODE));
  if (!p)
  {
    return -1;
  }
  p->data = data;
  p->next = NULL;
  *head = p;
  return 0;
}

5.5 单链表增删节点

相对于顺序表需要整片移动数据，链表增删节点只需要修改几个相关指针的指向，动作非常
快速。
 
与顺序表类似，可以对一条链表中的任意节点进行增删操作，示例代码是： 
/*
@function: int slist_addHead(NODE** head,DATA data);
@berif: 向链表头部插入一个节点数据
@argument: head: 指向头指针变量的地址，用来接收首节点地址
data: 存储在新节点中的数据
@return : 成功返回 0
失败返回 -1
*/
int slist_addHead(NODE **head, DATA data)
{
  NODE *p = (NODE *)malloc(sizeof(NODE));
  if (!p)
  {
    return -1;
  }
  p->data = data;
  p->next = *head;
  *head = p;
  return 0;
}
/*
@function: int slist_addTail(NODE** head,DATA data);
@berif: 向链表尾部插入一个节点数据
@argument: head: 指向头指针变量的地址，用来接收首节点地址
data: 存储在新节点中的数据
@return : 成功返回 0
失败返回 -1
*/
int slist_addTail(NODE **head, DATA data)
{
  NODE *pNew = (NODE *)malloc(sizeof(NODE));
  if (!pNew)
  {
    return -1;
  }
  pNew->data = data;
  pNew->next = NULL;
  NODE *p = *head, *q = NULL;
  if (!p)
  {
    *head = pNew;
    return 0;
  }
  while (p)
  {
    q = p;
    p = p->next;
  }
  q->next = pNew;
  return 0;
}
/*
@function: int slist_insert(NODE** head,DATA pos ,DATA data);
@berif: 向链表节点值为pos的位置插入一个节点数据data
@argument: head: 指向头指针变量的地址
pos: 插入节点位置的节点数据
data: 存储在新节点中的数据
@return : 成功返回 0
失败返回 -1
*/
int slist_insert(NODE **head, DATA pos, DATA data)
{
  NODE *pNew = (NODE *)malloc(sizeof(NODE));
  if (!pNew)
    return -1;
  pNew->data = data;
  pNew->next = NULL;
  NODE *p = *head, *q = NULL;
  if (!p)
  {
    *head = pNew;
    return 0;
  }
  if (memcmp(&(p->data), &pos, sizeof(DATA)) == 0)
  {
    pNew->next = *head;
    *head = pNew;
    return 0;
  }
  while (p)
  {
    if (memcmp(&(p->data), &pos, sizeof(DATA)) == 0)
    {
      pNew->next = p;
      q->next = pNew;
      return 0;
    }
    q = p;
    p = p->next;
  }
  q->next = pNew;
  return 0;
}
/*
@function: int slist_update(const NODE* head,DATA old,DATA newdata);
@berif: 更新链表数据old 为 newdata
@argument: head: 指向头指针变量
old: 待更新的节点数据
newdata: 更新后的节点数据
@return : 成功返回 0
失败返回 -1
*/
int slist_update(const NODE *head, DATA old, DATA newdata)
{
  NODE *p = NULL;
  if (!(p = slist_find(head, old)))
    return -1;
  p->data = newdata;
  return 0;
}
/*
@function: int slist_delete(NODE** head,DATA data);
@berif: 删除链表中节点值为data的节点
@argument: head: 指向头指针变量的地址
data: 删除节点中的数据
@return : 成功返回 0
失败返回 -1
*/
int slist_delete(NODE **head, DATA data)
{
  NODE *p = *head, *q = NULL;
  if (!p)
    return -1;
  if (memcmp(&(p->data), &data, sizeof(DATA)) == 0)
  {
    *head = p->next;
    free(p);
    return 0;
  }
  while (p)
  {
    if (memcmp(&(p->data), &data, sizeof(DATA)) == 0)
    {
      q->next = p->next;
      free(p);
      return 0;
    }
    q = p;
    p = p->next;
  }
  return -1;
}
注意:
 
删除链表的节点并不意味着释放其内存，而是将其剔除出链表

5.6 单链表的遍历

遍历的意思就是逐个访问每一个节点，对于线性表而言，由于路径唯一的选择就是从头走到
尾。因此相当而言比较简单。
 
下面是单向链表的遍历示例代码，假设遍历每个节点并将其整数数据输出： 
/*
@function: NODE* slist_find(const NODE* head,DATA data);
@berif: 查找链表数据data
@argument: head: 指向头指针变量
data: 待查找的数据
@return : 成功返回节点的地址
失败返回NULL
*/
NODE *slist_find(const NODE *head, DATA data)
{
  const NODE *p = head;
  while (p)
  {
    if (memcmp(&(p->data), &data, sizeof(DATA)) == 0)
    {
      return (NODE *)p;
    }
    p = p->next;
  }
  return NULL;
}
/*
@function: void slist_showAll(const NODE* head);
@berif: 遍历链表数据
@argument: head: 指向头指针变量
@return : 无
*/
void slist_showAll(const NODE *head)
{
  const NODE *p = head;
  while (p)
  {
    printf("%d ", p->data);
    p = p->next;
  }
  printf("\n");
}

5.7 单链表的销毁

由于链表中的各个节点被离散地分布在各个随机的内存空间，因此销毁链表必须遍历每一个
节点，释放每一个节点。
注意：
 
销毁链表时，遍历节点要注意不能弄丢相邻节点的指针

示例代码如下： 
/*
@function: void slist_destroy(NODE** head);
@berif: 回收链表
@argument: head: 指向头指针变量的地址
@return : 无
*/
void slist_destroy(NODE **head)
{
  NODE *p = *head, *q = NULL;
  while (p)
  {
    q = p;
    p = p->next;
    free(q);
  }
  *head = NULL;
}
注意：我们可以使用 valgrind 进行内存检测，举例： 
valgrind ./..

5.8 完整代码

  • singleList.h 
    #ifndef __SINGLELIST_H
#define __SINGLELIST_H
// 头文件
#include <stdlib.h>
#include <stdio.h>
#include <string.h>
typedef int DATA;
typedef struct node
{
  DATA data;
  struct node *next;
} NODE;
// 链表创建
int slist_create(NODE **, DATA);
// 链表数据添加-头插法
int slist_addHead(NODE **head, DATA data);
// 链表数据添加-尾插法
int slist_addTail(NODE **head, DATA data);
// 链表数据添加-中间插法
int slist_insert(NODE **head, DATA pos, DATA data);
// 链表数据查询
NODE *slist_find(const NODE *head, DATA data);
// 链表数据更新
int slist_update(const NODE *head, DATA old, DATA newdata);
// 链表数据遍历
void slist_showAll(const NODE *head);
// 链表数据删除
int slist_delete(NODE **head, DATA data);
// 链表回收
void slist_destroy(NODE **head);

#endif
  • singleList.c 
    #include "singleList.h"
/*
@function: int slist_create(NODE** head,DATA data);
@berif: 创建单项链表
@argument: head: 指向头指针变量的地址，用来接收首节点地址
data: 存储在节点中的数据
@return : 成功返回 0
失败返回 -1
*/
int slist_create(NODE **head, DATA data)
{
  NODE *p = (NODE *)malloc(sizeof(NODE));
  if (!p)
  {
    return -1;
  }
  p->data = data;
  p->next = NULL;
  *head = p;
  return 0;
}
/*
@function: int slist_addHead(NODE** head,DATA data);
@berif: 向链表头部插入一个节点数据
@argument: head: 指向头指针变量的地址，用来接收首节点地址
data: 存储在新节点中的数据
@return : 成功返回 0
失败返回 -1
*/
int slist_addHead(NODE **head, DATA data)
{
  NODE *p = (NODE *)malloc(sizeof(NODE));
  if (!p)
  {
    return -1;
  }
  p->data = data;
  p->next = *head;
  *head = p;
  return 0;
}
/*
@function: int slist_addTail(NODE** head,DATA data);
@berif: 向链表尾部插入一个节点数据
@argument: head: 指向头指针变量的地址，用来接收首节点地址
data: 存储在新节点中的数据
@return : 成功返回 0
失败返回 -1
*/
int slist_addTail(NODE **head, DATA data)
{
  NODE *pNew = (NODE *)malloc(sizeof(NODE));
  if (!pNew)
  {
    return -1;
  }
  pNew->data = data;
  pNew->next = NULL;
  NODE *p = *head, *q = NULL;
  if (!p)
  {
    *head = pNew;
    return 0;
  }
  while (p)
  {
    q = p;
    p = p->next;
  }
  q->next = pNew;
  return 0;
}
/*
@function: int slist_insert(NODE** head,DATA pos ,DATA data);
@berif: 向链表节点值为pos的位置插入一个节点数据data
@argument: head: 指向头指针变量的地址
pos: 插入节点位置的节点数据
data: 存储在新节点中的数据
@return : 成功返回 0
失败返回 -1
*/

int slist_insert(NODE **head, DATA pos, DATA data)
{
  NODE *pNew = (NODE *)malloc(sizeof(NODE));
  if (!pNew)
    return -1;
  pNew->data = data;
  pNew->next = NULL;
  NODE *p = *head, *q = NULL;
  if (!p)
  {
    *head = pNew;
    return 0;
  }
  if (memcmp(&(p->data), &pos, sizeof(DATA)) == 0)
  {
    pNew->next = *head;
    *head = pNew;
    return 0;
  }
  while (p)
  {
    if (memcmp(&(p->data), &pos, sizeof(DATA)) == 0)
    {
      pNew->next = p;
      q->next = pNew;
      return 0;
    }
    q = p;
    p = p->next;
  }
  q->next = pNew;
  return 0;
}
/*
@function: NODE* slist_find(const NODE* head,DATA data);
@berif: 查找链表数据data
@argument: head: 指向头指针变量
data: 待查找的数据
@return : 成功返回节点的地址
失败返回NULL
*/
NODE *slist_find(const NODE *head, DATA data)
{
  const NODE *p = head;
  while (p)
  {
    if (memcmp(&(p->data), &data, sizeof(DATA)) == 0)
    {
      return (NODE *)p;
    }
    p = p->next;
  }
  return NULL;
}
/*
@function: int slist_update(const NODE* head,DATA old,DATA newdata);
@berif: 更新链表数据old 为 newdata
@argument: head: 指向头指针变量
old: 待更新的节点数据
newdata: 更新后的节点数据
@return : 成功返回 0
失败返回 -1
*/
int slist_update(const NODE *head, DATA old, DATA newdata)
{
  NODE *p = NULL;
  if (!(p = slist_find(head, old)))
    return -1;
  p->data = newdata;
  return 0;
}
/*
@function: void slist_showAll(const NODE* head);
@berif: 遍历链表数据
@argument: head: 指向头指针变量
@return : 无
*/
void slist_showAll(const NODE *head)
{
  const NODE *p = head;
  while (p)
  {
    printf("%d ", p->data);
    p = p->next;
  }
  printf("\n");
}

/*
@function: int slist_delete(NODE** head,DATA data);
@berif: 删除链表中节点值为data的节点
@argument: head: 指向头指针变量的地址
data: 删除节点中的数据
@return : 成功返回 0
失败返回 -1
*/
int slist_delete(NODE **head, DATA data)
{
  NODE *p = *head, *q = NULL;
  if (!p)
    return -1;
  if (memcmp(&(p->data), &data, sizeof(DATA)) == 0)
  {
    *head = p->next;
    free(p);
    return 0;
  }
  while (p)
  {
    if (memcmp(&(p->data), &data, sizeof(DATA)) == 0)
    {
      q->next = p->next;
      free(p);
      return 0;
    }
    q = p;
    p = p->next;
  }
  return -1;
}
/*
@function: void slist_destroy(NODE** head);
@berif: 回收链表
@argument: head: 指向头指针变量的地址
@return : 无
*/
void slist_destroy(NODE **head)
{
  NODE *p = *head, *q = NULL;
  while (p)
  {
    q = p;
    p = p->next;
    free(q);
  }
  *head = NULL;
}
  • main.c 
    #include "singleList.h"
int main(void)
{
  NODE *head = NULL;
  if (slist_create(&head, 888) < 0)
  {
    puts("create failed");
    return -1;
  }
  slist_addTail(&head, 999);
  slist_addTail(&head, 222);
  slist_addTail(&head, 666);
  slist_addTail(&head, 777);
  slist_addHead(&head, 555);
  slist_insert(&head, 888, 1024);
  slist_showAll(head);
  DATA data;
  while (0)
  {
#ifdef DELETE
    printf("请输入要删除的数据:");
    scanf("%d", &data);
    if (data == -1)
      break;
    if (slist_delete(&head, data) < 0)
    {
      puts("删除失败,请重试");
      continue;
    }
    slist_showAll(head);
#else
    NODE *pFind = NULL;
    DATA newdata = 512;
    printf("请输入要查找的数据:");
    scanf("%d", &data);
    if (data == -1)
      break;
    // if(!(pFind = slist_find(head,data)))
    if (slist_update(head, data, newdata) == -1)
    {
      puts("查找的数据不存在,请重试");
      continue;
    }
    // printf("查找数据:%d 内存地址:%p\n",pFind -> data, &(pFind -> data));
    slist_showAll(head);
#endif
  }
  slist_destroy(&head);
  puts("====销毁后=====");
  slist_showAll(head);
  return 0;
}

「课堂练习2」

创建一个单向表，并从键盘接收数字输入，将输入的正整数按从小到大的顺序插入链表，并
在输入负整数的时候将其绝对值数据删除。每次输入后，将链表的内容打印到屏幕上。

                                                

解析：
此题考查单链表的基本思路，体会链式存储中对于插入和删除的便利性。


参考代码：

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>

typedef struct node
{
  int num;
  struct node *next;
} listnode, *linklist;
bool init_list(linklist *phead)
{
  *phead = (linklist)malloc(sizeof(listnode));
  if (*phead == NULL)
    return false;
  (*phead)->next = NULL;
  return true;
}
bool is_empty(linklist head)
{
  return (head->next == NULL);
}
bool insert(linklist head, int x)
{
  linklist new = (linklist)malloc(sizeof(listnode));
  if (new == NULL)
  {
    perror("malloc failed");
    return false;
  }
  new->num = x;
  /********************************
  the single linklist IS empty
  *********************************/
  if (is_empty(head))
  {
    head->next = new;
    new->next = NULL;
  }
  /*********************************
  the single linklist is NOT empty
  **********************************/
  else
  {
    linklist p, q;
    p = head;
    q = p->next;
    while (q != NULL)
    {
      if (q->num < x)
      {
        q = q->next;
        p = p->next;
        continue;
      }
      break;
    }
    new->next = q;
    p->next = new;
  }
  return true;
}
bool delete(linklist head, int x)
{
  if (is_empty(head))
    return false;
  linklist p, q;
  p = head;
  q = p->next;
  while (q != NULL)
  {
    if (q->num != x)
    {
      p = p->next;
      q = q->next;
      continue;
    }
    p->next = q->next;
    free(q);
    return true;
  }
  return false;
}
void show(linklist head)
{
  if (is_empty(head))
    return;
  linklist p = head->next;
  while (p != NULL && p->next != NULL)
  {
    printf("%d-->", p->num);
    p = p->next;
  }
  printf("%d\n", p->num);
}
int main(void)
{
  linklist head;
  init_list(&head);
  int tmp, ret;
  while (1)
  {
    ret = scanf("%d", &tmp);
    if (ret != 1)
      exit(0);
    if (tmp >= 0)
    {
      if (!insert(head, tmp))
        fprintf(stderr, "insertion falied!\n");
      else
        show(head);
    }
    else
    {
      if (!delete (head, -tmp))
        fprintf(stderr, "%d does NOT exist!\n", -tmp);
      else
        show(head);
    }
  }
  fprintf(stderr, "Bye-Bye!\n");
  return 0;
}

5.9 链表优缺点

链式存储中，所有节点的存储位置是随机的，他们之间的逻辑关系用指针来确定，跟物理存
储位置无关，因此从上述示例代码可以很清楚看到，增删数据都非常迅速，不需要移动任何
数据。另外，又由于位置与逻辑关系无关，因此也无法直接访问某一个指定的节点，只能从
头到尾按遍历的方式一个个找到想要的节点。简单讲，链式存储的优缺点跟顺序存储几乎是相对的。

总结其特点如下：
 
  • 优点
     
    1. 插入、删除时只需要调整几个指针，无需移动任何数据
     
    2. 当数据节点数量较多时，无需一整片较大的连续内存空间，可以灵活利用离散的内存
     
    3. 当数据节点数量变化剧烈时，内存的释放和分配灵活，速度快
     
  • 缺点
     
    1. 在节点中，需要多余的指针来记录节点之间的关联。
     
    2. 所有数据都是随机存储的，不支持立即访问任意一个随机数据。

5.10 循环链表【扩展】

所谓的循环，指得是将链表末尾节点循环地指向链表表头。比如，单向链表变成循环链表的
示意图如下所示：
循环链表的操作跟普通链表操作基本上是一致的，只要针对循环特性稍作修改即可。比如： 
#include <stdio.h>
#include <stdlib.h>
#include <unistd.h>
#include <string.h>
#include <stdbool.h>
typedef struct node
{
  // 以整型数据为例
  int data;
  // 指向相邻的下一个节点的指针
  struct node *next;
} node;
// 初始化一个空的带头节点的循环连表
node *initList()
{
  node *head = malloc(sizeof(node));
  if (head != NULL)
  {
    head->next = head;
  }
  return head;
}
// 创建一个新节点
node *newNode(int data)
{
  // 分配一个新节点的内存
  node *new = malloc(sizeof(node));
  if (new != NULL)
  {
    new->data = data;
    new->next = new;
  }
  return new;
}
// 插入链表的头部
void insertHead(node *head, node *new)
{
  // a.
  new->next = head->next;
  // b.
  head->next = new;
}
// 判断链表是否为空
bool isEmpty(node *head)
{
  return head->next == head;
}
// 遍历链表
void show(node *head)
{
  if (isEmpty(head))
    return;
  for (node *p = head->next; p != head; p = p->next) // 这里不能是p++，不是有序的
  {
    printf("%d\t", p->data);
  }
  printf("\n");
}
// 将链表首部节点剔除
node *removeNode(node *head, int data)
{
  node *tmp, *p;
  for (p = head, tmp = p->next; tmp != head; p = p->next, tmp = tmp->next)
  {
    // 找到要删除的节点的上一个节点指针
    if (tmp->data == data)
    {
      p->next = tmp->next;
      tmp->next = tmp; // 解除引用
      return tmp;
    }
  }
  return NULL;
}
// 销毁链表
node *destroy(node *head)
{
  while (head->next != head)
  {
    node *tmp = head->next;
    head->next = tmp->next;
    free(tmp);
  }
  return NULL;
}
int main()
{
  // 初始化一个空链表
  node *head = initList();
  // 插入一些数据都链表的头部
  for (int i = 1; i <= 5; i++)
  {
    // 1. 创建新节点
    node *new = newNode(i);
    // 2. 将新节点置入链表
    insertHead(head, new);
  }
  // 遍历链表，输出各元素
  show(head);
  // 输入您要删除的节点
  int n;
  printf("输入您要删除的节点：\n");
  while (true)
  {
    scanf("%d", &n);
    if (n == 0)
    {
      break; // 测试销毁，先退出循环
    }
    node *p = removeNode(head, n);
    if (p == NULL)
    {
      printf("没有您要删除的节点！\n");
      continue;
    }
    free(p);
    show(head);
  }
  // 销毁链表，销毁之后返回NULL，此时这个链表就不能在用了
  head = destroy(head);
}

面试题：

对于一个具有 n 和节点的单向链表 (n > 100) ， 只通过一次遍历找到倒数第 50
个节点
提示： 借助于 2个指针，一个在前，一个在后。
 
思路：
 
        先让前一个指针遍历到第50个节点的位置，然后后一个指针，再跟随前一个指针一
起向后移动，当前一个指针遍历完所有节点，后一个指针就是指向了倒数第50个节点的
位置。

嵌入式学习小白ing
关注
数据结构 Day 3 主函数
06-12
main.c
创建一个顺序表，并从键盘接收数字输入，将输入的正整数按从小到大的顺序插入顺序表，并在输入负整数的时候将其绝对值数据删除。每次输入后，将顺序表的内容打印到屏幕上。
qq_65024547的博客
07-31 513
【代码】创建一个顺序表，并从键盘接收数字输入，将输入的正整数按从小到大的顺序插入顺序表，并在输入负整数的时候将其绝对值数据删除。每次输入后，将顺序表的内容打印到屏幕上。
第1章 顺序表和单链表
m0_74916669的博客
08-26 1319
顺序存储中，由于逻辑关系是用物理位置来表达的，因此从上述示例代码可以很清楚看到，增删数据 都非常困难，需要成片地移动数据。顺序表对数据节点的增删操作是很不友好的。总结其特点如下：优点1. 不需要多余的信息来记录数据间的关系，存储密度高2. 所有数据顺序存储在一片连续的内存中，支持立即访问任意一个随机数据，比如上述顺序表中第 个节点是 s->data[i]缺点1. 插入、删除时需要保持数据的物理位置反映其逻辑关系，一般需要成片移动数据2. 当数据节点数量较多时，需要一整片较大的连续内存空间。
顺序表和链表【数据结构】【基于C语言实现】【一站式速通】
2301_79241364的博客
01-23 1560
本文详细介绍了单向链表，双向链表的实现，深入分析了各种数据结构的优缺点，剖析了它们的演变过程，通俗易懂，万字总结，小白无痛学习，同时也欢迎大牛的指导~
顺序表的建立及基本操作
gets_s的博客
02-29 5352
实验内容 1、建立一个顺序表，输入n个元素并输出； 2、查找线性表中的最大元素并输出； 3、在线性表的第i个元素前插入一个正整数x； 4、删除线性表中的第j个元素； 5、将线性表中的元素按升序排列； 6、将线性表中的元素就地逆序（只允许用一个暂存单元）； #include<stdio.h> #include<iostream> #define MAXSIZE 100 usi...
数据结构——顺序表的C语言实现
Winters_coming的博客
10-27 4091
郫县电子专科学院的在读大二，再次保存代码供参考及批评指正 ex1_1——基本题： 1）首先创建一个顺序表：从键盘读入一组整数（长度小于等于20），按输入顺序放入顺序表，输入以－1结束（注意－1不放到顺序表内）；将创建好的顺序表元素依次输出到屏幕上。 2）在已创建好的顺序表中插入一个元素：从键盘读入需插入的元素值和插入位置，调用插入函数完成插入操作；然后将顺序表元素依次输出到屏幕上。 3）在...
数据结构 Day 3 预处理
06-12
head.h
12.20 day1 数据结构
12-20
12.20 day1 数据结构
数据结构day4思维导图
11-25
数据结构day4思维导图
数据结构 Day 3 功能函数
06-12
function.c
顺序表的建立、插入、删除、查找
热门推荐
xiahuayong的博客
04-03 1万+
实验1.1顺序表的建立 1.建立含有N个元素的顺序表并输出该表各元素的值。元素的个数及元素的值由键盘输入，元素类型为整型。 2.实验要点及说明 参考程序中首先调用初始化函数InitList_Seq动态分配顺序表的存储空间，如图所示。顺序表L的长度length是表中所含元素的个数，初始值为0。Listsize是当前已分配的存储空间的容量，是以元素大小为单位的。 建立一个头文件SeqList.h，避免在后面的.c程序中代码冗余。.h文件一般包括程序中必须用到的系统包含文件的声明、常量定义、结构定义及线性表的初始
数据结构顺序表（C语言实现）
Sveinn的博客
04-14 432
数据结构顺序表（C语言实现） 头文件和函数申明 #include <stdio.h> #include <malloc.h> #include <stdlib.h> typedef struct Arr //定义了一个数据类型，该数据类型的名字叫做struct Arr,该数据类型含有三个成员PBase,len,cnt { int *pBase;//储存的是数组...
＜数据结构＞创建一个顺序表
m0_51404980的博客
09-29 3182
实现对顺序表的基本操作 内容：实现顺序表的初始化，输出顺序表中各元素的值，在顺序表中插入数据元素，删除数据元素，求顺序表的长度，顺序表的逆置，顺序表的按值从小到大排序，合并有序的两个顺序表等操作。 同时： （1）要有能根据用户输入选择不同运算的菜单选择界面。 （2）顺序表中数据元素的类型统一抽象表示为ElemType类型，具体类型不限，可以是整型、实型、字符型、或者是自己构造的一种结构体类型。 代码如下，采用分文件编写： List.h #pragma once #include<iostream&gt
实验二：顺序表的实现
grapes1234的博客
10-10 777
一、实验目的 建立一个由n个学生成绩的顺序表，n的大小由自己确定，每一个学生的成绩信息由自己确定，实现数据的对表进行插入、删除、查找等操作。分别输出结果。 二、实验过程 #ifndef SeqList_H #define SeqList_H const int Maxsize=24; class SeqList { public: SeqList(){length=
如何实现一个既保证顺序又有快速插入删除的数据结构？
weixin_44617651的博客
11-13 628
当我们要实现一个既保证顺序又支持快速插入和删除的自定义数据结构，可以考虑使用 双向链表 或 跳表，甚至是结合 字典 和 链表 的方法，这些数据结构在不同需求场景下能够提供优化的性能。
华为OD机试真题---数组二叉树
风信子的博客
11-13 1107
二叉树只也可以用数组来存储，给定一个数组，树的根节点的值储存在下标1，对于储存在下标n的节点，他的左子节点和右子节点分别储存在下标2n和2n+1，并且我们用-1代表一个节点为空，给定一个数组存储的二叉树，试求从根节点到最小的 叶子节点只的路径，路径由节点的值组成。
排序算法 -计数排序
最新发布
qq_46538985的博客
11-16 587
计数排序
数据结构大致分类
weixin_44512485的博客
11-13 688
表、树、图和集合是数据结构的四大基石，每种结构都有特定的应用场景和优势。在实际应用中，选择合适的数据结构对算法的效率和程序的性能至关重要。
数据结构——AVL树
未知陨落的博客
11-16 1459
二叉搜索树虽可以缩短查找的效率，但如果数据有序或接近有序二叉搜索树将退化为单支树，查 找元素相当于在顺序表中搜索元素，效率低下。因此，两位俄罗斯的数学家G.M.Adelson-Velskii 和E.M.Landis在1962年 发明了一种解决上述问题的方法：当向二叉搜索树中插入新结点后，如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整)，即可降低树的高度，从而减少平均搜索长度
数据结构C语言day
08-27
- *1* *2* *3* [数据结构-C语言代码 day 5-多项式加法](https://blog.csdn.net/yydslty/article/details/124612624)[target="_blank" data-report-click={"spm":"1018.2226.3001.9630","extra":{"utm_source":"vip_...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值