蓝桥杯：虚拟迷宫的彩色寻路

问题描述

在一款名为《虚拟迷宫》的游戏中，玩家小然需要在一个N行M列的空白网格地图上寻找宝藏。每个格子都可以被小然用红色或绿色涂满，形成一片五彩斑斓的迷宫。小然定义“有效路径”为从格子(1,1) 开始，到达格子(N,M) 结束的路径，而在移动过程中，他每次只能向右或向下移动一格。对于特定的彩色网格地图，小然将其分数定义为有效路径中红色格子和绿色格子数量相等的路径的数量。你的任务是找出所有可能的N行M列的彩色网格地图的分数之和。由于答案可能很大，输出结果需要对 998244353998244353 取模。

输入格式

第一行输入一个整数T，表示测试用例的数量。

每个测试用例包含两个整数N和M，表示网格地图的行数和列数。

输出格式

对于每个测试用例，输出所有可能的N行M列的彩色网格地图的分数之和，结果对 998244353998244353 取模。

样例输入

3
1 1
1 2
2 3

样例输出

0
2
72

解题思路

        先分析题目意思，对于一个N*M的迷宫，可以在它的上面用红色或绿色填满每一个方格，要我们找出对于不同的填涂方式得到的不同迷宫，找出从走上角的方格位置走到右下角的方格的不同路径数的和，并且要满足路径上的两种颜色的方格数量要是相等的。这里面就要考虑两个三个点，第一个是不同有多少种不同的填涂方式，第二个就是从左上角走到右下角有多少中路径，第三个就是要满足路径上两钟颜色数量要相等。我们先用下面这个2*3的迷宫为例来分析

      

          首先我们不考虑颜色的填涂，直接找从左上角走到右下角的路径数，对于一个2*3的迷宫，会有以下三种情况：1->2->3->6，1->2->5->6，1->4->5->6，由于在走的过程中，下一步要么是向右走，要么是向下走，并且对于一个2*3的迷宫来说，走过的方格数永远是2+3-1，也就是N+M-1，需要确定的方向数会是走过的方格数减1，也就是N+M-2，并且需要确定的向下走的方向数量会是N，向右的为M-1，也就是说在从左上角的位置走到右下角的位置的过程中，我们走过的总的长度是一定的，总的方向确定数也是一定的，只是要确定在哪个位置转动，这样就可以用排列组合来解决这个问题，存在的路径数就可以表示为C（N+M-2，N-1（或为M-1，两者结果是相等的））。

        看不懂上面方法的也可以使用下面这个方法确定路径数：由于在一个点的位置，它下一步只能向右或向下移动，那么可以理解为经过一个点的路径数他只能由在他左边的点的路径数和在他上面的点的路径数之和来确定，因此可以得到下面这个图，方格内的数字表示经过它的路径数。

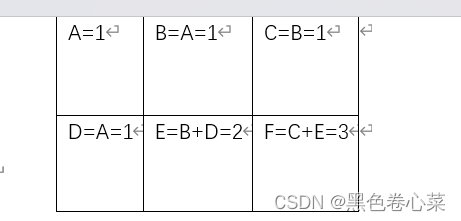
        然后我们需要确定对于不同的填涂方案中有多少种不同的路径，我们分析，对于一种填涂方案，他只有满足某一条路径上的两种颜色数目是相同的时候这条路径才是有效的，这个时候对于这条路径，只有他只有内部颜色数量这一个要求，其他位置的颜色不需要考虑，那对于一条路径它的颜色填涂方案就是N+M-1个方格内确定（N+M-1）/2个方格的颜色为红色或者绿色即可，也就是C  (N+M-1,（N+M-1）/2)，而其他的点的颜色随便填涂这一条路径都满足条件了那么对于这一条路径的情况就有C(N+M-1,（N+M-1）/2)*2**（N*M-(N+M-1)）种满足情况。

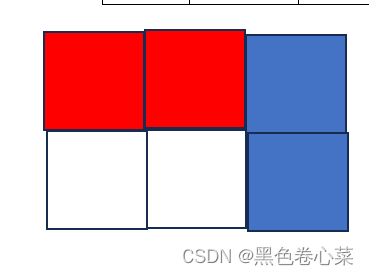
        那么对于C（N+M-2，N-1）种路径他就会有C（N+M-2，N-1）*C(N+M-1,（N+M-1）/2)*2**（N*M-(N+M-1)）种情况，但由于数值过大，在算阶乘的时候需要用定于大数值的模块来定义变量，比如这里的BigInteger。

java解题代码

import java.math.BigInteger;
import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        //在此输入您的代码...
        int n = scan.nextInt();
        int[][] lst = new int[n][2];
        for (int i = 0;i<n;i ++){
            lst[i][0] = scan.nextInt();
            lst[i][1] = scan.nextInt();
        }
        scan.close();
        for (int i = 0;i < n;i ++){
            if ((lst[i][0] + lst[i][1])%2 == 0){
                System.out.println(0);
            }
            else {
                BigInteger b = C(lst[i][0] + lst[i][1]-2,lst[i][0] -1);
                BigInteger a = C(lst[i][0] + lst[i][1]-1,(lst[i][0] + lst[i][1] - 1)/2);
                BigInteger c = BigInteger.valueOf(2).pow(lst[i][0] * lst[i][1] - (lst[i][0] + lst[i][1] - 1));

                System.out.println(a.multiply(b.multiply(c)).remainder(BigInteger.valueOf(998244353)));
            }
        }


    }
    static BigInteger C(int base_number,int index){
        BigInteger val = BigInteger.ONE;
        BigInteger vbl = BigInteger.ONE;
        for (int i = 0;i < index;i ++){
            val = val.multiply(BigInteger.valueOf(base_number - i));
        }
        for (int i = 1;i <= index;i ++){
            vbl = vbl.multiply(BigInteger.valueOf(i));
        }
        return val.divide(vbl);
    }
}