一、什么是二维贪心问题?
二维贪心问题常见于数组排序等操作中,它往往要求所得结果同时满足两个方面的条件,这两个条件相互之间存在某种关联,可以相互影响。如果仅在一个维度上应用贪心算法很容易顾此失彼,难以得出正确答案。
二、二维贪心问题的总体思路
在遇到问题中存在两个维度的要求需要权衡的时候,一定要先确定一个维度,再确定另一个维度。换句话说,也就是要进行两次贪心操作,而且第二次贪心操作是在第一次贪心操作的基础之上进行的。
这种思想和高数中的二重积分颇为相似。
- 第一次积分先解决一个维度(利用贪心思想满足一个维度的要求)
- 后一重积分在积分时既需要满足自己的条件,也需要考虑上一重积分的结果(在第一重贪心的基础上利用贪心思想既满足第二个要求,又不能违背第一重贪心解决的要求)
三、典型例题
(一)根据身高重建队列
题目链接: 406.根据身高重建队列
题目要求:
假设有打乱顺序的一群人站成一个队列,数组 people 表示队列中一些人的属性(不一定按顺序)。每个 people[i] = [hi, ki] 表示第 i 个人的身高为 hi ,前面 正好 有 ki 个身高大于或等于 hi 的人。
请你重新构造并返回输入数组 people 所表示的队列。返回的队列应该格式化为数组 queue ,其中 queue[j] = [hj, kj] 是队列中第 j 个人的属性(queue[0] 是排在队列前面的人)。
提示:
1 <= people.length <= 2000
0 <= hi <= 106
0 <= ki < people.length
题目数据确保队列可以被重建
示例
输入:people = [[7,0],[4,4],[7,1],[5,0],[6,1],[5,2]]
输出:[[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]]
解释:
编号为 0 的人身高为 5 ,没有身高更高或者相同的人排在他前面。
编号为 1 的人身高为 7 ,没有身高更高或者相同的人排在他前面。
编号为 2 的人身高为 5 ,有 2 个身高更高或者相同的人排在他前面,即编号为 0 和 1 的人。
编号为 3 的人身高为 6 ,有 1 个身高更高或者相同的人排在他前面,即编号为 1 的人。
编号为 4 的人身高为 4 ,有 4 个身高更高或者相同的人排在他前面,即编号为 0、1、2、3 的人。
编号为 5 的人身高为 7 ,有 1 个身高更高或者相同的人排在他前面,即编号为 1 的人。
因此 [[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]] 是重新构造后的队列。
解题思路:
首先读题,根据题目和示例可以总结出以下规则:
- 已知队列中每一个人的身高
- 已知队列中每一个人前面身高大于等于这个人的人数
- 所给数据一定有解
- 要求找出原队列的顺序
可以发现,本题是一个较为明显的二维贪心问题,队列中的所有元素必须同时满足身高和前面身高数大于等于这个人的人数两重相对关系。既然如此我们也可以将确定原有队列的步骤分为保证身高更高的人在前面和右侧相对关系正确两部分,当所有除端点以外的所有元素均满足两重相对关系时,所得序列一定是合理的。确定了问题类型和大致思路以后,我们又面临着以下两个问题:
- 一共有两个维度,应该先考虑哪一个?
如果按照k来从小到大排序,排完之后,会发现k的排列并不符合条件,身高也不符合条件,两个维度哪一个都没确定下来。
那么按照身高h来排序呢,身高一定是从大到小排(身高相同的话则k小的站前面),让高个子在前面。
此时我们可以确定一个维度了,就是身高,前面的节点一定都比本节点高!——《代码随想录》
- 身高这个维度到底贪什么?
问题本身并没有对身高做出明确的要求,那么身高这个维度的贪心目的应当是为另一维度的贪心操作提供便利,根据问题可知,另一重贪心注重研究k(每一个人前的身高高于该人的人数)。具体来说,身高低的人是不会对身高高的人的排序(k)造成影响的,所以先把身高高的人排序好了以后,无论低身高的人怎么排都不会造成身高高的人的位置错误,所以只要每次确定好身高较高的人的相对位置,再将低身高的人插入就是正确的排列。因此将队列中身高更高的人排在前面更有利于后续通过遍历先排身高更高的人,因为此时只需顺序遍历队列,根据k的值将元素依次插入队列中即可。
首先需要对二维数组people[][]进行排序,可以利用标准库中的sort函数进行排序,排序的规则如下:
- 两个元素之间相互比较,身高h更高的排在前面
- 如果两个元素的身高相同,则比较两者k的值,k值更小的排在前面,因为k表示该元素前还有多少个身高大于等于h的元素数,所以k越小,说明前面的元素越少,应该排在更靠前的位置。
static bool cmp(const vector<int>& a, const vector<int>& b) {
// 定义第一个维度的贪心规则
// 如果身高相等,k更小的元素排在前面
if (a[0] == b[0]) return a[1] < b[1];
// 身高更高的排在前面
return a[0] > b[0];
}
sort (people.begin(), people.end(), cmp);
接下来我们需要进行第二重贪心。之所以要进行第二重贪心,是因为在第一重贪心中,我们只关注了身高的因素,导致当前队列中身高更高的一定排在前面,但事实上,原队列中也可能有身高较低的人排在身高较高的人前面的情况,这次贪心我们就需要保证所有的k均与队列中元素的相对位置关系相匹配。由于第一次贪心操作确保本轮操作一定是先操作身高更高的人,所以后插入的元素(身高较低,不计入k)一定不会干扰之前插入的元素相对位置的正确性。所以只需要将每一个元素直接按照k的值插入即可。
注意本次操作需要使用insert()库函数,这个函数可以将某一个值插入数组指定下标处,原有的元素将会顺延。
#include <iostream>
#include <vector>
using namespace std;
int main() {
vector<int> vec = {1, 2, 3, 4};
vec.insert(vec.begin(), 10); // vec = {10, 1, 2, 3, 4}
vec.insert(vec.begin() + 2, 11); // vec = {10, 1, 11, 2, 3, 4}
}
vector<vector<int>> que;
for (int i = 0; i < people.size(); i++) {
int position = people[i][1];
que.insert(que.begin() + position, people[i]);
}
代码示例:
class Solution {
public:
static bool cmp(const vector<int>& a, const vector<int>& b) {
// 定义第一个维度的贪心规则
// 如果身高相等,k更小的元素排在前面
if (a[0] == b[0]) return a[1] < b[1];
// 身高更高的排在前面
return a[0] > b[0];
}
vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
// 第一轮贪心排序
sort (people.begin(), people.end(), cmp);
// 第二轮贪心排序
vector<vector<int>> que;
for (int i = 0; i < people.size(); i++) {
int position = people[i][1];
que.insert(que.begin() + position, people[i]);
}
return que;
}
};
(二)、分发糖果
题目链接: 135.分发糖果
题目要求:
n 个孩子站成一排。给你一个整数数组 ratings 表示每个孩子的评分。
你需要按照以下要求,给这些孩子分发糖果:
每个孩子至少分配到 1 个糖果。
相邻两个孩子评分更高的孩子会获得更多的糖果。
请你给每个孩子分发糖果,计算并返回需要准备的最少糖果数目 。
提示:
n == ratings.length
1 <= n <= 2 * 104
0 <= ratings[i] <= 2 * 104
示例
输入:ratings = [1,2,2]
输出:4
解释:你可以分别给第一个、第二个、第三个孩子分发 1、2、1 颗糖果。第三个孩子只得到 1 颗糖果,这满足题面中的两个条件。
解题思路:
首先读题,根据题目和示例可以总结出以下规则:
- 每个孩子至少分配1个糖果
- 相邻孩子中评分更高的孩子一定比评分低的孩子有更多糖果
- 相邻孩子的评分如果相同,所得到的糖果数可以不相同(例如对评分 [1, 2, 2, 3], 糖果总数最少的情况为 [1, 2, 1, 2]
- 要求找出最少所需的糖果总数
读题以后发现简单地遍历数组,看到后一个元素更大就加一,更小就减一的方法显然是不行的,因为这种方法将视野限制在当前的两个元素上,如果出现连续递减的情况,则糖果数很有可能小于1。为了解决这个问题,我们可以将视野扩展的局部区间,寻找最长连续递增(递减)子序列,子区间左端(右端)端点的糖果数一定是1,其余节点糖果数依次递增(递减)1。但这种思路只考虑到了某一个单调区间的取值问题,无法处理其余部分的取值,详细地说就是递增区间右侧的第一个元素的取值既不能简单地通过减一得到(它有可能比周围的元素都小,可以取0),也不能直接赋值为0(它有可能大于右侧的元素,必须比右侧元素大1)。
事实上,根据分析可以发现,糖果数序列中除端点以外的所有元素必须满足左右两重相对关系。既然如此我们也可以将确定糖果数的步骤分为保证左侧相对关系正确和右侧相对关系正确两部分,当所有除端点以外的所有元素均满足两重相对关系时,所得序列一定是合理的。这两个过程均可以通过一重for循环遍历数组来实现。
首先初始化糖果数数组nums[]中的每一个元素为1,以免出现最小糖果数小于1的情况。
然后保证右半部分的关系正确:
从前向后循环,保证如果右侧评分大于左侧评分,则右侧孩子糖果数一定更多
for(int i = 1; i < ratings.size(); i++) {
if(ratings[i] > ratings[i-1]) nums[i] = nums[i-1] + 1;
}
保证左半关系同时正确:
注意本次遍历所确定的元素的是比较的元素对中右侧的nums[i+1],所以每一次比较都要保证右侧的元素已经比较过了,为保证这一点我们必须从右向左遍历数组。
注意:
- nums[i] + 1 是 nums[i+1] 满足左侧条件的下限
- nums[i+1] 是 nums[i+1] 满足右侧关系的下限
- 两个下限必须同时满足,所以取两者最大值
for(int i = ratings.size() - 2; i > -1; i++) {
if(ratings[i+1] > ratings[i]) {
nums[i+1] = max(nums[i] + 1, nums[i+1]);
}
}
代码示例:
class Solution {
public:
int candy(vector<int>& ratings) {
int ans = 0;
vector<int> nums(ratings.size(), 1);
// 第一次从前向后循环,保证如果右侧评分大于左侧评分,则右侧孩子糖果数一定更多(保证了右半部分的大小关系正确)
for(int i = 1; i < ratings.size(); i++) {
if(ratings[i] > ratings[i-1]) nums[i] = nums[i-1] + 1;
}
// 第二次从后往前循环,保证如果左侧评分大于右侧评分,则左侧孩子糖果数一定更多
for(int i = ratings.size() - 2; i > -1; i--) {
if(ratings[i] > ratings[i+1]) {
// nums[i] + 1 是 nums[i+1] 满足左侧条件的下限
// nums[i+1] 是 nums[i+1] 满足右侧关系的下限
// 两个下限必须同时满足,所以取两者最大值
nums[i] = max(nums[i], nums[i+1] + 1);
}
}
// 计算糖果总数
for(int i = 0; i < nums.size(); i++) {
ans += nums[i];
}
return ans;
}
};
nums[i], nums[i+1] + 1);
}
}
// 计算糖果总数
for(int i = 0; i < nums.size(); i++) {
ans += nums[i];
}
return ans;
}
};







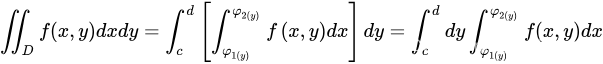













 1937
1937











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








