记录遇见的错题
不能断定x和y是否为正数 所以需要加绝对值
不过不用担心,也等于1/x(记住这个结论)

———————————————————————————————————————————
算极限的时候,不能局部等价无穷小和局部带入, 简单点讲就是精度太低,
就是下面这两种方式都是错的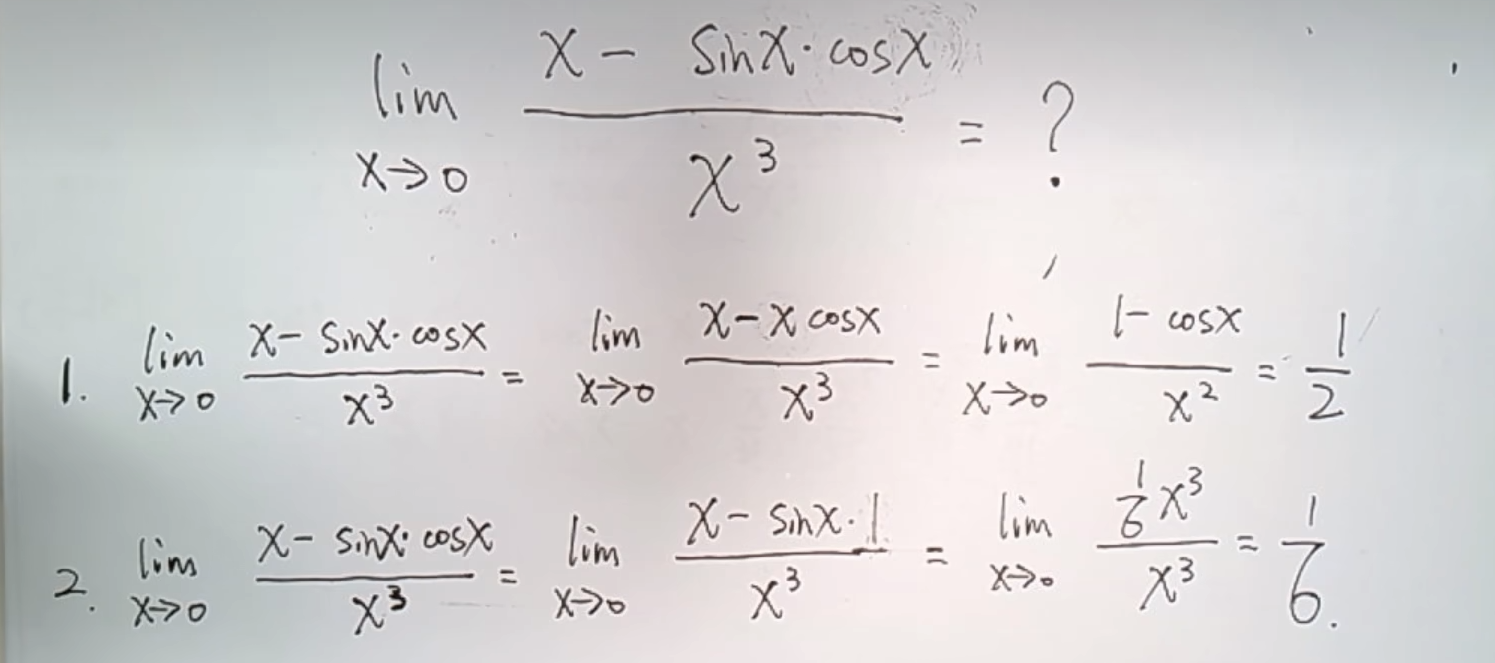
下面是上述的补充
无穷小阶的运算
一.加法替换的规则:
1.若替换后的x同阶
则必须要求替换后x的系数相加不等于0
比如下面这个
2.若是替换后x不同阶 比如下面这个
比如下面这个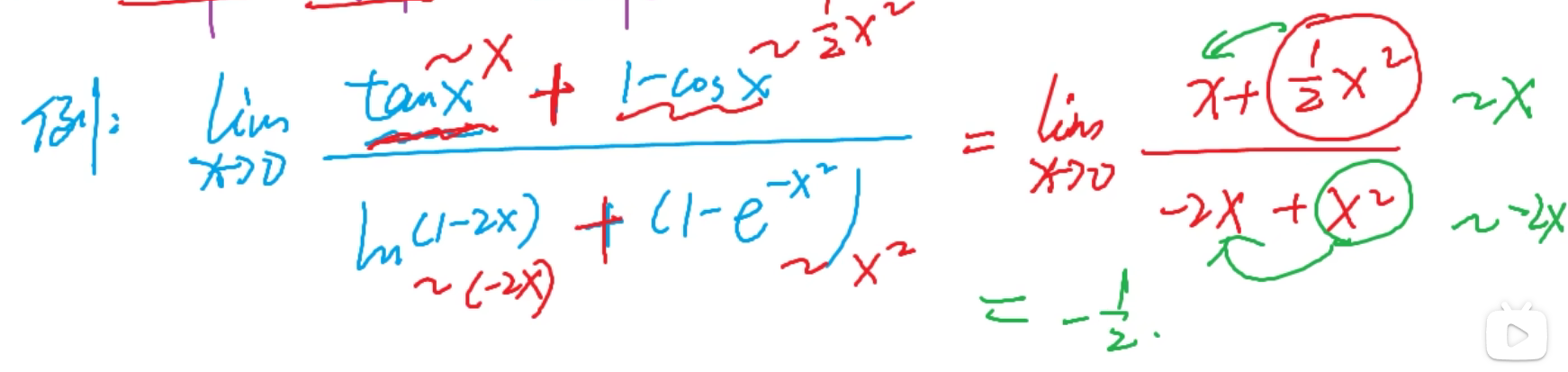
3.lim可以等于
(x代表含未知量的式子,我只想表达极限可以提到幂上边)
二. 这是几个无穷小量的运算公式 m n代表阶数
———————————————————————————————————————————
因为三角函数有如下等诸多变换,所以写三角函数题可以考虑添项减项


和差化积
常看常新


极限
定积分计算极限
下面黑色字是例题

下面是较复杂一点的情况
变元就相当于
由题意得,k是从1开始,直到n;所以k的范围是1到n;这样就可以推出的范围了
但是注意,只有单纯的的话(上面的情况)积分范围就是0到1,不要用下面的方法算
步长就相当于变元的前一项减后一项。也就是
补充理解:
下图左右式子相等的原因:
相当于把0到1上函数围成的面积切成n份矩形,那么每一份矩形的底就是,长就是对应的函数值
举个例子,针对第k个矩形。当x=时矩形的高就等于f(
),底就等于
=

续:这样子函数与x轴围城的面积就可以由左式表示,同时右式为定积分,也能表示在0到1上函数的面积,故下式相等
同理,当积分区间是(0,2)时,把面积分为n份,每一份的步长就是,第k个矩形的高度就是

两个东西是等价无穷大,取指数不一定还是等价无穷大
取e会把两个数之间的差距拉大,取ln会把两个数的差距拉小。所以算两个数之间是否存在等价无穷大(小)的时候不能取对(指数)
比如n和明显不等价,但是lnn等价于ln
遇到不会的题 可以考虑一下统一形式
比如这里就是为了统一在减号后边的项乘了个
记住:

推导过程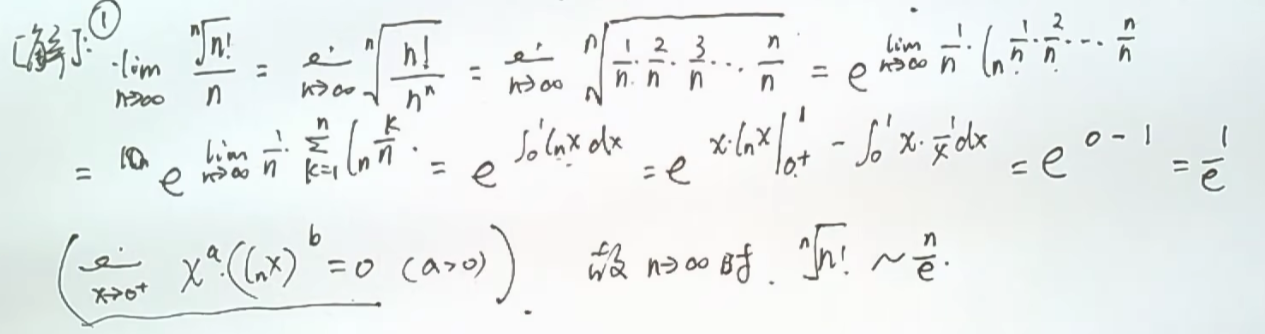
抓大头思想↓
抓大头原理:就是把最高次数的项除下去
注意:=|x|,不注意的话会错,而且必须是乘除形式
 总结:
总结:


而且要注意求极限的两边;他们相等极限才存在

定义题
就是问下面这种问题
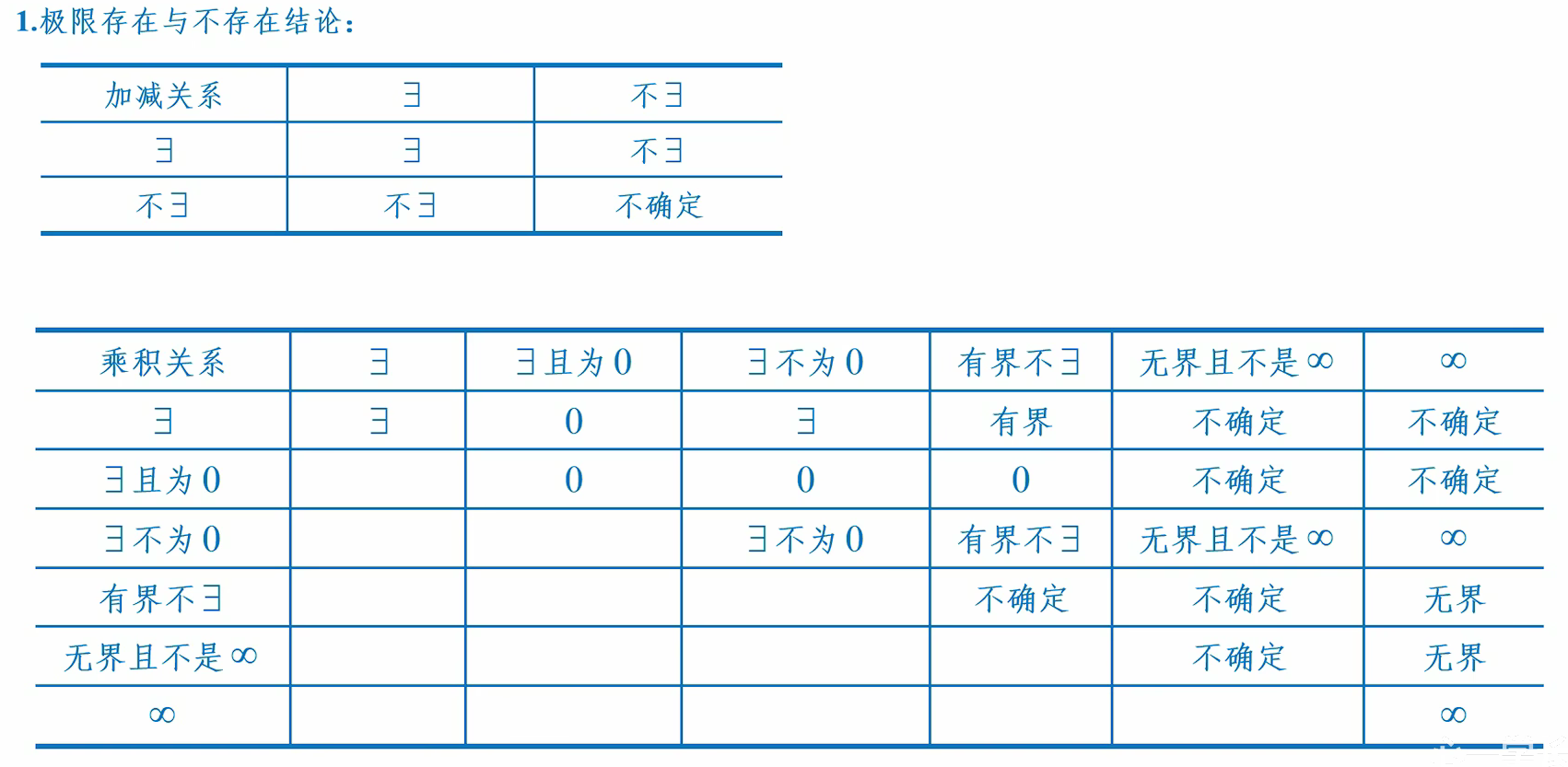

无界和无穷大的区别

化简如下面这样的式子
结论:积分下限为0的时候,把积分上限和被积函数等价无穷小,这样一通操作后的函数就是原函数的等价无穷小

高阶导数及其间断点~拉格朗日中值定理
利用拉格朗日定理(这里以1.50为例子)
(拉格朗日中值定理中
的范围)
因为n趋于无穷时n-1/n和n/n都等于1,所以等价于n
最后把=n替换进
就可以了

记住下面这个重要变换


记住下面这个重要结论

-1到0和0到+1之间的函数表达式都是1+x
当x趋于-1的右极限,limf(x)=(1+x)等于0, 由图 趋于-1的左极限时f(x)=0,此时函数左右极限相等 故取x=-1时f(x)存在极限
同理,当x趋于1的左极限时,f(x)等于2

要求连续,就要有x->0时;但因为是分段函数,所以需要分成从0的两边逼近来分类讨论
(?)
求高阶导数 可以用
1.图中公式法
2.泰勒
3.求一二阶归纳规律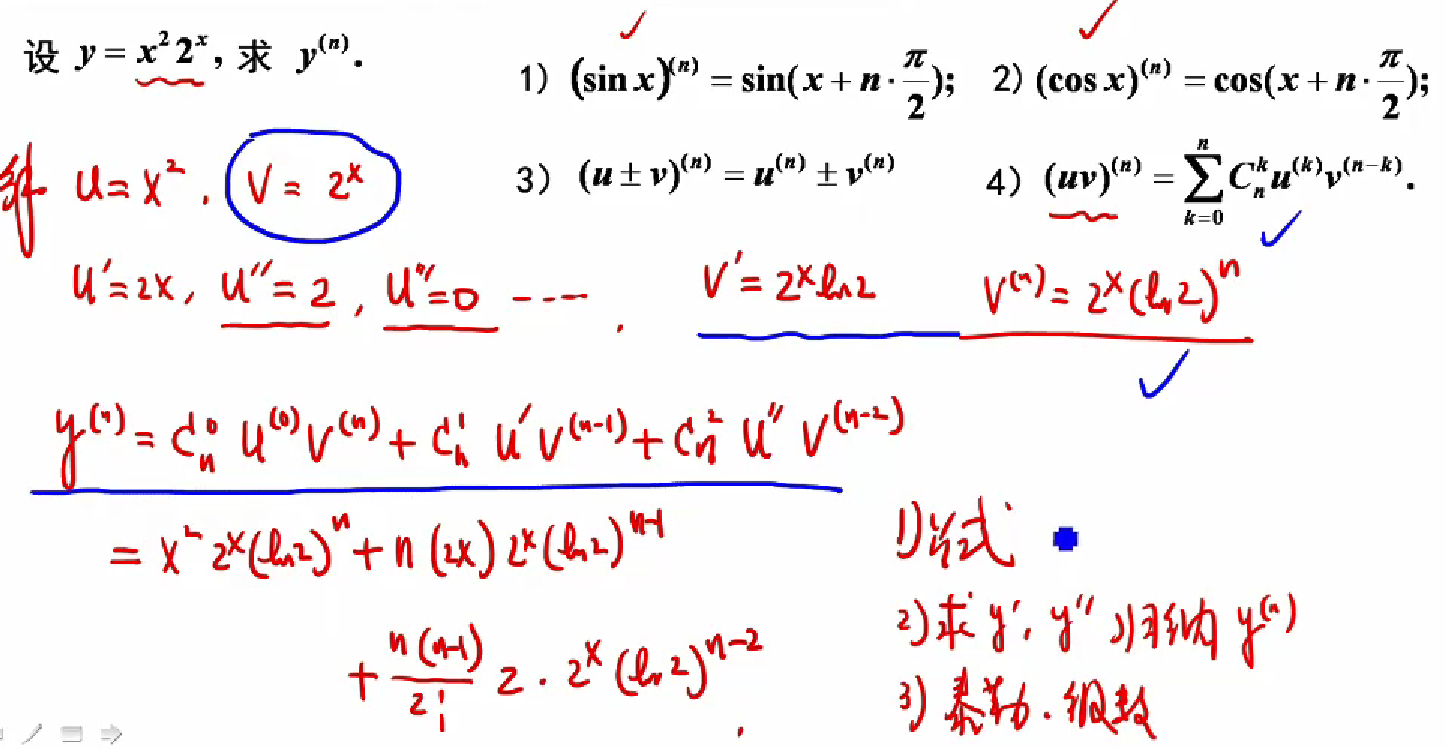
换元法:
把x-1换成t,这样就可以把变量设置成趋于0
x+2可以直接带入x趋于1,算出等于3

当遇见选择题的时候,可以选择:
1.构造函数法——构造一个符合题目且简单的函数
2.带数运算——把数字带进题目,看符合哪个选项
这种方法只能排除 不能直接选
a f(x)=x^3符合单调增,但是导函数存在为0的点
b 当x=-x时令g(x)等于f(-x);求导有=
在原函数发生变化时用一个新函数表示,这样会比较明显 ,不然就会误认为<=0(实际应当是
<=0)

可以化成红笔部分的形式;
因为(x-a)^n的n为大于1的整数,所以(x-a)/(x-a)^n趋于无穷
要相乘等于-1,只能是等于0【1】
要判断极值,除了=0,还需要左右两侧的导函数变号
这就用到保号性 因为原式等于-1,也就是小于0 然后参考蓝字就可以分析出D

补充;【1】如果是相除为0,说明分母是分子的高阶无穷大

实际上是二阶导的公式
一阶导为0,二阶导为负数 该点取得极大值 这是书上公式

判断是否存在高阶导数
这里为了判断拐点是否存在,用到了三阶导数
但是在用三阶导数前,要先判断函数是否存在三阶导
原式可以变化为蓝色部分
因为x可导,而函数存在二阶导,所以一阶导也可导。因为等式右边都可导,故左边也可导。所以函数二阶可导,即存在三阶

确定渐近线要分三种情况讨论:水平,垂直,斜渐近线
有水平渐进线,就没有斜渐近线了
水平渐近线是x趋于无穷时y趋于某个特定的数,这里y趋于无穷,故无水平渐近线
垂直渐近线是x趋于分母为0的点时,函数趋于无穷 这里也无垂直渐近线
斜渐进线求的步骤就是如下图所示了,结果是y=x+1/e

或者也可以用解法2:
先把原式变成这样,后面那一项当x趋于无穷时趋于1/e
我们需要把原式变成ax+b+o(x)的形式(当x趋于无穷时,o(x)趋于0)
 所以我们再变换成下面这样,就完成了
所以我们再变换成下面这样,就完成了
证明函数的零点问题可用罗尔定理 就是把函数反向求导求得“原函数”

单中值一般构造辅助函数用罗尔定理 双中值用柯西和拉格朗日中值
逆用罗尔定理




中值定理辅助函数
辅助函数使用举例 改写成相减的形式
改写成相减的形式
推广的积分中值定理()

中值定理题中出现的形式 ,就考虑构造
的辅助函数
这里主要是因为求导后还是
,联想到在等式两边同时乘
下面的同理

积分
不定积分
积分的题,一定记住:函数里含参数太复杂,一定要记得考虑换元
令的值为I,最后算得
,把
的值为1代入等式

有根号换元法典型情况:
根号里是:
1.一次函数
2.一次函数除一次函数(下题,而且要注意换元后并不是单纯的dx=dt)
3.指数函数
4.指数函数除指数函数
若是根号里是二次函数,最好考虑三角代换
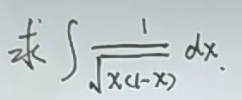

如图 参考思路
记住口诀 反对幂三指
在这个口诀中,谁排到后面,那么分部积分的时候就要把谁凑到d后面

三角换元不一定非要拘泥于1-,也可以尝试下面这种

题:

原式可化为:
实在想不到可以尝试先把式子的一部分代会d后边 看式子剩下的部分有没有什么关联(就是凑微分)
而且记住下面这是的固定化的化简方法

隐函数的不定积分的类型题,方法只有一个,就是找出y=y(t),x=x(t);然后原式就变成了只含有t的式子
将y=tx(这里的t并不是常数,可看作函数)带入原式(即),求出x和t的函数表达式
,同理得出y和t的函数表达式,再把这两个式子代回原式替换x,y

注意:找参数方程时并不一定是y=tx,也可以y+x=t,x=ty;怎么方便怎么来
注意这个东西积不出来

题

答
解
这里可以通过cosnx在0到2上小于1放缩掉,这杨积分式子就不含有cosnx了,就方便求导了

二重积分
记住下面这个变tanx的方法
等式上下同时除,分子1就会变成
,
dx就等于dtanx

在遇见类似于这种题所给的条件,因为不好在直角坐标系里画出来,所以可以使用极坐标

如下,以曲线1为例
曲线1用极坐标表示可表示为r==
因为是第一象限,所以的范围是0到
再根据三角函数周期性,发现当处于0到
时,sin2
递增,r(也就是图像到原点的距离)递减
处于
到
时,sin2
单调递减,r(也就是图像到原点的距离)递增

下面含绝对值的不等式
右式的前提是a<=b,要是a>b结论相反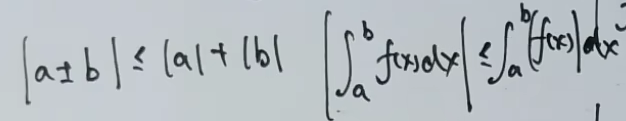

题型:
遇见同名函数加减(比如下面这种),要是中值定理问题可考虑拉格朗日;要是积分问题就考虑二重积分

当然,有可能有的二元函数题用先x后y的次序解题;但在对x积分的时候积的时候积得出,对y积分的时候积不出,就变成了上面这种形式
那么出现上述形式,就要还原成原来的二重积分的样子,然后改变积分的顺序就可以了
看到也就是三角函数乘指数函数这样的式子,就可以连续两次分部积分


连续分部积分后,得到原函数,再解方程
而且最好第一次把什么放进去,之后也要把同类型的放进去
比如第一次放三角函数,第二次也放三角函数
雅可比换元法
要注意用的是雅可比行列式的绝对值

雅可比变换的
例题1.


例题2.
遇见椭圆,可以用雅可比行列式变换为圆
变限积分求导
要求被积函数中不能含有求导变量
要是有,就要想办法把求导变量弄出去
下面是把求导变量弄出去的办法
1.直接把求导变量x移出去
2.利用区间再现去掉求导变量x,记得使用区间再现时t是自变量
3.利用换元法去掉x(记得换元了积分区间也要变)
错题

答案


解析
1.根据原先积分的 上下限,可以画出图(ux轴)

2.z(x,y)=,把
看作f(x),用上面式子的式一

3.计算dz/dx,则是先把无关变量g(xy)提出来,再用式二

错题

答案

解析
1.一般而言,打开绝对值后,要考虑函数变号,所以要考虑积分分段的问题
但因为x-y的范围是到0,这个范围内sinx一直是负的
根据sinx函数的图像,|sin(x-y)|去掉绝对值后,就相当于是sin(y-x)

1.使用区间再现,清除sin(y-x)里的x

2.因为积不出来,所以可以把lnsiny放到
dx里

3.记住公式:
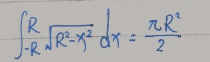
推出:

错题

答案
解析
1.由原式求出r的范围(从小圆到大圆)



2.可以把和r换成x和y,方便理解

然后再用直角坐标交换积分次序就可以了 
错题

答案
解析
1.只解释坐标轴的变换

这里的I1指的是小圆D1,小圆D1是圆心为(,
),半径为1的圆,要对此圆以原点作极坐标,显然不容易算
和r,所以可以把圆心为原点 再建立极坐标系
把在原点的圆看作是以圆心(0,0)为基准,(x-0)=rcos;
就很容易理解以(,
)为基准的圆,是(x-
)=rcos
了

通过乘除添项的方式得出d
反常积分
反常积分可以简单的解释为:一个在积分区间上不好算出来的函数
具体体现是在积分区间是无穷函数,或者在积分区间上的某个(些)点取不到
同时,可以把积分区间上取不到的点称为瑕点,比如下面积分的x=0的点就是瑕点
但是注意有一个坑,就是求反常积分,若在积分区间有瑕点的话,就要把积分从瑕点处拆开
拆开后是这样子。
 从图像上看,似乎
从图像上看,似乎和
能相互抵消

但因为A和B趋于0的速度不一定一致,所以不等于0
这里的同一个极限体系指的是如
不同的极限体系指的是,因为x和y趋近于无穷的速度不同,无法比较

记住:
ps:这里第4点要求0<q<1时必须要确保是反常积分


判断反常积分是否收敛
1.找出瑕点(这里可能是0和1,因为若b<0,当x=1时1-x取不到)
2.当趋近1时,(由于积分范围,只能从左侧趋近),x可等价无穷小为1,lnx可以等价无穷小为1-x
3,记得取收敛范围的时候要在(0,1)内,这样才能确保它是反常积分

伽马函数(超纲)

 由上图可得:
由上图可得:
下面是稍微复杂一点的情况
微分方程
错题

答案

解析
1.这种题一般要两边求导构造微分方程![]()
2.看到这种两个函数自变量不一样(一个是x,一个是-x),用不了什么常系数齐次线性微分方程之类的

要想统一自变量,就要记住三步:
求导 替换 抵消
求导:再导一次,导出二阶
替换:这题里的替换是吧原式用-x替换x
反正记得最后的目的是统一f里的变量
3.因为求了两次导,这里记得要把c1和c2算出来

记住:要先判断是否二阶可导(虽然大概率二阶可导)
因为,0和f(-x)都可导,故
也可导
因为算不了,所以把自变量y用
代替
这样原式就变成,就可以用一阶常系数齐次线性微分方程

三重积分
一重积分是一条线在积分区间的叠加积分,所以几何意义是面积
二重积分是一个面在积分区间的叠加积分,所以几何意义是体积
为什么我要放在这里? 主要是这道题可以体现利用二重积分是面积的方法快速计算(法1)
而且记得是奇函数,积分区间是对称的可以直接消除

无穷级数
级数收敛,说明趋向于0 即
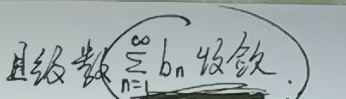
由此,还能推出:当n趋于无穷时,趋于0
再利用等价无穷小可推出,
当趋于0时,

记得在级数问题中考虑等价无穷小
判断敛散性
比值判别法做出来的根值判别法一定做的出,但根值判别法做得出的比值判别法不一定做得出
做不出指的是利用根值判别法,算出an一种情况下有多个极限。这显然是不合理的
众所周知,在根值判别法和比较判别法中,当p=1时方法失效
因此,当p=1时,就要判断当n趋于无穷时是否趋于0.当趋于0时收敛,否则发散
如题,使用根值审敛法,发现最后结果是,p的结果是0
所以第二行是求的极值,发现n趋于无穷时
趋于1,故原级数发散

除了通过求极限,单调性也可以找出当n趋于无穷时是否趋于0
斯特林公式


已知,
.....
,
当n趋于无穷时,都等于0

因此
当n趋于无穷时,ln(n+2)比2大,比n小。因为ln(n+2)夹在2和n之间,所以根据夹逼法,等于1

stolz定理
收敛,不代表
收敛
 所以这里需要把
所以这里需要把从根号里拿出来才能做
p级数的敛散性
比较判别法的极限形式
 例题
例题
结论

下面是lnn的等价无穷大

而且注意下面等式是错误的,两个东西等价无穷大;取指数不一定是等价无穷大
对数判别法(超纲)
可以用在比较判别法和根值判别法都失效的情况下
注意结论和比较判别法,对数判别法是相反的

尤其是用在这种形式的级数上有奇效

例题
求幂级数的和函数
求幂级数的和函数,主要分为三个方法:
1.套用现成公式法(重点)
利用先积后导推到出一些公式
已知的展开式是
,令x=-x,就得出了
的展开式(注意是有
)
对积分,就得到了ln(1-x)的展开式,同理也可得ln(1+x)
将其相加,即可得ln(1-),相减可得ln(1+
)
令x=,即可由
推出
的展开式,对其积分即可得arctanx的展开式



对于右下角三个式子
对 =
等式左右求导,记住求导完后右边应当是n=1而不是n=0。然后再令n+1=n,则
; 即可得到
的展开式
就是对
=
求导两次的结果,记得最后也要令n=n+1

在套用的时候要记得公式形式
要注意随时变换n=0和n=1的式子
而且注意这道题。可以把x提出去。因为自变量是n,x可看作常数。相对应的,n就千万不能提出去
当遇到是的题

通法是构造下面这个函数

用待定系数法列下面这个式子,求解ABC

得出A B C后直接用上式右边代替,带入原式
而且记得这里题目是n=1开始的;公式是n=0开始的,所以需要减去n=0的项
最后因为题目是 ,要把
变成
的形式(最后一步)
主要就是把负一次幂提进2里边,变成
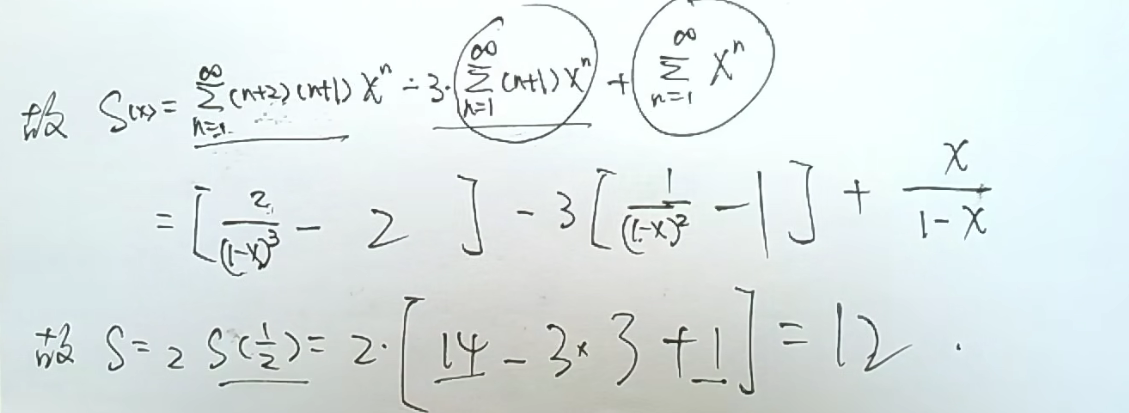
错题
答案(只针对求和函数)

解析
1.遇见这种求和函数的题,立马想到构造微分方程

2.题目只给出这样的等式,要注意等式成立的n的范围(题中并未给n>=1,这里是因为不存在an=0的情况)

这里的就是因为是n=0,不能用题所给的等式,只能把n=0的项单独提出来

3.题给的已知项可以用来算参数
一个拆数的小妙招
上面的式子因为分子含有n+1,要拆只能拆成+
第一个式子含有n用不了sinx的式子
所以可以先提个1/2出来,把分子变成分母样式,这样再拆分就好拆了

这个拆数的方法在其他类型的题目的分式里也很有用
2.构造微分方程
求一次导用不了微分方程就多求几次导
再带入展开式(S(0)=1),可以得出常数项或
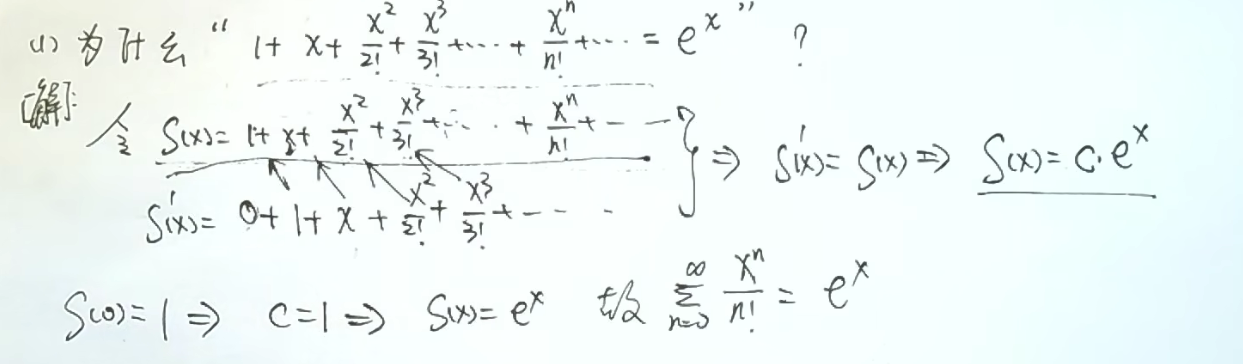
傅里叶级数

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








