机器学习笔记01_为什么方差代价函数要使用平方而不直接使用误差的绝对值？（最全解析）

线性回归模型

线性回归模型被假设为

其中  和 b 被称为模型参数，通过调节合适的  和 b 的大小，可以使得预测值更接近真实数据。

但是  和 b 值的大小，我们可以有很多个选项，那么如何比较不同的  和 b 之间，哪一组预测的输出更接近真实数据呢？

因此，我们引入了代价函数（Cost fuction）

代价函数（Cost fuction）

衡量拟合曲线与训练数据的吻合程度

方差代价函数（Squared error cost fuction）

这是机器学习中普遍使用的一种代价函数，也是通常初学者最先接触的一种代价函数

 =  ：模型的预测值                  ：真实数据

由我们的目标可知，当均方差越小，代表模型预测值越接近真实数据，其拟合效果就越好

回归到数学问题上，也就是说，只需要令方差代价函数的导数为零，求出方差代价函数取最小值时的   和 b，就能得出拟合效果最好的线性回归模型了。

为什么要在方差公式中乘一个  ？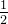

因为我们在求函数的最小值时，需要进行求导操作，乘   可以简化数学运算，与平方求导直接抵消，同时也不会影响方差代价函数所表达的衡量拟合曲线与数据吻合程度的实际意义。

为什么要使用方差而不直接使用误差的绝对值？

定性解释

• 使用绝对值误差的时候，会出现零点不可导问题。这意味着绝对值函数不是光滑的，它在某些情况下可能不具有可微性。

• 需要判断  的正负，这样会导致在计算上的复杂性。

• 平方的方法使得每个数据点和平均值之间的差异都被放大了，而不是简单地抵消掉，对于处理异常值会更加敏感。
• 均方误差的梯度计算比平均绝对误差的计算更加稳定。

数学解释

均方误差的理论基础是假设误差服从高斯分布。也就是说，我们假设预测值的误差服从正态分布

此时，这个误差 可以被假定为：

平均值 u = 0，方差为σ 的正态分布

那么在已知正太分布的情况下，每一个数据点都会对应一个误差，而误差出现的概率，我们可以直接通过正态分布函数求得。

所有数据点误差概率相加，得： 

                                                                  （1）式

对这个函数两边同时求对数，进行极大似然估计：

                                                                    （2）式

补充知识：极大似然估计

极大似然估计可以拆成三个词，分别是“极大”、“似然”、“估计”，分别的意思如下：

极大：最大的概率

似然：看起来是这个样子的

估计：就是这个样子的

极大似然估计就是在只有概率的情况下，忽略低概率事件直接将高概率事件认为是真实事件的思想

因此，极大似然估计的通常求解步骤如下：

1、得到所要求的极大似然估计的概率的范围

2、以概率为自变量，推导出当前已知事件的概率函数式 L

3、求出能使得 L 最大的概率

因此，我们需要求得   的最大值

所以，我们只需保证 （2）式中 等式右边的值最大就可以了

因为（2）式右边的第一项和第二项都是定值，所以只需要求第三项的最小值

由假设前提可知 u = 0，只需要求  最小即可

其中  表示误差值

参考文章：

06_在机器学习中，为什么使用均方误差而不使用绝对值误差-CSDN博客

python 预测平方误差_机器学习第2天：什么是线性回归？为什么是距离的平方不是绝对值...-CSDN博客