4月22日-过拟合与欠拟合、批量标准化

4月22日复盘

2.4.5 Adam

Adam（Adaptive Moment Estimation）算法将动量法和RMSProp的优点结合在一起：

• 动量法：通过一阶动量（即梯度的指数加权平均）来加速收敛，尤其是在有噪声或梯度稀疏的情况下。
• RMSProp：通过二阶动量（即梯度平方的指数加权平均）来调整学习率，使得每个参数的学习率适应其梯度的变化。

Adam过程

1. 初始化：

   • 初始化参数 ${\theta }_0$ 和学习率$\eta$。
   • 初始化一阶动量估计 $m_0=0$ 和二阶动量估计$v_0=0$。
   • 设定动量项的衰减率 ${\beta }_1$ 和二阶动量项的衰减率${\beta }_2$，通常${\beta }_1=0.9$，${\beta }_2=0.999$。
   • 设定一个小常数$ϵ$（通常取$10^{-8}$），用于防止除零错误。

2. 梯度计算：

   • 在每个时间步 $t$，计算损失函数$J(\theta )$ 对参数$\theta$ 的梯度$g_t={\nabla }_{\theta }J({\theta }_t)$。

3. 一阶动量估计（梯度的指数加权平均）：

   • 更新一阶动量估计：
     $$m_t={\beta }_1{m}_{t-1}+(1-{\beta }_1)g_t$$
     其中，$m_t$ 是当前时间步 $t$ 的一阶动量估计，表示梯度的指数加权平均。

4. 二阶动量估计（梯度平方的指数加权平均）：

   • 更新二阶动量估计：
     $$v_t={\beta }_2{v}_{t-1}+(1-{\beta }_2)g_t^2$$
     其中，$v_t$ 是当前时间步 $t$ 的二阶动量估计，表示梯度平方的指数加权平均。

5. 偏差校正：

   由于一阶动量和二阶动量在初始阶段可能会有偏差，以二阶动量为例：

   在计算指数加权移动平均时，初始化 $v_0=0$，那么$v_1=0.999\cdot v_0+0.001\cdot g_1^2$，得到$v_1=0.001\cdot g_1^2$，显然得到的 $v_1$ 会小很多，导致估计的不准确，以此类推：

   根据：$v_2=0.999\cdot v_1+0.001\cdot g_2^2$，把 $v_1$ 带入后，
   得到：$v_2=0.999\cdot 0.001\cdot g_1^2+0.001\cdot g_2^2$，导致 $v_2$ 远小于 $g_1$ 和 $g_2$，所以 $v_2$ 并不能很好的估计出前两次训练的梯度。

   所以这个估计是有偏差的。

   使用以下公式进行偏差校正：
   $$\begin{gathered} {\hat{m}}_t=\frac{m_t}{1-{\beta }_1^t} \\ {\hat{v}}_t=\frac{v_t}{1-{\beta }_2^t} \end{gathered}$$
   其中，${\hat{m}}_t$ 和${\hat{v}}_t$ 是校正后的一阶和二阶动量估计。

   推导：

   假设梯度 $g_t$是一个平稳的随机变量，其期望为：
   $$E(g_t)=\mu$$
   根据指数加权平均的递推公式，我们可以递推计算 $m_t$的期望。

   当t=1：
   $$m_1=\beta \cdot m_0+(1-\beta )\cdot g_1$$
   假设 $m_0=0$，所以：
   $$m_1=(1-\beta )\cdot g_1$$
   取期望：
   $$E(m1)=(1-\beta )\cdot E(g_1)=(1-\beta )\cdot \mu$$
   当t=2：
   $$m_2=\beta \cdot m_1+(1-\beta )\cdot g_2$$
   代入 $m_1=(1-\beta )\cdot g_1$：
   $$m_2=\beta \cdot (1-\beta )\cdot g_1+(1-\beta )\cdot g_2$$
   取期望：
   $$E(m_2)=\beta \cdot (1-\beta )\cdot E(g_1)+(1-\beta )\cdot E(g_2)=\beta (1-\beta )\cdot \mu +(1-\beta )\cdot \mu =(1-{\beta }^2)\cdot \mu$$
   当t=3：
   $$m_3=\beta \cdot m_2+(1-\beta )\cdot g_3$$
   代入 $m_2=\beta (1-\beta )\cdot g_1+(1-\beta )\cdot g_2$：
   $$m_3=\beta \cdot [\beta (1-\beta )\cdot g_1+(1-\beta )\cdot g_2]+(1-\beta )\cdot g_3$$
   展开：
   $$m_3={\beta }^2(1-\beta )\cdot g_1+\beta (1-\beta )\cdot g_2+(1-\beta )\cdot g_3$$
   取期望：
   $$E(m_3)={\beta }^2(1-\beta )\cdot \mu +\beta (1-\beta )\cdot \mu +(1-\beta )\cdot \mu =(1-{\beta }^3)\cdot \mu$$
   通过递推可以发现，对于任意时刻 t，$m_t$的期望为：
   $$E(m_t)=(1-{\beta }^t)\cdot \mu$$
   通过上述公式我们发现$m_t$的期望与梯度期望相差了$(1-{\beta }^t)$倍，我们想要找到一个修正后的$\widehat{m_t}$，使：$E(\widehat{m_t})=\mu$

   所以：
   $$E(m_t)=(1-{\beta }^t)\cdot \mu =(1-{\beta }^t)\cdot E(\widehat{m_t})$$
   进行缩放：
   $$m_t=(1-{\beta }^t)\cdot \widehat{m_t}$$
   得出：
   $$\widehat{m_t}=\frac{m_t}{1-{\beta }^t}$$
   $v_t$推导同理。

6. 参数更新：

   • 使用校正后的动量估计更新参数：
     $${\theta }_{t+1}={\theta }_t-\frac{\eta }{\sqrt{{\hat{v}}_t}+ϵ}{\hat{m}}_t$$

优点

1. 高效稳健：Adam结合了动量法和RMSProp的优势，在处理非静态、稀疏梯度和噪声数据时表现出色，能够快速稳定地收敛。

2. 自适应学习率：Adam通过一阶和二阶动量的估计，自适应调整每个参数的学习率，避免了全局学习率设定不合适的问题。

3. 适用大多数问题：Adam几乎可以在不调整超参数的情况下应用于各种深度学习模型，表现良好。

缺点

1. 超参数敏感：尽管Adam通常能很好地工作，但它对初始超参数（如 ${\beta }_1$、${\beta }_2$ 和 $\eta$）仍然较为敏感，有时需要仔细调参。

2. 过拟合风险：由于Adam会在初始阶段快速收敛，可能导致模型陷入局部最优甚至过拟合。因此，有时会结合其他优化算法（如SGD）使用。

2.5 总结

​ 梯度下降算法通过不断更新参数来最小化损失函数，是反向传播算法中计算权重调整的基础。在实际应用中，根据数据的规模和计算资源的情况，选择合适的梯度下降方式（批量、随机、小批量）及其变种（如动量法、Adam等）可以显著提高模型训练的效率和效果。

​ Adam是目前最为流行的优化算法之一，因其稳定性和高效性，广泛应用于各种深度学习模型的训练中。Adam结合了动量法和RMSProp的优点，能够在不同情况下自适应调整学习率，并提供快速且稳定的收敛表现。

示例：

    # 定义模型和损失函数
    model = nn.Linear(10, 1)
    criterion = nn.MSELoss()
    optimizer = torch.optim.Adam(model.parameters(), lr=0.01, betas=(0.9, 0.999), eps=1e-8)

    # 模拟数据
    X = torch.randn(100, 10)
    y = torch.randn(100, 1)

    # 训练循环
    for epoch in range(100):
        optimizer.zero_grad()
        outputs = model(X)
        loss = criterion(outputs, y)
        loss.backward()
        optimizer.step()
        print(f'Epoch {epoch}, Loss: {loss.item():.4f}')

七、过拟合与欠拟合

​ 在训练深层神经网络时，由于模型参数较多，在数据量不足时很容易过拟合。而正则化技术主要就是用于防止过拟合，提升模型的泛化能力(对新数据表现良好)和鲁棒性（对异常数据表现良好）。

1. 概念认知

这里我们简单的回顾下过拟合和欠拟合的基本概念~

1.1 过拟合

过拟合是指模型对训练数据拟合能力很强并表现很好，但在测试数据上表现较差。

过拟合常见原因有：

1. 数据量不足：当训练数据较少时，模型可能会过度学习数据中的噪声和细节。
2. 模型太复杂：如果模型很复杂，也会过度学习训练数据中的细节和噪声。
3. 正则化强度不足：如果正则化强度不足，可能会导致模型过度学习训练数据中的细节和噪声。

举个例子：

1.2 欠拟合

欠拟合是由于模型学习能力不足，无法充分捕捉数据中的复杂关系。

1.3 如何判断

那如何判断一个错误的结果是过拟合还是欠拟合呢？

过拟合

​ 训练误差低，但验证时误差高。模型在训练数据上表现很好，但在验证数据上表现不佳，说明模型可能过度拟合了训练数据中的噪声或特定模式。

欠拟合

​ 训练误差和测试误差都高。模型在训练数据和测试数据上的表现都不好，说明模型可能太简单，无法捕捉到数据中的复杂模式。

2. 解决欠拟合

欠拟合的解决思路比较直接：

1. 增加模型复杂度：引入更多的参数、增加神经网络的层数或节点数量，使模型能够捕捉到数据中的复杂模式。
2. 增加特征：通过特征工程添加更多有意义的特征，使模型能够更好地理解数据。
3. 减少正则化强度：适当减小 L1、L2 正则化强度，允许模型有更多自由度来拟合数据。
4. 训练更长时间：如果是因为训练不足导致的欠拟合，可以增加训练的轮数或时间.

3. 解决过拟合

避免模型参数过大是防止过拟合的关键步骤之一。

模型的复杂度主要由权重w决定，而不是偏置b。偏置只是对模型输出的平移，不会导致模型过度拟合数据。

怎么控制权重w，使w在比较小的范围内？

考虑损失函数，损失函数的目的是使预测值与真实值无限接近，如果在原来的损失函数上添加一个非0的变量
$$L_1(\hat{y},y)=L(\hat{y},y)+f(w)$$
其中$f(w)$是关于权重w的函数，$f(w)>0$

要使L1变小，就要使L变小的同时，也要使$f(w)$变小。从而控制权重w在较小的范围内。

3.1 L2正则化

L2 正则化通过在损失函数中添加权重参数的平方和来实现，目标是惩罚过大的参数值。

3.1.1 数学表示

设损失函数为 $L(\theta )$，其中 $\theta$ 表示权重参数，加入L2正则化后的损失函数表示为：
$$L_{\text{total}}(\theta )=L(\theta )+\lambda \cdot \frac{1}{2}\sum _i{\theta }_i^2$$
其中：

• $L(\theta )$ 是原始损失函数（比如均方误差、交叉熵等）。
• $\lambda$ 是正则化强度，控制正则化的力度。
• ${\theta }_i$ 是模型的第 $i$ 个权重参数。
• $\frac{1}{2}{\sum }_i{\theta }_i^2$ 是所有权重参数的平方和，称为 L2 正则化项。

L2 正则化会惩罚权重参数过大的情况，通过参数平方值对损失函数进行约束。

为什么是$\frac{\lambda }{2}$？

假设没有1/2，则对L2 正则化项${\theta }_i$的梯度为：$2\lambda {\theta }_i$，会引入一个额外的系数 2，使梯度计算和更新公式变得复杂。

添加1/2后，对${\theta }_i$的梯度为：$\lambda {\theta }_i$。

3.1.2 梯度更新

在 L2 正则化下，梯度更新时，不仅要考虑原始损失函数的梯度，还要考虑正则化项的影响。更新规则为：
$${\theta }_{t+1}={\theta }_t-\eta \left(\nabla L({\theta }_t)+\lambda {\theta }_t\right)$$
其中：

• $\eta$ 是学习率。
• $\nabla L({\theta }_t)$ 是损失函数关于参数${\theta }_t$ 的梯度。
• $\lambda {\theta }_t$ 是 L2 正则化项的梯度，对应的是参数值本身的衰减。

很明显，参数越大惩罚力度就越大，从而让参数逐渐趋向于较小值，避免出现过大的参数。

3.1.3 作用

1. 防止过拟合：当模型过于复杂、参数较多时，模型会倾向于记住训练数据中的噪声，导致过拟合。L2 正则化通过抑制参数的过大值，使得模型更加平滑，降低模型对训练数据噪声的敏感性。

2. 限制模型复杂度：L2 正则化项强制权重参数尽量接近 0，避免模型中某些参数过大，从而限制模型的复杂度。通过引入平方和项，L2 正则化鼓励模型的权重均匀分布，避免单个权重的值过大。

3. 提高模型的泛化能力：正则化项的存在使得模型在测试集上的表现更加稳健，避免在训练集上取得极高精度但在测试集上表现不佳。

4. 平滑权重分布：L2 正则化不会将权重直接变为 0，而是将权重值缩小。这样模型就更加平滑的拟合数据，同时保留足够的表达能力。

3.1.4 代码实现

代码实现如下：

import torch
import torch.nn as nn
import torch.optim as optim
import matplotlib.pyplot as plt

# 设置随机种子以保证可重复性
torch.manual_seed(42)

# 生成随机数据
n_samples = 100
n_features = 20
X = torch.randn(n_samples, n_features)  # 输入数据
y = torch.randn(n_samples, 1)  # 目标值


# 定义一个简单的全连接神经网络
class SimpleNet(nn.Module):
    def __init__(self):
        super(SimpleNet, self).__init__()
        self.fc1 = nn.Linear(n_features, 50)
        self.fc2 = nn.Linear(50, 1)

    def forward(self, x):
        x = torch.relu(self.fc1(x))
        return self.fc2(x)


# 训练函数
def train_model(use_l2=False, weight_decay=0.01, n_epochs=100):
    # 初始化模型
    model = SimpleNet()
    criterion = nn.MSELoss()  # 损失函数（均方误差）

    # 选择优化器
    if use_l2:
        optimizer = optim.SGD(model.parameters(), lr=0.01, weight_decay=weight_decay)  # 使用 L2 正则化
    else:
        optimizer = optim.SGD(model.parameters(), lr=0.01)  # 不使用 L2 正则化

    # 记录训练损失
    train_losses = []

    # 训练过程
    for epoch in range(n_epochs):
        optimizer.zero_grad()  # 清空梯度
        outputs = model(X)  # 前向传播
        loss = criterion(outputs, y)  # 计算损失
        loss.backward()  # 反向传播
        optimizer.step()  # 更新参数

        train_losses.append(loss.item())  # 记录损失

        if (epoch + 1) % 10 == 0:
            print(f'Epoch [{epoch + 1}/{n_epochs}], Loss: {loss.item():.4f}')

    return train_losses


# 训练并比较两种模型
train_losses_no_l2 = train_model(use_l2=False)  # 不使用 L2 正则化
train_losses_with_l2 = train_model(use_l2=True, weight_decay=0.01)  # 使用 L2 正则化

# 绘制训练损失曲线
plt.plot(train_losses_no_l2, label='Without L2 Regularization')
plt.plot(train_losses_with_l2, label='With L2 Regularization')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.title('Training Loss: L2 Regularization vs No Regularization')
plt.legend()
plt.show()

3.2 L1正则化

L1 正则化通过在损失函数中添加权重参数的绝对值之和来约束模型的复杂度。

3.2.1 数学表示

设模型的原始损失函数为 $L(\theta )$，其中 $\theta$ 表示模型权重参数，则加入 L1 正则化后的损失函数表示为：
$$L_{\text{total}}(\theta )=L(\theta )+\lambda \sum _i|{\theta }_i|$$
其中：

• $L(\theta )$ 是原始损失函数。
• $\lambda$ 是正则化强度，控制正则化的力度。
• $|{\theta }_i|$ 是模型第$i$ 个参数的绝对值。
• ${\sum }_i|{\theta }_i|$ 是所有权重参数的绝对值之和，这个项即为 L1 正则化项。

3.2.2 梯度更新

在 L1 正则化下，梯度更新时的公式是：
$${\theta }_{t+1}={\theta }_t-\eta \left(\nabla L({\theta }_t)+\lambda \cdot \text{sign}({\theta }_t)\right)$$
其中：

• $\eta$ 是学习率。
• $\nabla L({\theta }_t)$ 是损失函数关于参数 $\theta_t $ 的梯度。
• $\text{sign}({\theta }_t)$ 是参数 ${\theta }_t$ 的符号函数，表示当 ${\theta }_t$ 为正时取值为 $1$，为负时取值为 $-1$，等于 0 时为 $0$。

因为 L1 正则化依赖于参数的绝对值，其梯度更新时不是简单的线性缩小，而是通过符号函数来直接调整参数的方向。这就是为什么 L1 正则化能促使某些参数完全变为 0。

3.2.3 作用

1. 稀疏性：L1 正则化的一个显著特性是它会促使许多权重参数变为 零。这是因为 L1 正则化倾向于将权重绝对值缩小到零，使得模型只保留对结果最重要的特征，而将其他不相关的特征权重设为零，从而实现 特征选择 的功能。

2. 防止过拟合：通过限制权重的绝对值，L1 正则化减少了模型的复杂度，使其不容易过拟合训练数据。相比于 L2 正则化，L1 正则化更倾向于将某些权重完全移除，而不是减小它们的值。

3. 简化模型：由于 L1 正则化会将一些权重变为零，因此模型最终会变得更加简单，仅依赖于少数重要特征。这对于高维度数据特别有用，尤其是在特征数量远多于样本数量的情况下。

4. 特征选择：因为 L1 正则化会将部分权重置零，因此它天然具有特征选择的能力，有助于自动筛选出对模型预测最重要的特征。

3.2.4 与L2对比

• L1 正则化 更适合用于产生稀疏模型，会让部分权重完全为零，适合做特征选择。
• L2 正则化 更适合平滑模型的参数，避免过大参数，但不会使权重变为零，适合处理高维特征较为密集的场景。

3.2.5 代码实现

代码需要自己实现：

l1_lambda = 0.001
# 计算 L1 正则化项并将其加入到总损失中
l1_norm = sum(p.abs().sum() for p in model.parameters())
loss = loss + l1_lambda * l1_norm

3.3 Dropout

Dropout 的工作流程如下：

1. 在每次训练迭代中，随机选择一部分神经元（通常以概率 p丢弃，比如 p=0.5）。
2. 被选中的神经元在当前迭代中不参与前向传播和反向传播。
3. 在测试阶段，所有神经元都参与计算，但需要对权重进行缩放（通常乘以 1−p），以保持输出的期望值一致。

Dropout 是一种在训练过程中随机丢弃部分神经元的技术。它通过减少神经元之间的依赖来防止模型过于复杂，从而避免过拟合。

3.3.1 基本实现

import torch
import torch.nn as nn


def dropout():
    dropout = nn.Dropout(p=0.5)
    x = torch.randint(0, 10, (5, 6), dtype=torch.float)
    print(x)
    # 开始dropout
    print(dropout(x))


if __name__ == "__main__":
    dropout()

Dropout过程：

1. 按照指定的概率把部分神经元的值设置为0；
2. 为了规避该操作带来的影响，需对非 0 的元素使用缩放因子$$1/(1-p)$$进行强化。

假设某个神经元的输出为 x，Dropout 的操作可以表示为：

• 在训练阶段：
  $$y=\{\begin{array}{ll}\frac{x}{1-p}& 以概率1-p保留神经元\\ 0& 以概率p丢弃神经元\end{array}$$

• 在测试阶段：
  $$y=x$$

为什么要使用缩放因子$$1/(1-p)$$？

在训练阶段，Dropout 会以概率 p随机将某些神经元的输出设置为 0，而以概率 1−p 保留这些神经元。

假设某个神经元的原始输出是 x，那么在训练阶段，它的期望输出值为：
$$E(y_{train})=(1-p)\cdot (\frac{x}{1-p})+p\cdot 0=x$$
通过这种缩放，训练阶段的期望输出值仍然是 x，与没有 Dropout 时一致。

3.3.2 权重影响

import torch
import torch.nn as nn


def test001():
    torch.manual_seed(0)
    w = torch.randn(12, 1, requires_grad=True)
    x = torch.randint(0, 8, (3, 12)).float()
    output = x @ w
    output = output.sum()
    output.backward()
    print(w.grad.flatten())


def test002():
    torch.manual_seed(0)
    dropout = nn.Dropout(0.8)
    w = torch.randn(12, 1, requires_grad=True)
    x = torch.randint(0, 8, (3, 12)).float()
    # 随机抛点
    x = dropout(x)
    print(x)
    output = x @ w
    output = output.sum()
    output.backward()
    print(w.grad.flatten())


if __name__ == "__main__":
    test001()
    test002()

输出结果：如果所有的数据的对应特征都为0，则参数梯度为0

tensor([12., 15., 12.,  2.,  8.,  4.,  8.,  5., 13.,  7., 10., 15.])
tensor([[ 0.,  5., 25.,  0.,  0.,  0.,  0.,  0., 15.,  0., 15.,  0.],
        [ 0.,  0.,  0.,  0.,  0., 15.,  0.,  0.,  0.,  0.,  0.,  0.],
        [30.,  0.,  0.,  0.,  5.,  5.,  0.,  0.,  0.,  0.,  0.,  0.]])
tensor([30.,  5., 25.,  0.,  5., 20.,  0.,  0., 15.,  0., 15.,  0.])

示例：对图片进行随机丢弃

import torch
from torch import nn
from PIL import Image
from torchvision import transforms
import os

from matplotlib import pyplot as plt

torch.manual_seed(42)


def load_img(path, resize=(224, 224)):
    pil_img = Image.open(path).convert('RGB')
    print("Original image size:", pil_img.size)  # 打印原始尺寸
    transform = transforms.Compose([
        transforms.Resize(resize),
        transforms.ToTensor()  # 转换为Tensor并自动归一化到[0,1]
    ])
    return transform(pil_img)  # 返回[C,H,W]格式的tensor


if __name__ == '__main__':
    dirpath = os.path.dirname(__file__)
    path = os.path.join(dirpath, 'img', '100.jpg')  # 使用os.path.join更安全

    # 加载图像 (已经是[0,1]范围的Tensor)
    trans_img = load_img(path)

    # 添加batch维度 [1, C, H, W]，因为Dropout默认需要4D输入
    trans_img = trans_img.unsqueeze(0)

    # 创建Dropout层
    dropout = nn.Dropout2d(p=0.2)

    drop_img = dropout(trans_img)

    # 移除batch维度并转换为[H,W,C]格式供matplotlib显示
    trans_img = trans_img.squeeze(0).permute(1, 2, 0).numpy()
    drop_img = drop_img.squeeze(0).permute(1, 2, 0).numpy()

    # 确保数据在[0,1]范围内
    drop_img = drop_img.clip(0, 1)

    # 显示图像
    fig = plt.figure(figsize=(10, 5))

    ax1 = fig.add_subplot(1, 2, 1)
    ax1.imshow(trans_img)

    ax2 = fig.add_subplot(1, 2, 2)
    ax2.imshow(drop_img)

    plt.show()

效果：

说明：

nn.Dropout2d§:Dropout2d 是针对二维数据设计的 Dropout 层，它在训练过程中随机将输入张量的某些通道（二维平面）置为零。

参数	要求格式	示例形状	说明
输入	(N, C, H, W)	(16, 64, 32, 32)	批大小×通道×高×宽
输出	(N, C, H, W)	(16, 64, 32, 32)	与输入同形，部分通道归零

3.4 简化模型

• 减少网络层数和参数：
  通过减少网络的层数、每层的神经元数量或减少卷积层的滤波器数量，可以降低模型的复杂度，减少过拟合的风险。

• 使用更简单的模型：
  对于复杂问题，使用更简单的模型或较小的网络架构可以减少参数数量，从而降低过拟合的可能性。

3.5 数据增强

样本数量不足（即训练数据过少）是导致过拟合（Overfitting）的常见原因之一，可以从以下角度理解：

• 当训练数据过少时，模型容易“记住”有限的样本（包括噪声和无关细节），而非学习通用的规律。
• 简单模型更可能捕捉真实规律，但数据不足时，复杂模型会倾向于拟合训练集中的偶然性模式（噪声）。
• 样本不足时，训练集的分布可能与真实分布偏差较大，导致模型学到错误的规律。
• 小数据集中，个别样本的噪声（如标注错误、异常值）会被放大，模型可能将噪声误认为规律。

数据增强（Data Augmentation）是一种通过人工生成或修改训练数据来增加数据集多样性的技术，常用于解决过拟合问题。数据增强通过“模拟”更多训练数据，迫使模型学习泛化性更强的规律，而非训练集中的偶然性模式。其本质是一种低成本的正则化手段，尤其在数据稀缺时效果显著。

在了解计算机如何处理图像之前，需要先了解图像的构成元素。

图像是由像素点组成的，每个像素点的值范围为: [0, 255], 像素值越大意味着较亮。比如一张 200x200 的图像, 则是由 40000 个像素点组成, 如果每个像素点都是 0 的话, 意味着这是一张全黑的图像。

我们看到的彩色图一般都是多通道的图像, 所谓多通道可以理解为图像由多个不同的图像层叠加而成, 例如我们看到的彩色图像一般都是由 RGB 三个通道组成的，还有一些图像具有 RGBA 四个通道，最后一个通道为透明通道，该值越小，则图像越透明。

数据增强是提高模型泛化能力（鲁棒性）的一种有效方法，尤其在图像分类、目标检测等任务中。数据增强可以模拟更多的训练样本，从而减少过拟合风险。数据增强通过torchvision.transforms模块来实现。

数据增强的好处

​ 大幅度降低数据采集和标注成本；

​ 模型过拟合风险降低，提高模型泛化能力；

官方地址：

transforms：https://pytorch.org/vision/stable/transforms.html

transforms：

常用变换类

• transforms.Compose：将多个变换操作组合成一个流水线。
• transforms.ToTensor：将 PIL 图像或 NumPy 数组转换为 PyTorch 张量，将图像数据从 uint8 类型 (0-255) 转换为 float32 类型 (0.0-1.0)。
• transforms.Normalize：对张量进行标准化。
• transforms.Resize：调整图像大小。
• transforms.CenterCrop：从图像中心裁剪指定大小的区域。
• transforms.RandomCrop：随机裁剪图像。
• transforms.RandomHorizontalFlip：随机水平翻转图像。
• transforms.RandomVerticalFlip：随机垂直翻转图像。
• transforms.RandomRotation：随机旋转图像。
• transforms.ColorJitter：随机调整图像的亮度、对比度、饱和度和色调。
• transforms.RandomGrayscale：随机将图像转换为灰度图像。
• transforms.RandomResizedCrop：随机裁剪图像并调整大小。

3.5.1 图片缩放

具体参考官方文档：https://pytorch.org/vision/stable/auto_examples/transforms/plot_transforms_illustrations.html

参考代码：

from PIL import Image

def test03():
    img1 = plt.imread('./img/100.jpg')
    plt.imshow(img1)
    plt.show()

    img = Image.open('./img/100.jpg')
    transform = transforms.Compose([transforms.Resize((224, 224)), transforms.ToTensor()])
    r_img = transform(img)
    print(r_img.shape)

    r_img = r_img.permute(1, 2, 0)

    plt.imshow(r_img)
    plt.show()

3.5.2 随机裁剪

	img = Image.open('./img/100.jpg')
    transform = transforms.Compose([transforms.RandomCrop(size=(224, 224)), transforms.ToTensor()])
    r_img = transform(img)
    print(r_img.shape)

    r_img = r_img.permute(1, 2, 0)

    plt.imshow(r_img)
    plt.show()

3.5.3 随机水平翻转

RandomHorizontalFlip§：随机水平翻转图像，参数p表示翻转概率（0 ≤ p ≤ 1），p=1 表示必定翻转，p=0 表示不翻转

	img = Image.open('./img/100.jpg')
    transform = transforms.Compose([transforms.RandomHorizontalFlip(p=1), transforms.ToTensor()])
    r_img = transform(img)
    print(r_img.shape)

    r_img = r_img.permute(1, 2, 0)

    plt.imshow(r_img)
    plt.show()

3.5.4 调整图片颜色

transforms.ColorJitter(brightness=0, contrast=0, saturation=0, hue=0)

brightness：

• 亮度调整的范围。
• 可以float 或 (min, max) 元组：
  • 如果是 float（如 brightness=0.2），则亮度在 [max(0, 1 - 0.2), 1 + 0.2] = [0.8, 1.2] 范围内随机缩放。
  • 如果是 (min, max)（如 brightness=(0.5, 1.5)），则亮度在 [0.5, 1.5] 范围内随机缩放。

contrast：

• 对比度调整的范围。
• 格式与 brightness 相同。

saturation：

• 饱和度调整的范围。
• 格式与 brightness 相同。

hue：

• 色调调整的范围。
• 可以是一个浮点数（表示相对范围）或一个元组 (min, max)。
• 取值范围必须为 [-0.5, 0.5]（因为色相在 HSV 色彩空间中是循环的，超出范围会导致颜色异常）。
• 例如，hue=0.1 表示色调在 [-0.1, 0.1] 之间随机调整。

	img = Image.open('./img/100.jpg')
    transform = transforms.Compose([transforms.ColorJitter(brightness=0.2, contrast=0.2, saturation=0.2, hue=0.2), transforms.ToTensor()])
    r_img = transform(img)
    print(r_img.shape)

    r_img = r_img.permute(1, 2, 0)

    plt.imshow(r_img)
    plt.show()

3.5.5 随机旋转

RandomRotation用于对图像进行随机旋转。

transforms.RandomRotation(
    degrees, 
    interpolation=InterpolationMode.NEAREST, 
    expand=False, 
    center=None, 
    fill=0
)

degrees：

• 旋转角度的范围，可以是一个浮点数或元组 (min_degree, max_degree)。
• 例如，degrees=30 表示旋转角度在 [-30, 30] 之间随机选择。
• 例如，degrees=(30, 60) 表示旋转角度在 [30, 60] 之间随机选择。

interpolation：

• 插值方法，用于旋转图像。
• 默认是 InterpolationMode.NEAREST（最近邻插值）。
• 其他选项包括 InterpolationMode.BILINEAR（双线性插值）、InterpolationMode.BICUBIC（双三次插值）等。

expand：

• 是否扩展图像大小以适应旋转后的图像。如：当需要保留完整旋转后的图像时（如医学影像、文档扫描）
• 如果为 True，旋转后的图像可能会比原始图像大。
• 如果为 False，旋转后的图像大小与原始图像相同。

center：

• 旋转中心点的坐标，默认为图像中心。
• 可以是一个元组 (x, y)，表示旋转中心的坐标。

fill：

• 旋转后图像边缘的填充值。
• 可以是一个浮点数（用于灰度图像）或一个元组（用于 RGB 图像）。默认填充0(黑色)

	# 加载图像
    image = Image.open('./img/100.jpg')

    # 定义 RandomRotation 变换
    transform = transforms.RandomRotation(degrees=30)  # 旋转角度在 [-30, 30] 之间随机选择

    # 应用变换
    rotated_image = transform(image)

    # 显示图像
    plt.imshow(rotated_image)
    plt.axis('off')
    plt.show()

3.5.6 归一化

• 标准化：将图像的像素值从原始范围（如 [0, 255] 或 [0, 1]）转换为均值为 0、标准差为 1 的分布。
• 加速训练：标准化后的数据分布更均匀，有助于加速模型训练。
• 提高模型性能：标准化可以使模型更容易学习到数据的特征，提高模型的收敛性和稳定性。

    img = Image.open('./img/100.jpg')
    transform = transforms.Compose(
        [transforms.ToTensor(),
         transforms.Normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225])])
    r_img = transform(img)
    print(r_img.shape)

    r_img = r_img.permute(1, 2, 0)

    plt.imshow(r_img)
    plt.show()

mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225])]

均值（Mean）：数据集中所有图像在每个通道上的像素值的平均值。

标准差（Std）：数据集中所有图像在每个通道上的像素值的标准差。

RGB 三个通道的均值和标准差 不是随便定义的，而是需要根据具体的数据集进行统计计算。这些值是 ImageNet 数据集的统计结果，已成为计算机视觉任务的默认标准。

3.5.7 数据增强整合

使用transforms.Compose()把要增强的操作整合到一起：

from PIL import Image
from pathlib import Path
import matplotlib.pyplot as plt
import numpy as np
import torch
from torchvision import transforms, datasets, utils


def test01():
    # 定义数据增强和归一化
    transform = transforms.Compose(
        [
            transforms.RandomHorizontalFlip(),  # 随机水平翻转
            transforms.RandomRotation(10),  # 随机旋转 ±10 度
            transforms.RandomResizedCrop(
                32, scale=(0.8, 1.0)
            ),  # 随机裁剪到 32x32，缩放比例在0.8到1.0之间
            transforms.ColorJitter(
                brightness=0.2, contrast=0.2, saturation=0.2, hue=0.1
            ),  # 随机调整亮度、对比度、饱和度、色调
            transforms.ToTensor(),  # 转换为 Tensor
            transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5)),  # 归一化，这是一种常见的经验设置，适用于数据范围 [0, 1]，使其映射到 [-1, 1]
        ]
    )

    # 加载 CIFAR-10 数据集，并应用数据增强
    trainset = datasets.CIFAR10(root="./cifar10_data", train=True, download=True, transform=transform)
    dataloader = DataLoader(trainset, batch_size=4, shuffle=False)

    # 获取一个批次的数据
    images, labels = next(iter(dataloader))

    # 还原图片并显示
    plt.figure(figsize=(10, 5))
    for i in range(4):
        # 反归一化：将像素值从 [-1, 1] 还原到 [0, 1]
        img = images[i] / 2 + 0.5

        # 转换为 PIL 图像
        img_pil = transforms.ToPILImage()(img)

        # 显示图片
        plt.subplot(1, 4, i + 1)
        plt.imshow(img_pil)
        plt.axis('off')
        plt.title(f'Label: {labels[i]}')

    plt.show()


if __name__ == "__main__":
    test01()

代码解释：

transforms.Normalize(mean=[0.5, 0.5, 0.5], std=[0.5, 0.5, 0.5])

若数据分布与ImageNet差异较大（如医学影像、卫星图、MNIST等），或均值和标准差未知时，可用此简化设置。

将图片进行归一化，使数据更符合正态分布，归一化公式：
$$normalized\_img=\frac{img-0.5}{0.5}=2\times img-1$$

img = img / 2 + 0.5

表示反归一化，是归一化的逆运算：
$$img=\frac{normalized\_img+1}{2}=\frac{normalized\_img}{2}+0.5$$

数据集计算均值和标准差

以CIFAR10数据集为例：

# 获取数据集
train_data = datasets.CIFAR10(
    root='./cifar10',
    train=True,
    download=True,
    transform=transforms.ToTensor()  # 自动将PIL图像转为[0,1]范围的张量
)


def compute_mean_std(dataset):
    # 初始化累加器
    mean = torch.zeros(3)
    std = torch.zeros(3)
    num_samples = len(dataset)

    # 遍历数据集计算均值
    for img, _ in dataset:
        mean += img.mean(dim=(1, 2))  # 对每个通道的H,W维度求均值
    mean /= num_samples
    print(mean)

    # 遍历数据集计算标准差
    for img, _ in dataset:
        # 原始mean 是一个形状为 [3] 的张量，表示每个通道的均值。
        # 使用 view(3, 1, 1) 将 mean 的形状从 [3] 改变为 [3, 1, 1]。
        # 这样，mean 的形状变为 [3, 1, 1]，其中 3 表示通道数，1 和 1 分别表示高度和宽度的维度。
        # 当执行 img - mean.view(3, 1, 1) 时，PyTorch 会利用广播机制将 mean 自动扩展到与 img 相同的形状 [3, H, W]。
        # 然后利用方差公式计算：var=E(x-E(x))^2
        std += (img - mean.view(3, 1, 1)).pow(2).mean(dim=(1, 2))
    # 计算出所有图片的方差后，计算平均方差，然后求标准差
    std = torch.sqrt(std / num_samples)

    return mean, std


mean, std = compute_mean_std(train_data)
print(f"Mean: {mean}")  # 输出类似 [0.4914, 0.4822, 0.4465]
print(f"Std: {std}")  # 输出类似 [0.2470, 0.2435, 0.2616]

3.6 早停

​ 早停是一种在训练过程中监控模型在验证集上的表现，并在验证误差不再改善时停止训练的技术。这样可避免训练过度，防止模型过拟合。pytorch没有现成的API，需要自己写代码实现。

早停法的实现步骤

1. 将数据集分为训练集和验证集。
2. 在训练过程中，定期（例如每个 epoch）在验证集上评估模型的性能（如损失或准确率）。
3. 记录验证集的最佳性能（如最低损失或最高准确率）。
4. 如果验证集的性能在连续若干次评估中没有改善（即达到预设的“耐心值”），则停止训练。
5. 返回验证集性能最佳时的模型参数。

早停法的关键参数

1. 耐心值（Patience）：
   • 允许验证集性能不提升的连续次数。
   • 例如，如果耐心值为 5，则当验证集损失连续 5 次没有下降时，停止训练。
2. 最小改善值（Min Delta）：
   • 定义“性能提升”的最小阈值。
   • 例如，如果验证集损失的变化小于该值，则认为性能没有提升。
3. 恢复最佳权重（Restore Best Weights）：
   • 是否在早停时恢复验证集性能最佳时的模型权重。

示例(AI生成)：

import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import DataLoader, TensorDataset
from sklearn.model_selection import train_test_split
import numpy as np

# 1. 定义一个简单的神经网络
class SimpleNet(nn.Module):
    def __init__(self):
        super(SimpleNet, self).__init__()
        self.fc1 = nn.Linear(20, 64)
        self.fc2 = nn.Linear(64, 1)
        self.relu = nn.ReLU()

    def forward(self, x):
        x = self.relu(self.fc1(x))
        x = self.fc2(x)
        return x

# 2. 早停法类
class EarlyStopping:
    def __init__(self, patience=5, min_delta=0):
        """
        Args:
            patience (int): 允许验证集损失不提升的连续次数。
            min_delta (float): 定义“提升”的最小阈值。
        """
        self.patience = patience
        self.min_delta = min_delta
        self.counter = 0
        self.best_loss = None
        self.early_stop = False

    def __call__(self, val_loss):
        if self.best_loss is None:
            self.best_loss = val_loss
        elif val_loss > self.best_loss - self.min_delta:
            self.counter += 1
            if self.counter >= self.patience:
                self.early_stop = True
        else:
            self.best_loss = val_loss
            self.counter = 0

# 3. 生成一些随机数据
np.random.seed(42)
torch.manual_seed(42)

X = np.random.rand(1000, 20)  # 1000 个样本，每个样本 20 个特征
y = np.random.rand(1000, 1)   # 1000 个目标值

# 划分训练集和验证集
X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2, random_state=42)

# 转换为 PyTorch 张量
X_train = torch.tensor(X_train, dtype=torch.float32)
y_train = torch.tensor(y_train, dtype=torch.float32)
X_val = torch.tensor(X_val, dtype=torch.float32)
y_val = torch.tensor(y_val, dtype=torch.float32)

# 创建 DataLoader
train_dataset = TensorDataset(X_train, y_train)
train_loader = DataLoader(train_dataset, batch_size=32, shuffle=True)
val_dataset = TensorDataset(X_val, y_val)
val_loader = DataLoader(val_dataset, batch_size=32, shuffle=False)

# 4. 初始化模型、损失函数和优化器
model = SimpleNet()
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)

# 5. 初始化早停法
early_stopping = EarlyStopping(patience=5, min_delta=0.001)

# 6. 训练循环
num_epochs = 100
train_losses, val_losses = [], []

for epoch in range(num_epochs):
    model.train()
    epoch_train_loss = 0
    for X_batch, y_batch in train_loader:
        optimizer.zero_grad()
        outputs = model(X_batch)
        loss = criterion(outputs, y_batch)
        loss.backward()
        optimizer.step()
        epoch_train_loss += loss.item()
    train_losses.append(epoch_train_loss / len(train_loader))

    # 验证阶段
    model.eval()
    epoch_val_loss = 0
    with torch.no_grad():
        for X_batch, y_batch in val_loader:
            outputs = model(X_batch)
            loss = criterion(outputs, y_batch)
            epoch_val_loss += loss.item()
    val_losses.append(epoch_val_loss / len(val_loader))

    print(f"Epoch {epoch+1}/{num_epochs}, Train Loss: {train_losses[-1]:.4f}, Val Loss: {val_losses[-1]:.4f}")

    # 早停法检查
    early_stopping(val_losses[-1])
    if early_stopping.early_stop:
        print("Early stopping triggered!")
        break

# 7. 训练完成
print("Training complete!")

3.7 交叉验证

使用交叉验证技术可以帮助评估模型的泛化能力，并调整模型超参数，以防止模型在训练数据上过拟合。

这些方法可以单独使用，也可以结合使用，以有效地防止参数过大和过拟合。根据具体问题和数据集的特点，选择合适的策略来优化模型的性能。

八、批量标准化

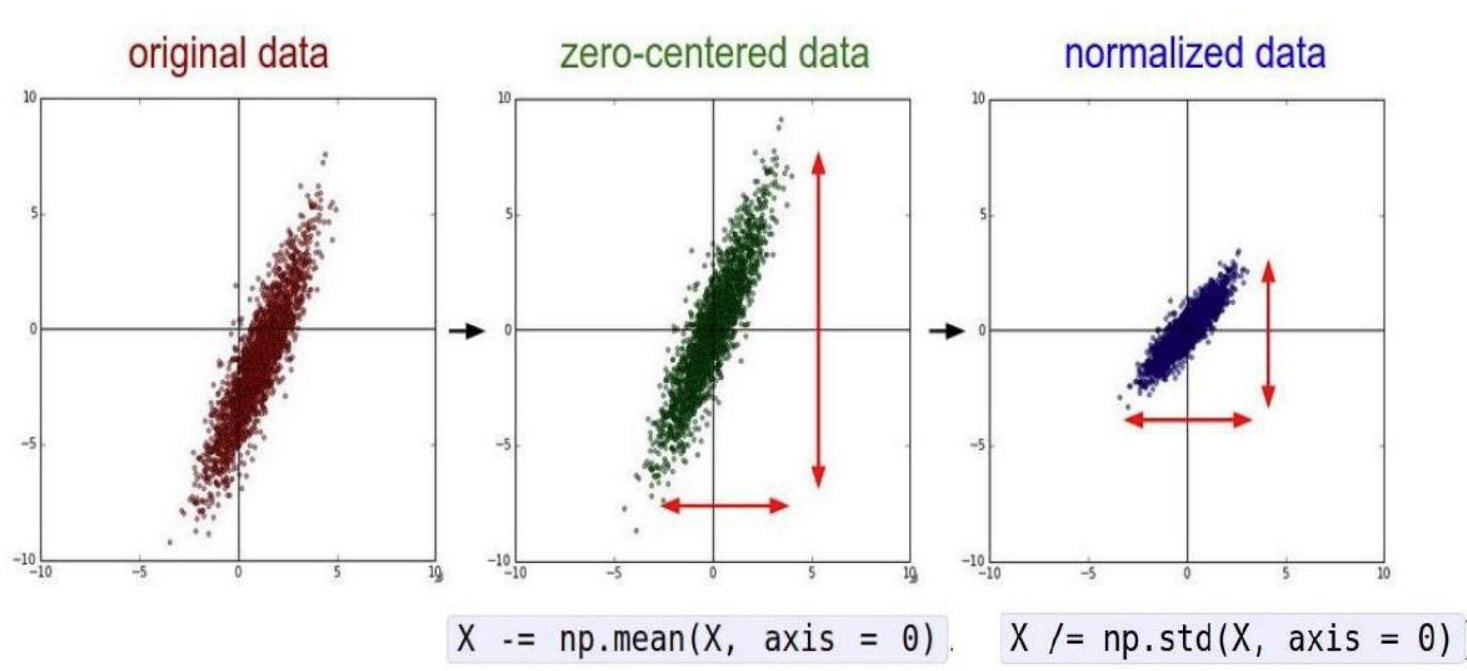
批量标准化（Batch Normalization, BN）是一种广泛使用的神经网络正则化技术，核心思想是对每一层的输入进行标准化，然后进行缩放和平移，旨在加速训练、提高模型的稳定性和泛化能力。批量标准化通常在全连接层或卷积层之后、激活函数之前应用。

核心思想

Batch Normalization（BN）通过对每一批（batch）数据的每个特征通道进行标准化，解决内部协变量偏移（Internal Covariate Shift）问题，从而：

• 加速网络训练
• 允许使用更大的学习率
• 减少对初始化的依赖
• 提供轻微的正则化效果

批量标准化的基本思路是在每一层的输入上执行标准化操作，并学习两个可训练的参数：缩放因子 $\gamma$ 和偏移量 $\beta$。

在深度学习中，批量标准化（Batch Normalization）在训练阶段和测试阶段的行为是不同的。在测试阶段，由于没有 mini-batch 数据，无法直接计算当前 batch 的均值和方差，因此需要使用训练阶段计算的全局统计量（均值和方差）来进行标准化。

官网地址：https://pytorch.org/docs/stable/nn.html#normalization-layers

1. 训练阶段的批量标准化

1.1 计算均值和方差

对于给定的神经网络层，假设输入数据为 x = { x 1 , x 2 , … , x m } \mathbf{x} = \{x_1, x_2, \ldots, x_m\} x={x1​,x2​,…,xm​}，其中 $m是$批次大小。我们首先计算该批次数据的均值和方差。

• 均值（Mean）
  $${\mu }_B=\frac{1}{m}\sum _{i=1}^m{x}_i$$

• 方差
  $${\sigma }_B^2=\frac{1}{m}\sum _{i=1}^m(x_i-{\mu }_B{)}^2$$

1.2 标准化

使用计算得到的均值和方差对数据进行标准化，使得每个特征的均值为0，方差为1。

• 标准化后的值
  $${\hat{x}}_i=\frac{x_i-{\mu }_B}{\sqrt{{\sigma }_B^2+ϵ}}$$
  其中，$ϵ$ 是一个很小的常数，防止除以零的情况。

1.3 缩放和平移

标准化后的数据通常会通过可训练的参数进行缩放和平移，以恢复模型的表达能力。

• 缩放（Gamma）：
  $$y_i=\gamma {\hat{x}}_i$$

• 平移（Beta）：
  $$y_i=\gamma {\hat{x}}_i+\beta$$
  其中，$\gamma$ 和 $\beta$ 是在训练过程中学习到的参数。它们会随着网络的训练过程通过反向传播进行更新。

1.4 更新全局统计量

通过指数移动平均（Exponential Moving Average, EMA）更新全局均值和方差：
$$\begin{gathered} {\mu }_{global}=(1-momentum)\cdot {\mu }_{global}+momentum\cdot {\mu }_B \\ {\sigma }_{global}^2=(1-momentum)\cdot {\sigma }_{global}^2+momentum\cdot {\sigma }_B^2 \end{gathered}$$
其中，momentum 是一个超参数，

控制当前 mini-batch 统计量对全局统计量的贡献。

momentum 是一个介于 0 和 1 之间的值，控制当前 mini-batch 统计量的权重。PyTorch 中 momentum 的默认值是 0.1。

与优化器中的 momentum 的区别

• 批量标准化中的 momentum：
  • 用于更新全局统计量（均值和方差）。
  • 控制当前 mini-batch 统计量对全局统计量的贡献。
• 优化器中的 momentum：
  • 用于加速梯度下降过程，帮助跳出局部最优。
  • 例如，SGD 优化器中的 momentum 参数。

两者虽然名字相同，但作用完全不同，不要混淆。

2. 测试阶段的批量标准化

在测试阶段，由于没有 mini-batch 数据，无法直接计算当前 batch 的均值和方差。因此，使用训练阶段通过 EMA 计算的全局统计量（均值和方差）来进行标准化。

在测试阶段，使用全局统计量对输入数据进行标准化：
$${\hat{x}}_i=\frac{x_i-{\mu }_{global}}{\sqrt{{\sigma }_{global}^2+ϵ}}$$
然后对标准化后的数据进行缩放和平移：
$$yi=\gamma \cdot {\hat{x}}_i+\beta$$
为什么使用全局统计量？

一致性：

• 在测试阶段，输入数据通常是单个样本或少量样本，无法准确计算均值和方差。
• 使用全局统计量可以确保测试阶段的行为与训练阶段一致。

稳定性：

• 全局统计量是通过训练阶段的大量 mini-batch 数据计算得到的，能够更好地反映数据的整体分布。
• 使用全局统计量可以减少测试阶段的随机性，使模型的输出更加稳定。

效率：

• 在测试阶段，使用预先计算的全局统计量可以避免重复计算，提高效率。

3. 作用

批量标准化（Batch Normalization, BN）通过以下几个方面来提高神经网络的训练稳定性、加速训练过程并减少过拟合：

3.1 缓解梯度问题

标准化处理可以防止激活值过大或过小，避免了激活函数（如 Sigmoid 或 Tanh）饱和的问题，从而缓解梯度消失或爆炸的问题。

3.2 加速训练

由于 BN 使得每层的输入数据分布更为稳定，因此模型可以使用更高的学习率进行训练。这可以加快收敛速度，并减少训练所需的时间。

3.3 减少过拟合

• 类似于正则化：虽然 BN 不是一种传统的正则化方法，但它通过对每个批次的数据进行标准化，可以起到一定的正则化作用。它通过在训练过程中引入了噪声（由于批量均值和方差的估计不完全准确），这有助于提高模型的泛化能力。

• 避免对单一数据点的过度拟合：BN 强制模型在每个批次上进行标准化处理，减少了模型对单个训练样本的依赖。这有助于模型更好地学习到数据的整体特征，而不是对特定样本的噪声进行过度拟合。

3.4函数说明

torch.nn.BatchNorm1d 是 PyTorch 中用于一维数据的批量标准化（Batch Normalization）模块。

torch.nn.BatchNorm1d(
    num_features,         # 输入数据的特征维度
    eps=1e-05,           # 用于数值稳定性的小常数
    momentum=0.1,        # 用于计算全局统计量的动量
    affine=True,         # 是否启用可学习的缩放和平移参数
    track_running_stats=True,  # 是否跟踪全局统计量
    device=None,         # 设备类型（如 CPU 或 GPU）
    dtype=None           # 数据类型
)

参数说明：

eps：用于数值稳定性的小常数，添加到方差的分母中，防止除零错误。默认值：1e-05

momentum：用于计算全局统计量（均值和方差）的动量。默认值：0.1，参考本节1.4

affine：是否启用可学习的缩放和平移参数（γ和 β）。如果 affine=True，则模块会学习两个参数；如果 affine=False，则不学习参数，直接输出标准化后的值 ${\hat{x}}_i$。默认值：True

track_running_stats：是否跟踪全局统计量（均值和方差）。如果 track_running_stats=True，则在训练过程中计算并更新全局统计量，并在测试阶段使用这些统计量。如果 track_running_stats=False，则不跟踪全局统计量，每次标准化都使用当前 mini-batch 的统计量。默认值：True

4. 代码实现

import torch
from torch import nn
from matplotlib import pyplot as plt

from sklearn.datasets import make_circles
from sklearn.model_selection import train_test_split
from torch.nn import functional as F
from torch import optim

# 数据准备
# 生成非线性可分数据（同心圆）
# n_samples	int	总样本数（默认100），内外圆各占一半
# noise	float	添加到数据中的高斯噪声标准差（默认0.0）
# factor	float	内圆与外圆的半径比（默认0.8）
# random_state	int	随机数种子，保证可重复性

# 输出数据
# X: 二维坐标数组，形状 (n_samples, 2)
# 每行是一个数据点的 [x, y] 坐标
# y: 类别标签 0（外圆）或 1（内圆），形状 (n_samples,)
x, y = make_circles(n_samples=2000, noise=0.1, factor=0.4, random_state=42)
x = torch.tensor(x, dtype=torch.float)
y = torch.tensor(y, dtype=torch.long)

x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random_state=42)

# 可视化原始训练数据和测试数据
plt.scatter(x[:, 0], x[:, 1], c=y, cmap='coolwarm', edgecolors='k')
plt.show()


# 定义BN模型
class NetWithBN(nn.Module):
    def __init__(self):
        super().__init__()
        self.fc1 = nn.Linear(2, 64)
        self.bn1 = nn.BatchNorm1d(64)
        self.fc2 = nn.Linear(64, 32)
        self.bn2 = nn.BatchNorm1d(32)
        self.fc3 = nn.Linear(32, 2)

    def forward(self, x):
        x = F.relu(self.bn1(self.fc1(x)))
        x = F.relu(self.bn2(self.fc2(x)))
        x = self.fc3(x)
        return x


# 定义无BN模型
class NetWithoutBN(nn.Module):
    def __init__(self):
        super().__init__()
        self.fc1 = nn.Linear(2, 64)
        self.fc2 = nn.Linear(64, 32)
        self.fc3 = nn.Linear(32, 2)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x


# 定义训练函数
def train(model, x_train, y_train, x_test, y_test, name, lr=0.1, epochs=500):
    criterion = nn.CrossEntropyLoss()
    optimizer = optim.SGD(model.parameters(), lr=lr)

    train_loss = []
    test_acc = []

    for epoch in range(epochs):
        model.train()
        y_pred = model(x_train)
        loss = criterion(y_pred, y_train)
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        train_loss.append(loss.item())

        model.eval()
        with torch.no_grad():
            y_test_pred = model(x_test)
            _, pred = torch.max(y_test_pred, dim=1)
            correct = (pred == y_test).sum().item()
            test_acc.append(correct / len(y_test))

        if epoch % 100 == 0:
            print(f'{name}|Epoch:{epoch},loss:{loss.item():.4f},acc:{test_acc[-1]:.4f}')
    return train_loss, test_acc


model_bn = NetWithBN()
model_nobn = NetWithoutBN()

bn_train_loss, bn_test_acc = train(model_bn, x_train, y_train, x_test, y_test, name='BN')
nobn_train_loss, nobn_test_acc = train(model_nobn, x_train, y_train, x_test, y_test, name='NoBN')


def plot(bn_train_loss, nobn_train_loss, bn_test_acc, nobn_test_acc):
    fig = plt.figure(figsize=(12, 5))
    ax1 = fig.add_subplot(1, 2, 1)
    ax1.plot(bn_train_loss, 'b', label='BN')
    ax1.plot(nobn_train_loss, 'r', label='NoBN')
    ax1.legend()

    ax2 = fig.add_subplot(1, 2, 2)
    ax2.plot(bn_test_acc, 'b', label='BN')
    ax2.plot(nobn_test_acc, 'r', label='NoBN')
    ax2.legend()
    plt.show()


plot(bn_train_loss, nobn_train_loss, bn_test_acc, nobn_test_acc)