陀螺仪目标角度与当前角度偏差计算

常见问题

当在角度PID控制中处理角度差时，陀螺仪测量的角度范围通常是0到180度以及0到-180度。在计算角度偏差时，常常会使用目标角度减去当前角度，即误差（error）等于目标角度减去当前角度（error = Target_angle - Now_angle）。然而，在角度从正向180度跨越到负向-179度时，继续使用该计算公式会导致误差突变，从而影响控制的稳定性

 

解决方法

方法一：分类讨论

这里我们采用分类讨论的方法去解决该问题。

 

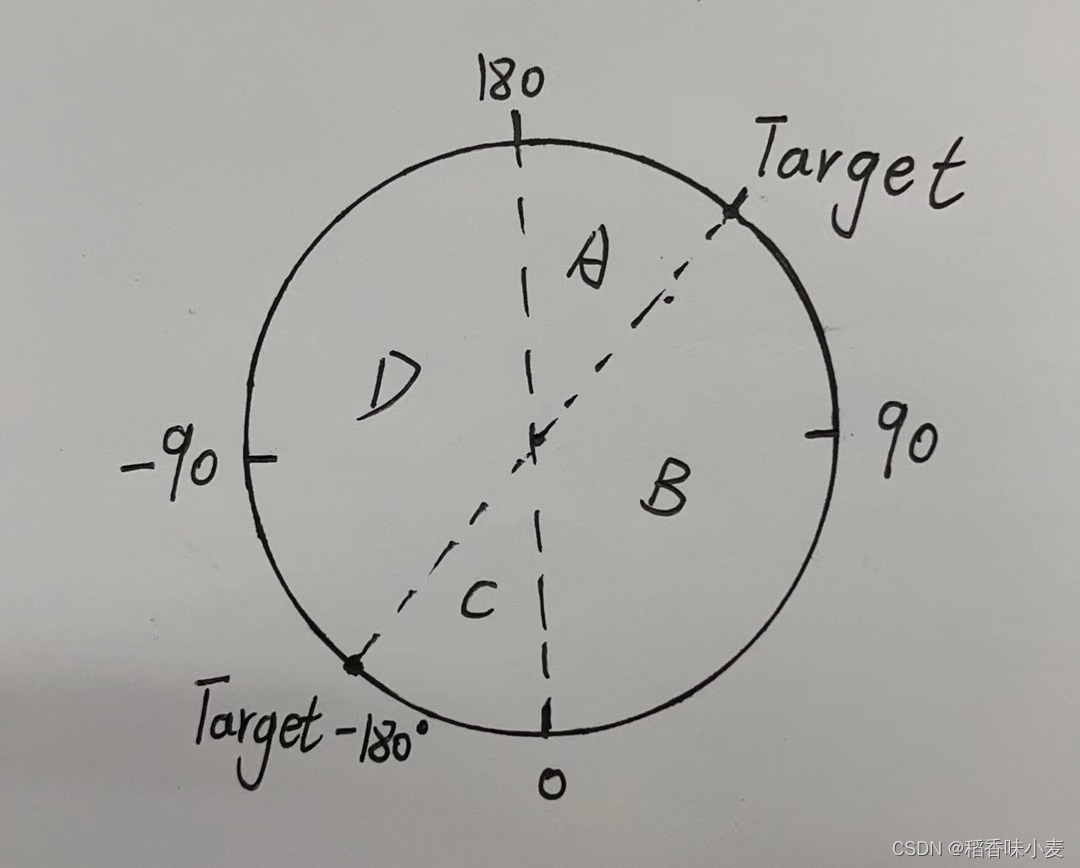
1. 目标角度为正（Target > 0）： 将角度范围划分为ABCD四个区域：

   • 当前角度位于AB区域，即Now_Angle > 0时，偏差error = Target - Now_Angle
   • 当前角度位于CD区域，即Now_Angle < 0时：
     • 若Now_Angle位于C区域，即Now_Angle > Target - 180，偏差error = |Now_Angle| + Target
     • 若Now_Angle位于D区域，即Now_Angle < Target - 180，偏差error = (Targht-180) - (180 + Now_Angle)

2. 目标角度为负（Target < 0）： 同样地，将角度范围划分为ABCD四个区域：

   • 当前角度位于AB区域，即Now_Angle < 0时，偏差error = Target - Now_Angle
   • 当前角度位于CD区域，即Now_Angle > 0时：
     • 若Now_Angle位于C区域，即Now_Angle > Target + 180，偏差error = Now_Angle - (180 + Target)
     • 若Now_Angle位于D区域，即Now_Angle < Target + 180，偏差error = Target - |Now_Angle|

在实际计算中，要确保明确正负方向，以正确应用分类讨论中的各种情况。这种方法应该能够帮助你处理陀螺仪角度在180度边界上的问题

注意计算时要标定好正方向

方法二：使用反正切函数

使用反正切函数（如atan2）来计算目标角度与当前角度的差值。这种方法会考虑角度的方向，因此不会在180度边界处产生不连续性。

方法三：角度归一化：

将角度映射到统一的范围，通常是-180度到+180度之间。当角度超过180度时，从角度中减去360度；当角度小于-180度时，从角度中加上360度，以确保角度保持在连续范围内。

代码实现

方法二和方法三代码就不贴出来了，个人觉得方法一简单方便，相比于方法二较简单，相对与方法三适合准确率更高。

float Yaw_error(float Target, float Now)
 {
    static float error;
    if (Target > 0) 
	{
        if (Now <= 0) 
		{
            if (fabs(Now) < (180 - Target)) 
			{
                error = fabs(Now) + Target;
            } 
			else 
			{
                error = -(180 - Target) - (180 - fabs(Now));
            }
        } 
		else 
		{
            if (Now > 0) 
			{
                error = Target - Now;
            }
        }
    } 
	else if (Target < 0)
	 {
        if (Now > 0) 
		{
            if (Now > Target + 180)
			{
                error = (180 - Now) + (180 - fabs(Target));
            }
			 else if (Now < Target + 180) 
			{
                error = -(fabs(Target) + Now);
            }
        } 
		else if (Now < 0) 
		{
            error = -(fabs(Target) - fabs(Now));
        }
    }
    
    return error;
}

float fabs(float value) {
    if (value < 0) 
	{
        return -value;
    } 
	else 
	{
        return value;
    }
}

 结语

上述问题常用于偏航角转过180度出现。如果如果上述有误，希望能点出，如果看不明白或者有问题可以加我QQ：2831194995一起讨论。