非线性规划（理论推导+python代码）

最新推荐文章于 2024-07-18 22:15:28 发布

会粗心的程序源

最新推荐文章于 2024-07-18 22:15:28 发布

阅读量1.6k

点赞数 16

文章标签：数学建模 python

本文链接：https://blog.csdn.net/m0_73951638/article/details/136104352

版权

前言

非线性规划相比线性规划更贴近现实，更一般化也更复杂一些。但是不要紧，我们先从最简单的无约束极值求法开始逐步深入到等号约束和不等号约束。

最开始我们不讲代码实现，因为python中封装好的函数针对的是最一般的情况，我们先从简单的情况开始，一步步到一般的情况，然后再到代码实现。

对理论不感兴趣，只想知道怎么用的朋友可以直接跳第五个标题目录。

一、高中一元函数的最值求法：

我们回忆一下高中倒数学过的内容：

如果我们要求一个函数的最值，是不是先把这个函数求导，找极值点，然后结合单调性把极值点和边界点都带进去验证？

看个高考题大家就明白了：

当然，这是最简单的情况，首先，它是一维的；其次，它的约束虽然是不等式约束，但只针对x，但我们只需要把区间的端点带入就可以避免约束带来的影响。

在实际情况中，我们碰到的往往是多变量的情况。

二、多变量无约束的最值求法：

这种情况下，我们只需要找出极值点，然后讨论变量的正负无穷的情况（如果变量有范围也可以这样讨论，只需要讨论边界情况即可）。

对于函数 $f(x_1,x_2,\cdots,x_n)$ ,若要求其最值，则需要通过下面的方程解出 $x_1,x_2,\cdots,x_n$

$\left\{\begin{matrix} \frac{\partial f}{\partial x_1}=0\\\\ \frac{\partial f}{\partial x_2}=0\\\\ \frac{\partial f}{\partial x_3}=0\\\cdots\cdots\end{matrix}\right.$

然后根据单调性带入就可以求得最值。

三、多变量等号约束的最值求法（拉格朗日数乘法）：

保险起见，这里先说一下约束是什么：

约束就是限制变量范围的式子，比如：

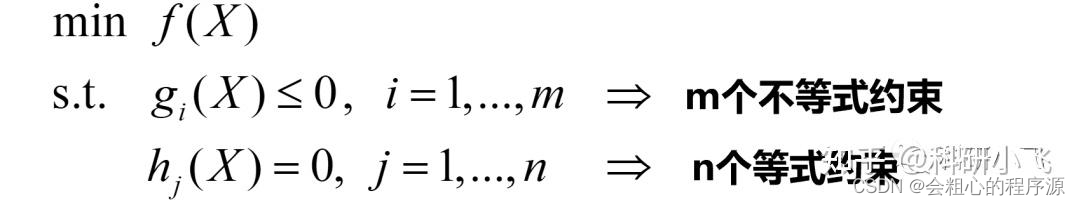
一般来说，这样的情况会用隐函数对目标函数的可行域进行约束。举个二元函数的例子：

$max\;z=f(x,y)\;s.t.\;\phi (x,y)=0$

通过下面的图片可以看到，本来是面的执行域被降维到了一维的曲线（虽然图不一定长这样哈）。

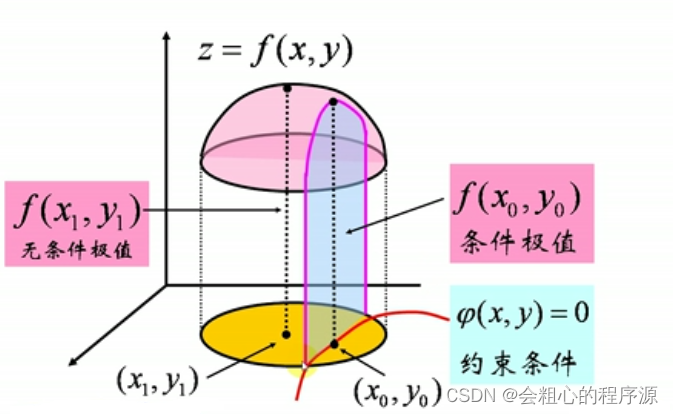
那么怎么在数值上把它计算出来呢？

执行域变了，方法也要变。这就需要请出我们高数下册（或者数分下册）的拉格朗日数乘法了。

我们构造拉格朗日函数： $L(x,y,\lambda )=f(x,y)+\lambda \phi(x,y)$

至于为什么这么构造，我一个不太严谨但比较直观的理解是： $\lambda\phi (x,y)=0$ ,所以加上后不影响结果，L(x,y,λ）的最值就是f(x,y)的最值，同时加上 $\lambda\phi (x,y)=0$ 后就将约束条件考虑了进去。对严谨的推导感兴趣的兄弟可以去看看课本咋写的。

然后通过下式求出x,y和λ：

$\left\{\begin{matrix} L_x(x,y,\lambda)=0\\ L_y(x,y,\lambda)=0\\ \phi (x,y)=0 \end{matrix}\right.$

然后就是带入求解了。

四、多变量等号约束+不等号约束的最值求法（KKT）：

好的，我们已经知道这个最值问题的求法了。

$max\;z=f(x,y)\;s.t.\;\phi (x,y)=0$

那么，如果稍微改一些：

$max\;z=f(x,y)\;s.t.\;\phi (x,y)\geqslant 0$

这又该怎么处理呢？

如果讨论更一般的情况：

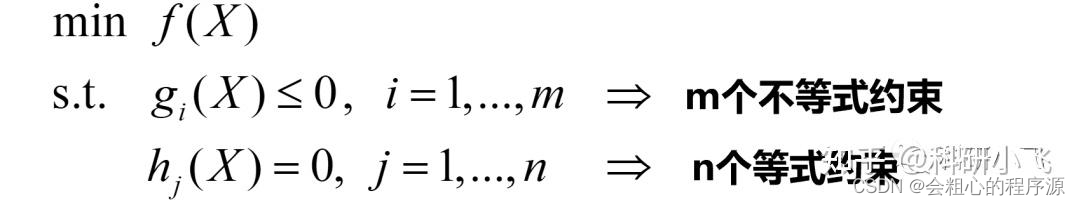
注：下面我会用我看了这篇文章后的理解阐释一遍kkt的大致思路，但我写的很粗略，所以还是建议大家看下这篇文章，里面有很多细节：KKT条件，原来如此简单 | 理论+算例实践 - 知乎 (zhihu.com)

这时候如果我们强行使用朗格朗日数乘法仅仅通过等式约束来解出极值点，很有可能解出来的极值点不在不等式约束的范围内，然后就要把解出来的结果都带入不等式约束中一一验证，得出的结果（X*）主要分为三种情况（我们可以事先预料到的情况）：

（1）g(X*)<0

此时该极值点在可行域内，符合条件，该解就是我们要找的可能的最优解。

（2）g(X*)=0

此时我们大可以用拉格朗日数乘法解决。

（3）g(X*)>0

不符合条件，舍弃。

顺着这个思路，kkt的发明人多想了一步：有没有可能把这个讨论也像构造拉格朗日函数那样融入到式子里？

然后就构造了下面这个式子：

一样的，求导：

这里很多兄弟懵了：（2）（4）式是什么玩意儿？

总结来说，（2）和（4）是分类讨论后总结出的必然情况。（2）的意思是λ和g(x)必然有一个是0：

（1）X*在可行域内（g(X*)<0），则我们仅仅使用等式约束求解出的结果是不是就可以用了？那我就没有任何必要去在构造式子的时候加上不等式约束了（λg(X*)），所以λ=0，λg(X*)=0。

（2）X*在可行域边界上（g(X*)=0），朗格朗日数乘法安排。一样的，λg(X*)=0。

（3）X*在可行域外（g(X*)>0），这咋办呢？不符合（5）舍掉哩。

综上λg(X*)=0。

五、python函数minimize的使用

说了那么多，但是以上都是理论知识，在解决问题的层面，我们要掌握的其实只有下面的函数：

参数很多，我们一个个来说

参数名称	参数内容
fun	我们需要求解的目标函数
x0	我们猜测的第一个最优解，猜测之后，计算机会从这个最优解出发开始迭代计算。
args	这个一般配合fun来组成目标函数，如图：但如果系数不复杂的话，建议直接在fun中定义好，这个系数个人认为没多大用
method	选择迭代计算的方式，有以下方式：
jac	雅可比矩阵或者梯度函数，相当于一阶导数（简化计算机的计算，节省时间）
hess	海森矩阵，相当于二阶导数（简化计算，节省时间），但很多method都用不到hess
hessp	海森矩阵乘一个向量，某些method中会用到
bounds	变量范围（比如0<x1<9）
constraints	多变量约束（隐函数约束,比如x1+x2<9）
tol	精度设置
callback	每次迭代后要调用的函数有以下形式 ``callback(xk, OptimizeResult state) -> bool`` 返回为TRUE则迭代终止 ``callback(xk)``
options	选项字典（可以自己选择是否要加上），如图，可以自行决定是否要限制最大迭代次数和是否需要展示结果

不过，如果看得懂英文文档，建议去官方文档细细读一下，比听我在这里胡诌强一万倍。

官方文档连接：

scipy.optimize.minimize — SciPy v1.12.0 Manual

六、实际的例子：

import numpy as np
from scipy import optimize as op
#fun : callable
#注意x的下标要从0开始依次往后递增，不然会报错
func=lambda x:(x[0]-1)**2+(x[1]-2.5)**2
""" bounds : sequence or `Bounds`, optional
        1. Instance of `Bounds` class——Bounds类
        2. Sequence of ``(min, max)`` pairs for each element in `x`. None
           is used to specify no bound——序列（或者说是由np.array构成的区间）"""
bound=np.array([[0,None],[0,None]])
#猜测解
x0=np.array([0,0])
#要使用字典的形式来增加约束
#注意x的下标也要从0开始依次往后递增，不然会报错
cons=({'type':'ineq','fun':lambda x:x[0]-2*x[1]+2},
      {'type':'ineq','fun':lambda x:-x[0]+2*x[1]+6},
      {'type':'ineq','fun':lambda x:-x[0]+2*x[1]+2})
res=op.minimize(func, x0,  bounds=bound, constraints=cons)
print(res)
print()
#注意这里增加了一个雅可比矩阵
res1=op.minimize(func,x0,  bounds=bound, jac=lambda x:np.array([2*(x[0]-1),2*(x[1]-2.5)]),constraints=cons)
print(res1)

贴个结果：

参数	含义
message	最优化程序是否正常终止
success	是否找到最优解
status	一个状态值，和终止的状态以及使用的方法有关
fun	目标方程的最小值
x	最小值点
nit	迭代次数
jac	雅可比矩阵（近似的）
nfev	程序检查方程的次数
njev	程序检查雅可比矩阵的次数

我们可以看到，加了雅可比矩阵后，程序检查方程的次数变少了，简化了计算。

最后，minimize只能求最小值，所以遇到这样的题目时，我们要转化一下：

$max\;z=f(x,y)\;s.t.\;\phi (x,y)\geqslant 0$

目标函数和约束条件都加个负号转化为：

$min\;-z=f(x,y)\;s.t.\;-\phi (x,y)\leqslant 0$

然后就可以套上面的流程来做了。

新手写文，有问题\错误请大家在评论区提出，如果觉得文章有用，不妨点个赞噢~

会粗心的程序源

关注

16
点赞
踩
21

收藏

觉得还不错? 一键收藏
0
评论
非线性规划（理论推导+python代码）

非线性规划相比线性规划更贴近现实，更一般化也更复杂一些。但是不要紧，我们先从最简单的无约束极值求法开始逐步深入到等号约束和不等号约束。最开始我们不讲代码实现，因为python中封装好的函数针对的是最一般的情况，我们先从简单的情况开始，一步步到一般的情况，然后再到代码实现。对理论不感兴趣，只想知道怎么用的朋友可以直接跳第五个标题目录。
复制链接

扫一扫