数学建模笔记（三）非线性规划和多目标优化

最新推荐文章于 2025-04-14 18:07:16 发布

lzrrrrr

最新推荐文章于 2025-04-14 18:07:16 发布

阅读量1.2w

点赞数 2

分类专栏：数学建模训练笔记文章标签：算法 python 数学建模

本文链接：https://blog.csdn.net/lzr_ps/article/details/107181013

版权

本文详细介绍了非线性规划的概念、数学模型和求解方法，包括凸规划的基本概念，通过实例展示了如何使用Lagrange乘数法和罚函数法解决有约束的非线性规划问题。此外，还探讨了多目标规划问题，如线性加权法、理想点法和优先级法等，并提供了实际应用的例子。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

文章目录

数学建模笔记（三）非线性规划和多目标优化

数学建模笔记（三）非线性规划和多目标优化

非线性规划概念和理论

非线性规划问题的数学模型

在这里插入图片描述

有约束非线性规划的求解

常见的处理思路是：可能的话将非线性问题转化为线性问题，将约束问题转化为无约束问题。
1.对有等式约束的非线性规划问题使用Lagrange乘数法求解
2.罚函数法：
利用目标函数和约束函数构造带参数的增广目标函数，从而转换成一系列无约束非线性规划问题来进行求解。

凸规划

基本概念：
1.凸集与凸函数的定义
凸集：
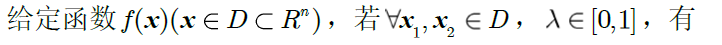
在这里插入图片描述凸函数：
例题1.
求解：
先对目标函数和约束函数中的非线性函数求二阶行列式，若均大于0，则是凸优化问题。
求解代码：

import numpy as np
import cvxpy as cp
x=cp.Variable(2,pos=True)
obj=cp.Minimize(sum(x**2)-4*x[0]+4)
con=[-x[0]+x[1]-2<=0,
x[0]**2-x[1]+1<=0]
prob = cp.Problem(obj, con)
prob.solve(solver='CVXOPT')
print("最优值为:",round(prob.value,4))
print("最优解为：\n", np.round(x.value,4))
#-------------结果--------------
最优值为: 3.7989
最优解为：
 [0.5536 1.3064]