LeetCode-栈-柱状图中最大的矩形

最新推荐文章于 2025-05-29 18:01:04 发布

Wneosy

最新推荐文章于 2025-05-29 18:01:04 发布

阅读量639

点赞数 17

分类专栏： LeetCodeRecording 文章标签： leetcode 算法栈

本文链接：https://blog.csdn.net/m0_74014989/article/details/148259755

版权

LeetCodeRecording 专栏收录该内容

20 篇文章

订阅专栏

LeetCode-栈-柱状图中最大的矩形

✏️ 关于专栏：专栏用于记录 prepare for the coding test。

文章目录

LeetCode-栈-柱状图中最大的矩形

📝柱状图中最大的矩形

🎯题目描述

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

🔗题目链接：柱状图中最大的矩形

🔍 输入输出示例

示例 1:

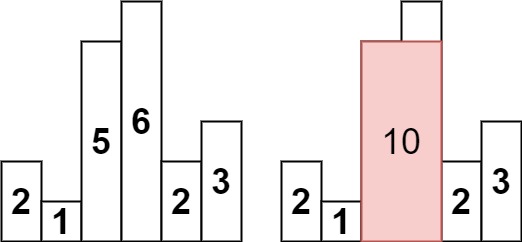
输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

示例 2:

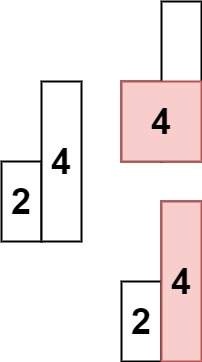
输入： heights = [2,4]
输出： 4

🧩题目提示

1 <= heights.length <=105
0 <= heights[i] <= 104

🧪AC

柱状图最大矩形问题的关键，在于每根柱子最多能向左右扩展多远，从而构成以它为高度的最大矩形。我们要解决的问题是：

对于每个 heights[i]，它作为矩形的最矮边时，最大能扩展多宽？

这可以转化为一个典型的“区间扩展”问题，我们需要找到：

左边第一个小于当前柱子的柱子（即扩展左边界）
右边第一个小于当前柱子的柱子（即扩展右边界）

为什么是“第一个小于”？

如果左边（或右边）是大于等于当前柱子高度的，它仍然可以作为矩形的一部分；
但一旦遇到更矮的柱子，就必须停止扩展，因为矩形的最低边界会被改变。

我们希望快速、准确地找到每个柱子左右第一个比它小的柱子。显然，暴力法时间复杂度为 $O(n^2)$ ，在数据量较大时无法通过。

这正是单调栈的优势场景：

栈中元素按柱子高度“递增”排列；
每当遇到一个新的柱子 heights[i]：
- 如果它比栈顶元素矮，说明栈顶元素的“右边第一个小于它”的柱子已经出现了。
- 此时出栈并更新其右边界。
同理，在元素入栈时，可以顺便更新其左边界。

通过这个过程，我们可以在 一趟遍历内同时完成左右边界的查找，并用公式计算每个柱子作为最低边的最大面积。

定义左右边界数组：

left[i]：左侧第一个比 heights[i] 小的柱子下标；
right[i]：右侧第一个比 heights[i] 小的柱子下标。

单调栈维护：

遍历一次计算 left[i]；
反向遍历计算 right[i]；
单调递增栈（栈顶到栈底高度逐渐减小）。

计算每根柱子的最大面积：

area = heights[i] * (right[i] - left[i] - 1)

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int n = heights.size();
        vector<int> left(n,-1);
        stack<int> st;
        for(int i = 0;i < n;i++){
            while(!st.empty() && heights[i] <= heights[st.top()]){
                st.pop();
            }
            if(!st.empty()){
                left[i] = st.top();
            }
            st.push(i);
        }
        vector<int> right(n,n);
        st = stack<int>();
        for(int i = n - 1;i >= 0;i--){
            while(!st.empty() && heights[i] <= heights[st.top()]){
                st.pop();
            }
            if(!st.empty()){
                right[i] = st.top();
            }
            st.push(i);
        }
        int ans = 0;
        for(int i = 0;i < n;i++){
            ans = max(ans,heights[i] * (right[i] - left[i] - 1));
        }
        return ans;
    }
};

相比解法一，此方法在一次遍历中同时维护 left 和更新 right：

如果当前柱子比栈顶矮，说明栈顶柱子的右边界就是当前下标；
当前栈顶就是当前柱子的左边界。

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int n = heights.size();
        vector<int> left(n,-1);
        vector<int> right(n,n);
        stack<int> st;
        for(int i = 0;i < n;i++){
            while(!st.empty() && heights[i] <= heights[st.top()]){
                right[st.top()] = i;
                st.pop();
            }
            if(!st.empty()){
                left[i] = st.top();
            }
            st.push(i);
        }
        int ans = 0;
        for(int i = 0;i < n;i++){
            ans = max(ans,heights[i] * (right[i] - left[i] - 1));
        }
        return ans;
    }
};

在末尾添加一个高度为 -1 的哨兵柱子，确保所有柱子都能及时被处理；

使用单调递增栈维护柱子的下标；

每次遇到当前柱子比栈顶矮，说明以栈顶柱子为最矮边的矩形结束了；

计算面积并更新最大值。

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        heights.push_back(-1);
        stack<int> st;
        st.push(-1);
        int ans = 0;
        int n = heights.size();
        for(int right = 0;right < n ;right++){
            while(st.size() > 1 && heights[right] <= heights[st.top()]){
                int i = st.top();
                st.pop();
                int left = st.top();
                ans = max(ans,heights[i] * (right - left - 1));
            }
            st.push(right);
        }
        return ans;
    }
};