1.体操队形
我们注意到该题的测试用例的范围非常的小，这种情况解法大概率就是暴力搜索/递归了。
解法：dfs
假如n = 4
对于每个位置，我们依次进行枚举，用pos记录当前枚举的位置。
递归出口，如果pos已经超过了n，说明这是一个合法位置，我们就让ret++，然后return。
接下来就是优化---剪枝部分了。
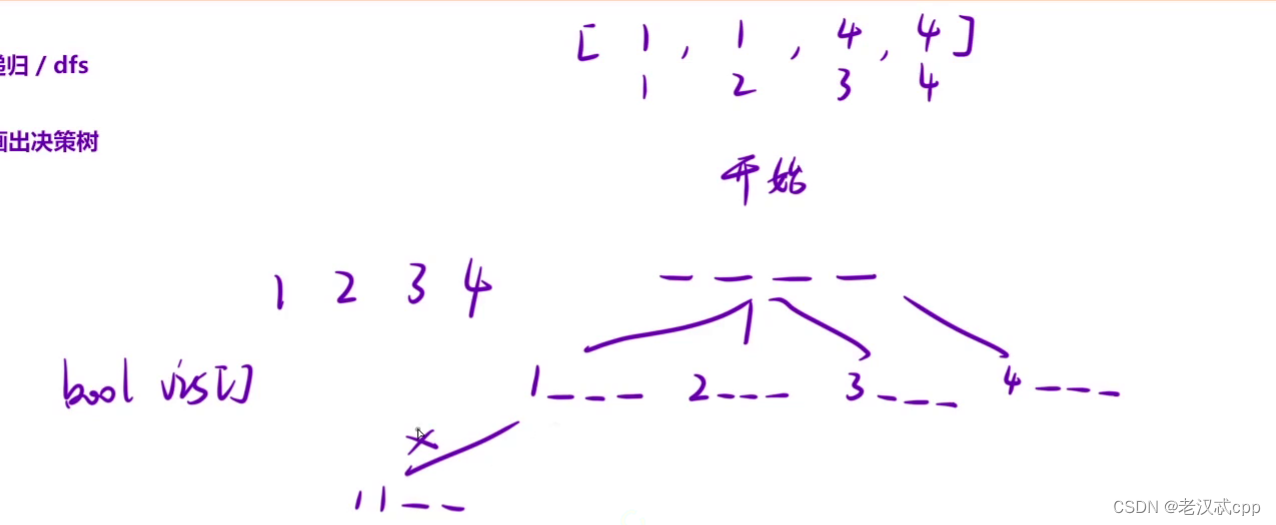
在我们的决策树当中，看看给出的示例，2号队员的诉求是要在1号的前面，那么如果我们先枚举了1号，在pos = 2时，1位置已经枚举1号了，也就是不能再出现了1号了，这里就是一个剪枝。
还有一个地方，依旧是这个场景下，当我们在pos == 2，枚举到2号时，发现不满足2号的诉求，那么我们可以想一下，如果1号依旧放在pos == 1的位置，那么后续无论2号放在哪里，这都是一个不合法的方案，那么我们直接剪掉1号在pos = 1位置的所有后续就可以了。
剪枝都做完了，递归将决策转化为代码的能力还是比较难的，代码：
另外要注意题，我们的数组下标最好从1开始。
#include <iostream>
using namespace std;
int arr[11] = {0};
bool vis[11] = {0};
int ret = 0;
int n;
void dfs(int pos)
{
if(pos == n + 1)
{
ret++;
return;
}
for(int i = 1; i <= n; ++i)
{
if(vis[i]) continue; // 说明这个位置已经用过了，剪枝
if(vis[arr[i]]) return; // 位置已经不合法了，剪枝
vis[i] = true;
dfs(pos + 1);
vis[i] = false; // 回溯
}
}
int main()
{
cin >> n;
for(int i = 1; i <= n; ++i)
cin >> arr[i];
dfs(1);
cout << ret << endl;
return 0;
}2.二叉树中的最大路径和
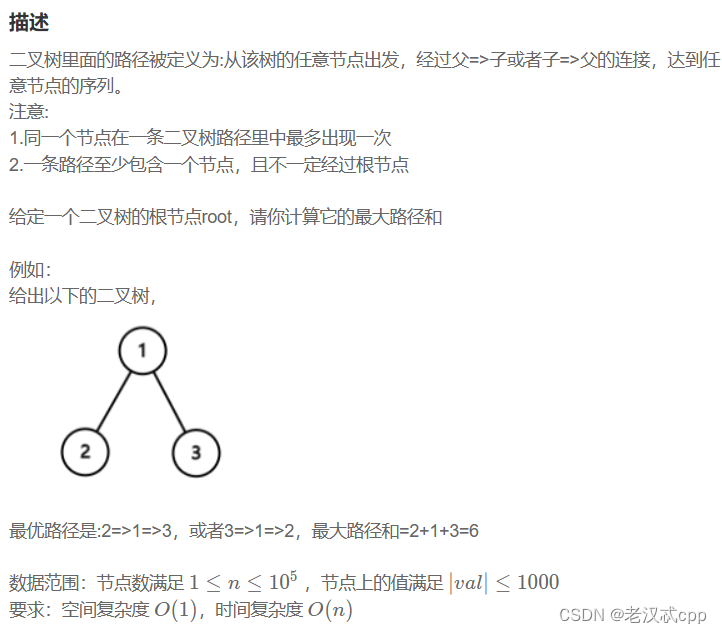
解法：dfs/树形dp。
树形dp比较少见，就是这个结点需要用到左子树和右子树的信息。
那么我们需要知道，在某棵子树上整理什么信息呢？（状态表示）：
经过根结点的最大路径和。
状态转移方程：
左子树提供：
以左子树为根的最大单链和。l = max(0,dfs(root->left)。
右子树提供：
以右子树的最大单链和。r = max(0,dfs(root->right)。
为什么要和0作比较取max呢？这是因为我们本来求的就是最大路径和，如果左子树（或右子树）提供的值还小于0，就不要它的值了。
然后我们可以定义一个全局的ret，ret = max(ret,l + r + root->val)。
那么我们每次递归该返回什么呢？（返回值）
我们不能返回 l + r + root->val，因为这不是以root为根结点形成的一条单链和。
虽然我们递归到某棵子树的时候，整理信息并更新ret是要用到 l + r + root->val，但是如果我们每次返回的是这个值的话，那么就会出现重复计算了，
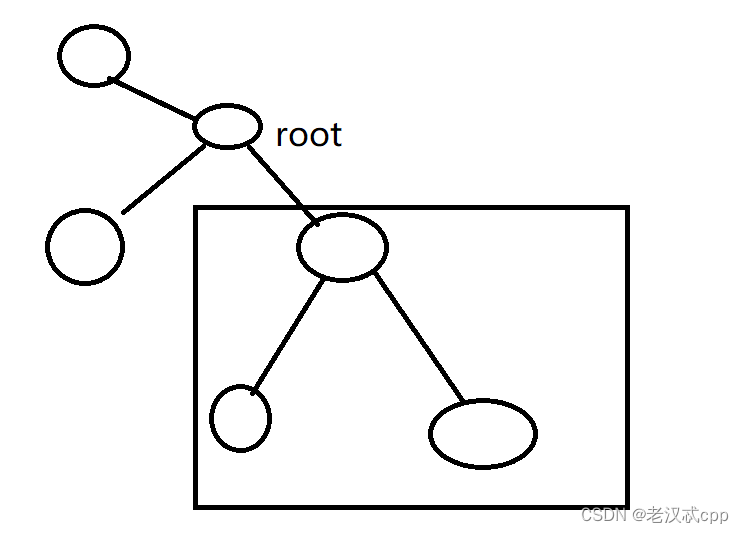
如图，当我们在分析root的时候，如果从右子树上提取的信息是右子树的l + r 右子树的root->val，的话，我们使用这个值分析root的时候，这条路径是不符合题意中的路径的。
所以我们的返回值是：
root->val + max(l,r)。
代码：
#include <climits>
class Solution {
public:
int ret = INT_MIN;
int dfs(TreeNode* root)
{
if(root == nullptr) return 0;
int left =max(0,dfs(root->left));
int right = max(0,dfs(root->right));
ret = max(ret,left + right + root->val);
return root->val + max(left,right);
}
int maxPathSum(TreeNode* root) {
ret = INT_MIN;
dfs(root);
return ret;
}
};
3.最长上升子序列（二）
这道题有两种解法：
1.动态规划。但是时间复杂度是O(N^2)，观察一下测试用例的数据范围，大概率是会超时的。
2.贪心 + 二分，时间复杂度O(n * logn)。
因此，本题使用贪心 + 二分的方式解决。
算法流程：
1.我们并不关心前面的子序列长什么样子，我们仅需要知道长度为 x 的子序列的末尾是多少即可。
2.存长度为x的子序列末尾时，我们仅需要存最小的值就可以了。（贪心）。
前面的两点是解决该题的核心思路，用到了贪心，但是此时时间复杂度是O(N^2)的，因此我们还需要进行优化。
假设我们用一个dp数组来存长度为x的子序列，我们可以用下标来映射该子序列的长度，比如0下标就代表这是一个长度为1的子序列。
以本题的测试用例 [1,4,7,5,6]，那么dp里面的元素依次是 1 4 5 6，我们发现是单调递增的，也就是具有单调性，所以在查找的时候，我们就可以用二分法来查找。
最后，注意本题的边界情况，当dp数组为空 或者 当前目标值大于dp数组里面的最大值时，我们直接将它插入到dp数组里即可，剩下的就只要用二分找到目的位置，进行修改即可。
代码：
class Solution {
public:
int LIS(vector<int>& a) {
vector<int> dp;
for(auto x : a)
{
if(!dp.size() || x > dp.back()) // 处理边界情况
{
dp.push_back(x);
}
else
{
int l = 0,r = dp.size() - 1;
while(l < r)
{
int mid = (r - l) / 2 + l;
if(dp[mid] >= x) r = mid;
else l = mid + 1;
}
dp[l] = x;
}
}
return dp.size();
}
};4.爱吃素
这题看似是让我们判断 a * b 是否是素数，如果我们直接判断的话，我们看到a和b的取值范围最大可以到 10^11，如果a b都取最大值，那么连long long都存不下的。
就算我们使用高精度来判断是否是素数，10^22 就算开根号，也是 10^11，这样的循环次数也是会超时的。
因此我们需要分析题目，用取巧的办法解决。
1.如果 a == 1 && b == 1，那么此时 a * b 就等于1，不是素数。
2.如果 a > 1 && b > 1，那么 a * b一定会有两个非1的因数，那么它一定是非素数。
3.如果 a == 1 && b是素数，或者 b == 1，a是素数，那么a * b也是素数。
代码：
#include <iostream>
#include <cmath>
using namespace std;
bool isPrime(long long x)
{
for(int i = 2; i < sqrt(x) + 1; ++i)
{
if(x % i == 0) return false;
}
return true;
}
int main()
{
int T;
cin >> T;
while(T--)
{
long long a,b;
cin >> a >> b;
if(a == 1 && b == 1)
cout << "NO" << endl;
else if(a > 1 && b > 1)
cout << "NO" << endl;
else if((a == 1 && isPrime(b)) || (b == 1 && isPrime(a)))
cout << "YES" << endl;
else
cout << "NO" << endl;
}
return 0;
}5.最长公共子序列（一）
这是一道dp的经典问题。
状态表示：
dp[i][j]：表示字符串s1中[0,i]区间以及字符串s2中[0,j]区间中，所有的子序列里面，最长的公共子序列长度。
状态转移方程：
1.s1[i] == s2[j]：那么此时我们就只需要从s1的[0,i - 1]和s2的[0,j - 1]中找到一个最长的公共子序列，然后 + 1进行拼接。
2.s1[i] != s2[j]：dp[i][j] = max(dp[i - 1][j],dp[i][j - 1])。
初始化：
给dp表多开一列和一行，方便填表。注意填表的时候i和j对应s1和s2中下标的映射关系。
代码：
#include <iostream>
#include <vector>
using namespace std;
int main()
{
int n,m;
cin >> n >> m;
string s1,s2;
cin >> s1 >> s2;
vector<vector<int>> dp(n + 1,vector<int>(m + 1));
for(int i = 1; i <= n; ++i)
{
for(int j = 1; j <= m; ++j)
{
if(s1[i - 1] == s2[j - 1])
dp[i][j] = dp[i - 1][j - 1] + 1;
else
dp[i][j] = max(dp[i - 1][j],dp[i][j - 1]);
}
}
cout << dp[n][m] << endl;
return 0;
}6.春游
解法：贪心 + 分情况讨论。
这里的贪心策略很简单：
先算出双人船和三人船它们平均载一个人需要多少钱，然后选择钱最少的即可。
但是这里的分情况讨论比较复杂，而且有陷阱：
当 3 * a <= 2 * b时，按照贪心策略，我们应尽可能选择双人船：
此时 ret += (n / 2) * a。当余数 tmp == 1时，这里其实是有三种方案的：
1.再选一条 a船。 价格：a
2.再选一条b船。价格 b
3.退掉一条a船，凑成三个人，再选择一条b船。价格：b - a。
所以ret += min(三种情况）
同理，当 3 * a > 2 * b时，我们尽可能选择三人船：
当余数 tmp == 1时，也有三种情况，
此时 ret += min(a,b,2 * a - b)，最后一个方案也就是退掉一条b船，再来两条a船。
当余数 tmp == 2时，同理:
ret += min(a,b, 3 * a - b)，最后一个方案是退掉一条b船，再来三条a船。
综合这些情况，写出代码：
#include <iostream>
using namespace std;
int T;
long long n,a,b;
long long Fun()
{
if(n <= 2) return min(a,b); // 边界情况
long long ret = 0;
int tmp;
if(3 * a <= 2 * b)
{
ret += a * (n / 2);
tmp = n % 2;
if(tmp == 1)
ret += min(a,min(b,b - a));
}
else
{
ret += b * (n / 3);
tmp = n % 3;
if(tmp == 1)
ret += min(a,min(b,2 * a - b));
else if(tmp == 2)
ret += min(a,min(b,3 * a - b));
}
return ret;
}
int main()
{
cin >> T;
while(T--)
{
cin >> n >> a >> b;
cout << Fun() << endl;
}
return 0;
}记得处理边界情况。
7.活动安排
这是一道区间贪心问题
解法：排序 + 贪心
我们按照左端点从小到大排好序后，然后就可以分情况讨论了。
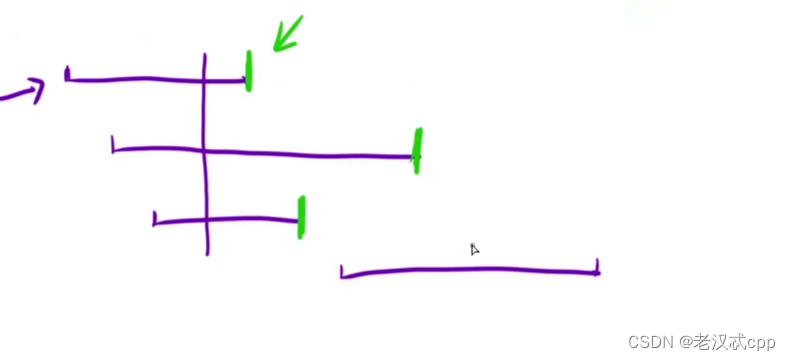如图四个区间，一开始ret里面固定放入一个值。接着每次循环遍历时，拿arr的左端点和ret.back()的右端点进行比较，如果小于了，说明就重叠了，那么我们就看看此时的ret的右端点是否要更新；否则就插入。
代码：
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int main()
{
int n;
cin >> n;
vector<pair<int,int>> arr(n);
for(int i = 0; i < n; ++i)
{
int a,b;
cin >> a >> b;
arr[i] = {a,b};
}
sort(arr.begin(),arr.end(),[](const pair<int,int>& p1,const pair<int,int>& p2){
return p1.first < p2.first;
});
vector<pair<int,int>> ret;
ret.push_back(arr[0]);
for(int i = 1; i < n; ++i)
{
auto[a,b] = arr[i];
auto[x,y] = ret.back();
if(a < y) // 重叠了
{
if(b < y) // 如果有更小的右端点就更新
{
ret.pop_back();
ret.push_back({a,b});
}
}
else
{
ret.push_back({a,b});
}
}
cout << ret.size() << endl;
return 0;
}8.合唱团
很难，是一道线性dp问题。
状态表示：
通常线性dp我们会想到i位置为结尾，的最大乘积。但是我们发现它有人数k和位置d的限制。所以dp[i]是满足不了的。
此时转化成二维dp，dp[i][j]表示前i个数，选j个人的最大乘积。但是因为还有位置d要求。所以我们设定dp[i][j]这个位置，i是必选的。 我们可以定义一个prev，来表示i - 1及之前的值。那么prev要满足 i - prev >= d -> prev >= i - d。另外还需要注意，prev 也必须大于等于 j - 1。
又因为测试数据有正有负，当数据是负的时候，在我们必选i位置的时候，如果要取得最大值，那么此时要从i - 1开始，往后合法个prev的区间中找到一个最小值，因此我们需要两个dp数组：
f[i][j] 表示以i位置为结尾并且必须选择arr[i]，在选择j个人的情况的最大值。
g[i][j] 表示以i位置为结尾，并且必须选择arr[i]，在选择j个人的情况下的最小值。
那么状态表示就分析出来了。
状态转移方程：
以f[i][j]为例，如果arr[i]是负数：
f[i][j] = g[prev][j - 1] * arr[i]。
如果arr[i]是正数：
f[i][j] = f[prev][j - 1] * arr[i]。
每次循环的时候二者取最大值。
那么g[i][j]的状态转移方程同理。
返回值：
因为最大值不一定是以n位置结尾的，所以我们在填表结束时，可以再遍历一遍f数组，取里面的最大值。
初始化：
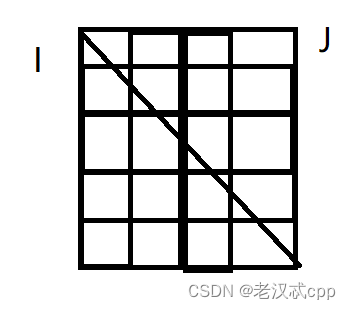
j是列，i是行。首先对角线以上的我们是不用管的，因为j是不可能比i要大的。另外，每行的第一列代表意思是从0到i位置，选择1个，又因为我们的dp表设计的是arr[i]是必选的，所以每行的第一列直接初始化为arr[i]即可。也就是dp[i][1] = arr[i]。
另外，以f[i][j]为例，其他的值都要初始化成负无穷，因为我们的最终结果也可能是负数，如果f[i][j]里面的其他值默认是0的话，那么就会干扰到每次比较的结果，使得结果不会为负数。g[i][j]也是同理，其余值要初始化为正无穷。
另外在循环的时候，我们已经每次都对每行的第一列进行了初始化，那么遍历的时候j要从2开始。
代码：
#include <iostream>
#include <vector>
using namespace std;
const int N = 0x3f3f3f3f; // 用它来代替正无穷
int main()
{
int n;
cin >> n;
vector<int> arr(n + 1);
for(int i = 1; i <= n; ++i)
cin >> arr[i];
int k,d;
cin >> k >> d;
vector<vector<long long>> f(n + 1,vector<long long>(k + 1,-N)); // 表最大值
vector<vector<long long>> g(n + 1,vector<long long>(k + 1,N)); // 表最小值
for(int i = 1; i <= n; ++i)
{
f[i][1] = g[i][1] = arr[i];
for(int j = 2; j <= min(i,k); ++j)
{
for(int prev = i - 1; prev >= max(i -d,j - 1); --prev)
{
f[i][j] = max(f[prev][j - 1] * arr[i],max(g[prev][j - 1] * arr[i],f[i][j]));
g[i][j] = min(g[prev][j - 1] * arr[i],min(f[prev][j - 1] * arr[i],g[i][j]));
}
}
}
long long ret = -N;
for(int i = k; i <= n; ++i) ret = max(ret,f[i][k]);
cout << ret << endl;
return 0;
}9.跳台阶扩展问题
这是青蛙跳台阶的进阶版。
解法一：动态规划
不过这里的dp时间复杂度是O(N^2)，因为青蛙每次可以选择条n阶台阶，所以还需要来一层循环。但是因为该题的数据量足够小，所以也可以过。
状态表示：
dp[i]表示跳i个台阶一共有几种跳法。
状态转移方程：
dp[i] += dp[i - 1] + dp[i - 2] + dp[i - 3] + ..... dp[0]。
初始化：
因为它可以跳n个台阶，所以除了将之前的跳法全加上之外，还要再加上一次就跳n台阶的方案，也就是加一。
代码：
#include <iostream>
using namespace std;
int dp[21];
int main()
{
int n;
cin >> n;
dp[0] = 0;
dp[1] = 1;
for(int i = 2; i <= n; ++i)
{
dp[i] = 1;
for(int j = i - 1; j >= 0; --j)
{
dp[i] += dp[j];
}
}
cout << dp[n] << endl;
return 0;
}解法二：找规律
我们可以拿dp的结果来查看规律
当n == 1时，结果： 1.
当n == 2时，结果：2
当 n == 3时，结果：4
当n == 4时，结果：8
当n == 5时，结果：16
到这里我们就发现规律了，我们只需要求 2 ^ (n - 1)即可。
代码：
#include <iostream>
using namespace std;
int main()
{
int n;
cin >> n;
int ret = 1;
for(int i = 1; i < n; ++i)
ret *= 2;
cout << ret << endl;
return 0;
}10.字符串的排列
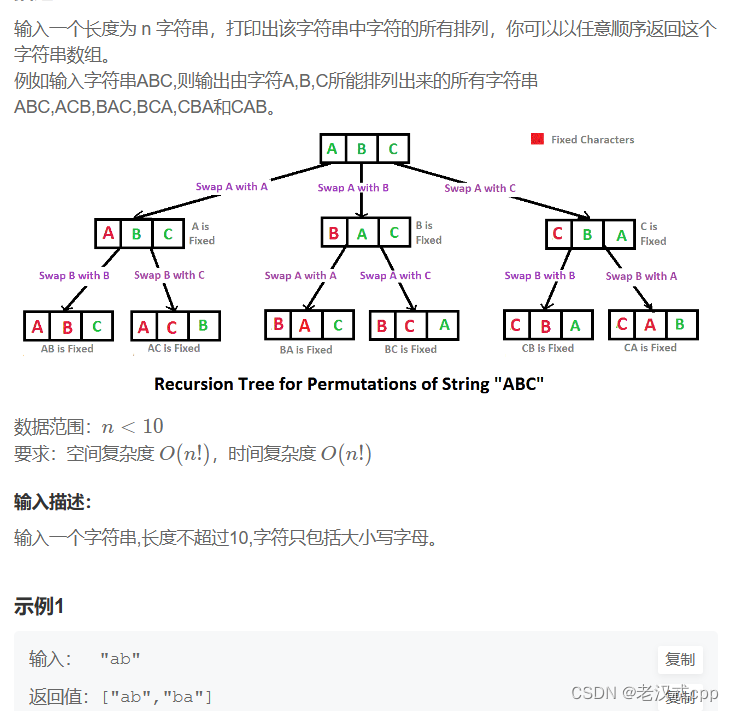解法：递归/dfs
这道题dfs的难点就是存在重复的字符，我们需要进行剪枝。
比如有 输入 "aba" ，如果不剪枝，那么结果就会出现 aab aab 这样的重复值。
解法：
先排序，将字符相同的放在一起
比如aba -> aab。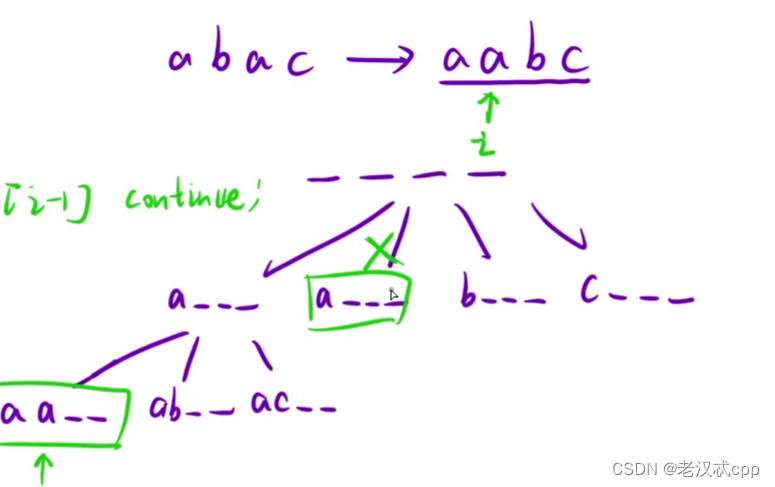
如果前一个字符和当前遍历的字符相同，并且前一个字符已经访问过了，那么就可以剪掉了。这样既保证了aab的出现，又保证了不会出现重复的aab。
就如上图。
代码：
class Solution {
public:
bool vis[11] = {0};
int n;
vector<string> ret;
string path;
string s;
vector<string> Permutation(string str) {
n = str.size();
s = str;
sort(s.begin(),s.end());
dfs(0);
return ret;
}
void dfs(int pos)
{
if(pos == n)
{
ret.push_back(path);
return;
}
for(int i = 0; i < n; ++i)
{
if(!vis[i]) // 访问过了肯定也要剪枝
{
if(i > 0 && s[i] == s[i - 1] && !vis[i - 1]) continue; //剪枝
path += s[i];
vis[i] = true;
dfs(pos + 1);
// 回溯
path.pop_back();
vis[i] = false;
}
}
}
};11.矩阵最长递增路径
这道题的解法可以从递归暴力搜索着手，然后通过记忆化搜索的方式优化。也称为带备忘录的动态规划。
暴力解法：
依次循环遍历矩阵，每遍历到一个点，就进入dfs依次暴力搜索，返回其中的最大值。
该题的数据范围是 0~1000，暴力搜索的话一般是会超时的。
优化：记忆化搜索：
思路其实很简单，创建一个备忘录，每次dfs完后，将该坐标遍历的结果保存起来，然后在每次dfs开始的时候，查看一下备忘录中这个坐标是否有有效值，如果有，那么就可以直接用。
代码：
class Solution {
int n,m;
int dx[4] = {0,0,-1,1};
int dy[4] = {1,-1,0,0};
int memo[1010][1010]; // 备忘录
public:
int solve(vector<vector<int> >& matrix) {
n = matrix.size();
m = matrix[0].size();
memset(memo,-1,sizeof(memo));
int ret = 1;
for(int i = 0; i < n; ++i)
{
for(int j = 0; j < m; ++j)
{
ret = max(ret,dfs(matrix,i,j));
}
}
return ret;
}
int dfs(vector<vector<int>>& matrix,int i,int j)
{
if(memo[i][j] != -1) return memo[i][j]; // 每次dfs前查看一下
int len = 1;
for(int k = 0; k < 4; ++k)
{
int x = i + dx[k];
int y = j + dy[k];
if(x >= 0 && x < n && y >= 0 && y < m && matrix[x][y] > matrix[i][j])
{
len = max(len,1 + dfs(matrix,x,y));
}
}
memo[i][j] = len; // 记得将结果保存到备忘录中
return len;
}
};12.计算字符串的编辑距离
这是一道经典的两个字符串之间的dp问题
状态表示：
dp[i][j] 表示字符串s1的[1,i]区间以及字符串s2[1,j]区间的编辑距离。
状态转移方程：
当s1[i] == s2[j]时：
dp[i][j] = dp[i - 1][j - 1]。（说明此时不需要修改，只需要继承之前的结果即可。）
当s1]i] != s2[j]时：
此时有三种情况：
1.s1[i]删除第i个字符来等于s2[j]，因为是删除了，所以变成了 s1 的[1,i - 1]区间到s2 的[1,j]区间的编辑距离。另外这是一次改动，所以要加上1。那么此时
dp[i][j] = dp[i - 1][j] + 1。
2.s1[i]增加一个字符来等于s2[j]。
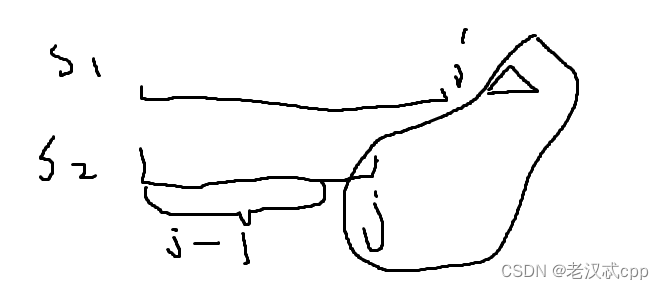
三角形表示s1新增的字符，使它等于s2的第j个字符。这也是一次改动，再继承之前的结果，那么
dp[i][j] = dp[i][j - 1] + 1。
3.改动 s1[i]使其等于s[j]。
根据前两次的分析，可得此时的
dp[i][j] = dp[i - 1][j - 1] + 1。
一共这三种情况，因为要尽可能的使改动次数少，所以取这三种的最小值。
初始化：
本题的初始化需要留心。除了要多开一行和多开一列来方便填表外，还需要考虑：
假设当i = 0时，说明s1是空字符串，那么此时要想让两个字符串相等，它的改动次数就是另一个字符串的长度。
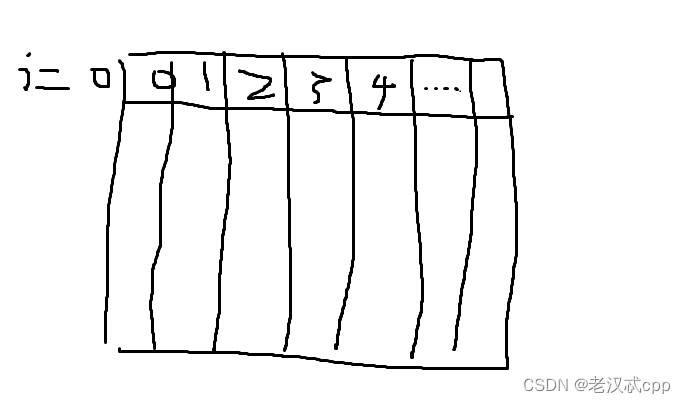
当j = 0时同理。
代码：
#include <iostream>
#include <vector>
using namespace std;
int main()
{
string s1,s2;
while(cin >> s1 >> s2)
{
int n = s1.size();
int m = s2.size();
vector<vector<int>> dp(n + 1,vector<int>(m + 1));
// 初始化
for(int i = 1; i <= n; ++i)
dp[i][0] = i;
for(int j = 1; j <= m; ++j)
dp[0][j] = j;
for(int i = 1; i <= n; ++i)
{
for(int j = 1; j <= m; ++j)
{
if(s1[i - 1] == s2[j - 1])
dp[i][j] = dp[i - 1][j - 1];
else
dp[i][j] = min(dp[i - 1][j],min(dp[i][j - 1],dp[i - 1][j - 1])) + 1;
}
}
cout << dp[n][m] << endl;
}
return 0;
}13.【模板】哈夫曼编码
如题目，就是考察哈夫曼编码的。这里只说应用。
简单了解：
一般我们存字符，比如abbccc，每一个字符用一个字节来存。但是如果我们用二进制来表示这些字符，就能够节省空间，达到压缩存储的效果。
要压缩存储，首先就要对每个字符进行编码和解码。比如编码：
假设有字符串 ‘abc’
我们将a设为0，b设为01， c设为001。
但是我们发现解码的时候就有问题了，比如001，我们究竟是解码成字符串ab还是字符串c呢？
哈夫曼编码就是为了解决这个问题的，也就是最优的压缩存储方式。
使用方法：
1.统计每个字符的出现频次。
2.根据频次建立最优二叉树。
以该题的例题为例，假设有字符串abbccc，那么它们出现的频次依次是 1 2 3（假设放到一个频次队列里面）。那么先取出值最小的两个最为二叉树的结点，形成了一颗二叉树，并将二者相加的结果放回到频次队列，此时队列的值就是 3 3。那么再取出这两个值，又组合成一颗二叉树，并将二者的值相加放回到队列里面，此时队列里面就只有一个值了，6，此时就结束了。这里其实是用到了贪心的思想。
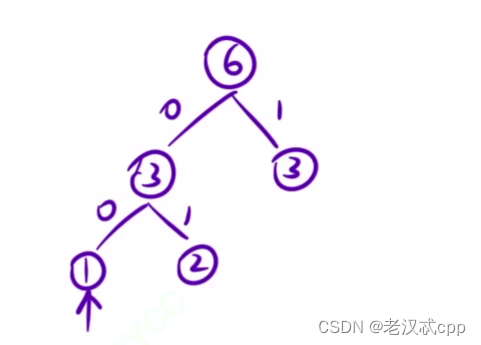
形成如上的最优二叉树。
并且要给每一条路径赋值，按照规律负0，1。
3. 根据最优二叉树
如上，最优二叉树建立好后，abbccc的编码 a：00 b：01，c：1。
那么根据频次乘上编码后的长度，总长度就是 1 * 2 + 2 * 2 + 3 * 1 = 9。所以最短长度就是9。
当然编码方式不唯一，比如我们将3放到左边，那么c的编码就是 1了，最短长度还是不变的。
最后再回到这道题，计算长度的方式有两种：
一：计算每个叶子结点到根结点的路径长度，也就是计算带权路径长度，但是这样比较麻烦，需要用到额外的数据结果。
二：我们可以在构建二叉树的时候，就记录结果。我们可以定于一个ret。每次取出两个结点的时候，就让ret += （两个结点的值）。最后直接返回即可。
那么此时我们就可以用到一个小根堆。在输入测试数据的时候，将数据放到小根堆里面。每次从堆顶取出两个元素，相加后再放回到堆里面。每次取出的时候记得pop。直到堆的大小等于1。
本题的测试用例的数值很大，记得用long long类型。
代码：
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
int main()
{
int n;
cin >> n;
vector<long long> arr(n);
priority_queue<long long ,vector<long long>,greater<long long>> heap;
for(int i = 0; i < n; ++i)
{
cin >> arr[i];
heap.push(arr[i]);
}
long long ret = 0;
while(heap.size() > 1)
{
long long t1 = heap.top();
heap.pop();
long long t2 = heap.top();
heap.pop();
ret += t1 + t2;
heap.push(t1 + t2);
}
cout << ret << endl;
return 0;
}14.abb
这道题有点难，这里采用动态规划的解法。
解法：动态规划 + 哈希表
状态表示：
dp[i] 表示以i元素位置为结尾的所有子序列中，有多少个 _xx。
返回值：
返回dp表中所有值的和。
状态转移方程（很绕）：
假设此时i位置元素的值是x，那么此时我们需要找到有多少个_x的序列即可，然后作相加。很显然，我们的dp表示无法找到 [0,i - 1]这个区间内有多少个 _x序列。所以此时我们可以定义一个哈希表(可以用数组表示)f。遍历到i时，f[x]表示 [0,i - 1]区间内有多少个 _x序列。这样 我们的状态转移方程：dp[i] = f[x]。
这样dp[i]更新完以后，我们就需要更新f[x]了，f[x]怎么 更新呢？既然f[x]在使用前表示的是[0,i - 1]区间有多少个_x序列，并且当前i位置元素就是字符x。那么我们只需要知道，在[0,i - 1]区间内，有多少个元素不是x，与i位置为结尾的x构成_x序列，并统计有多少个即可。
那么此时我们又需要一个哈希表g。g[x]在使用前表示，[0,i - 1]区间，有多少个x元素。然后用： （i - g[x]）的方式来表示有多少个非x的元素。用这些非x的元素与i位置的x元素组成_x序列。
这样的话f[x]的更新：f[x] = f[x] + i - g[x]。
最后，怎么更新g[x]呢？这个非常简单，因为g[x]表示[0,i - 1]内有多少个x元素，又因为i位置元素就是x，那么只要加1即可。所以g[x] = g[x] + 1。
到这里本题最难的地方就完了。
另外，我们发现dp表就是一个摆设，所以我们可以进行小小的空间优化，直接去掉dp表。因为本题只有小写字母，所以哈希表直接使用26个元素大小的数组即可。
还有要注意本题的数据范围，返回值和哈希表的类型建议使用long long类型。
代码：
#include <iostream>
using namespace std;
const int N = 1e5 + 10;
long long f[N] = {0};
long long g[N] = {0};
char s[N];
int main()
{
int n;
cin >> n >> s;
long long ret = 0;
for(int i = 0; i < n; ++i)
{
int x = s[i] - 'a';
ret += f[x];
f[x] = f[x] + i - g[x];
g[x] = g[x] + 1;
}
cout << ret << endl;
return 0;
}15.天使果冻
本题的白话就是找到到前x个数中的第二大的数。
解法：预处理 + 动规/递推
如果本题使用暴力解法，每次询问直接搜索前x个数，那么时间复杂度是O(n * q)的，大概率超时。
可以用数组g[i]表示前i个数中第二大的值。
但是要想表示第二大的数，我们还需要知道前i个数中最大的数是多少。所以还需要一个数组f[i]来表示前i个数中最大的数。
此时就可以分情况讨论了。
f[i]的更新很简单:f[i] = max(f[i - 1],arr[i])。
对于g[i]，如果arr[i] 有三种位置：
1.大于f[i - 1]，那么此时g[i] = f[i - 1]。
2.大于g[i - ]，小于f[i - 1]此时：g[i] = arr[i]。
3.小于g[i - 1]，此时：g[i] = g[i - 1]。
代码：
#include <iostream>
#include <vector>
using namespace std;
int main()
{
int n;
cin >> n;
vector<int> f(n + 1); // 前i个数中的最大值
vector<int> g(n + 1); // 前i个数中第二大的值
vector<int> arr(n + 1);
for(int i = 1; i <= n; ++i)
cin >> arr[i];
for(int i = 1; i <= n; ++i)
{
f[i] = max(f[i - 1],arr[i]);
if(arr[i] > g[i - 1] && arr[i] < f[i - 1])
g[i] = arr[i];
else if(arr[i] >= f[i - 1])
g[i] = f[i - 1];
else
g[i] = g[i - 1];
}
int q;
cin >> q;
while(q--)
{
int x;
cin >> x;
cout << g[x] << endl;
}
return 0;
}
16.小红取数
解法：动规（01背包问题） + 同余定理
这道题比较难，首先需要用到一个 同余定理
假设 a % k = x，b % k = y， 如果 （a + b）% k == 0，那么 （x + y）% k == 0反过来同样成立。
动规：
状态表示：如果直接用dp[i]表示从前i个数中挑选，总和是k的倍数的数，此时的和最大。我们发现状态转移方程是推不出来的。
所以要用二维的dp表。dp[i][j]，表示从前i个数中选，总和 % k == j时，最大是多少。
状态转移方程：
1.不选择arr[i]：dp[i][j] = dp[i - 1][j]。
2.选择arr[i]：此时要从[0,i - 1]中挑选，此时我们想让它的余数总和为j，所以我们就需要到 j - arr[i] % k中去挑选。所以此时转移方程：
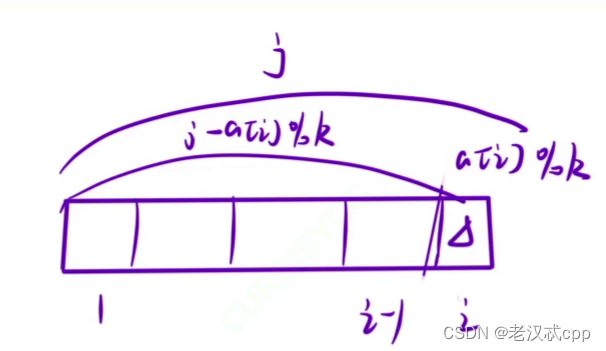
dp[i][j] = dp[i - 1][(j - arr[i] % k + k) % k]。
又因为 j - arr[i] % k 有可能为负数，所以我们在后面加上 k ，并为了不影响正数的情况，所以在外面加一个括号 % k。-> (j - arr[i] % k + k) % k。
每次遍历取二者的最大值。
返回值：
因为最大和得是k的倍数，也就是余数为0，所以返回dp[n][0]。
初始化：
第一列是不用管的，因为它表示的是当余数为0的情况，因为这些本来就是合法值，所以不用管。但是对于第一行，当i = 0时，余数0依然没问题，但是当余数是 1，2，3，.... k - 1时，是不合法的，因为我们在状态转移方程那里取的是最大值，所以为了让不合法的值不参与运算，所以我们可以将它们初始化成负无穷。
代码：
#include <iostream>
#include <cstring>
using namespace std;
const int N = 1010;
long long dp[N][N];
long long arr[N];
int main()
{
int n,k;
cin >> n >> k;
for(int i = 1; i <= n; ++i)
cin >> arr[i];
memset(dp,-0x3f3f3f3f,sizeof(dp));
dp[0][0] = 0;
for(int i = 1; i <= n; ++i)
{
for(int j = 0; j < k; ++j)
{
dp[i][j] = max(dp[i - 1][j],dp[i - 1][(j - arr[i] % k + k) % k] + arr[i]);
}
}
if(dp[n][0] <= 0) cout << - 1 << endl;
else cout << dp[n][0] << endl;
return 0;
}17.最少的完全平方数
错误解法：贪心。
这道题下意识会用贪心的解法来解决，比如n == 12时，我们先算出12之前的完全平方数，1，4，9。如果按贪心的算法来算，我们会选择9，1，1，1。会选择4次，但是其实只要选择3个4就可以了。所以贪心是不行的。
解法二：动规（完全背包问题）
这道题仔细看，就会发现很像完全背包问题。
状态表示：dp[i][j]表示在前i个数中，总和等于j的最少选择次数。
状态转移方程：
1.不选择arr[i]:dp[i][j] = dp[i - 1][j]。
2.选择arr[i]：因为是完全背包问题，所以arr[i]可以选择任意次数。
当选择1次时：dp[i - 1][j - i * i] + 1。
当选择2次时：dp[i - 1][j - 2 * i * i] + 2。
当选择3次时：dp[i - 1][j - 3 * i * i] + 3。
。。。
二者取最小值。
每次选择也是有限制的：j必须大于 n * （i * i）。
如果我们再搞一层循环来查询最优选择次数的话，时间复杂度会变成O(N ^ 3)，并且代码写起来也会变复杂。
我们用之前的规律可以得知：这些情况可以合并成 dp[i][j - i * i] + 1。
限制：j必须大于 i * i。
初始化：
多一行多一列。
dp[0][0]初始化为0。因为当数据的个数为0个数的时候，还要总和为1，2，3...是不合法的。所以需要给这些位置初始化为无效值，使它们不参与运算。 在状态转移方程中，我们取的是最小值，所以这里可以初始化成无穷大。
返回值：返回dp[sqrt(n),n]即可。
因为这里可以用空间优化，所以空间优化后返回dp[n]即可。
空间优化版本代码：
#include <iostream>
#include <vector>
using namespace std;
int main()
{
int n;
cin >> n;
vector<int> dp(n + 1,0x3f3f3f3f);
dp[0] = 0;
for(int i = 1; i * i <= n; ++i)
{
for(int j = i * i; j <= n; ++j)
{
dp[j] = min(dp[j],dp[j - i * i] + 1);
}
}
cout << dp[n] << endl;
return 0;
}18.游游的字母串
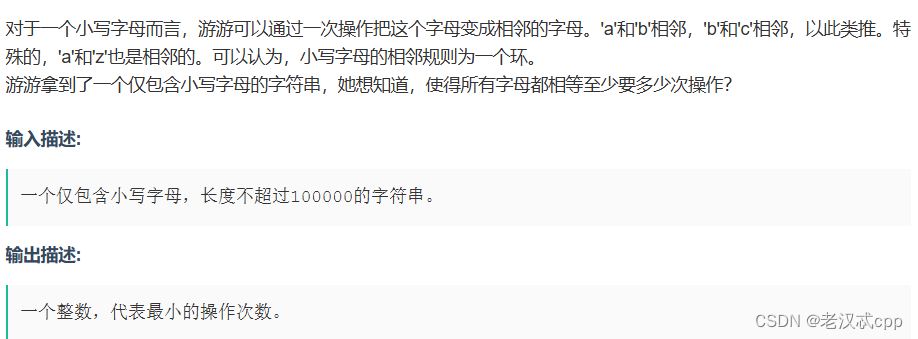
这道题很容易让人联想到各种解法，但是这道题直接用暴力解法即可。
我们直接使用arr[26]先来统计每个字母出现的次数，然后枚举a~z，选出其中最少的操作次数，那么时间复杂度也就是26n，也就是O(N)。
另外在枚举的时候，我们根据题意是知道，a到z是只需要操作一次的，所以我们在每次枚举统计本次枚举次数的时候，要注意：
正向操作次数： abs(a - s[j])。
反向操作次数：26 - abs(a - [s[j])。
每次相加取二者的最小值。
代码：
#include <iostream>
using namespace std;
int arr[26] = {0};
int main()
{
string s;
cin >> s;
int n = s.size();
for(int i = 0; i < n; ++i)
arr[s[i] - 'a']++;
int ret = 0x3f3f3f3f;
for(int i = 0; i < 26; ++i)
{
int count = 0;
char ch = i + 'a';
for(int j = 0; j < n; ++j)
{
count += min(abs(ch - s[j]),26 - abs(s[j] - ch));
}
ret = min(ret,count);
}
cout << ret << endl;
return 0;
}19.合唱队形
题意看起来很复杂，其实就是选身高，使身高队列满足先递增后递减，我们观察（1 <= i <= k)，也就是说纯递增或者纯递减都可以。
所以这就到了最长递增子序列和最长递减子序列问题了，我们直接用dp解决。
最长递增子序列：
状态表示：f[i]表示以i位置为结尾，最长的递增子序列的长度。
状态转移方程：
1.不选arr[i]： 1
2.选择arr[i]: 需要我们从 i - 1的位置开始往后遍历，如果arr[i] > arr[j] -> f[j] + 1。
二者取最大值,每次遍历取最大值
返回值：
一般的题目是要求最大值，但是我们只需要用到每个表中的值，所以不用记录最大值。
求递减最小子序列同理，我们可以对数组从后往前遍历，倒过来求最长递增自序列，等于求最长递减子序列。
20.宵暗的妖怪
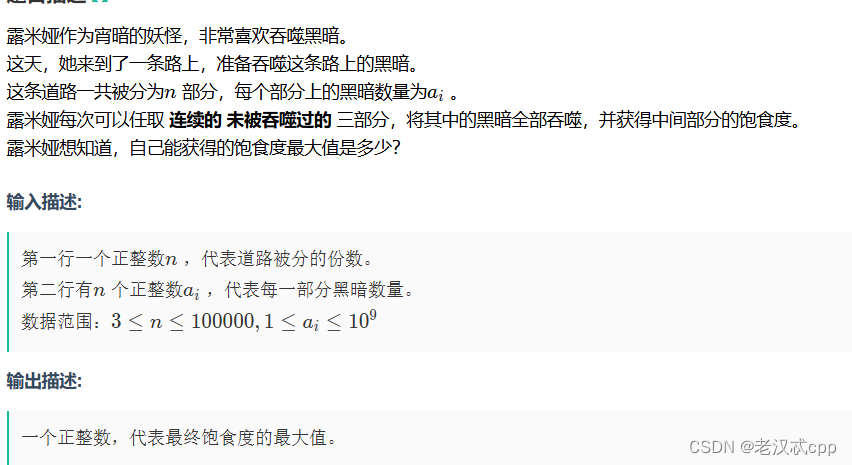
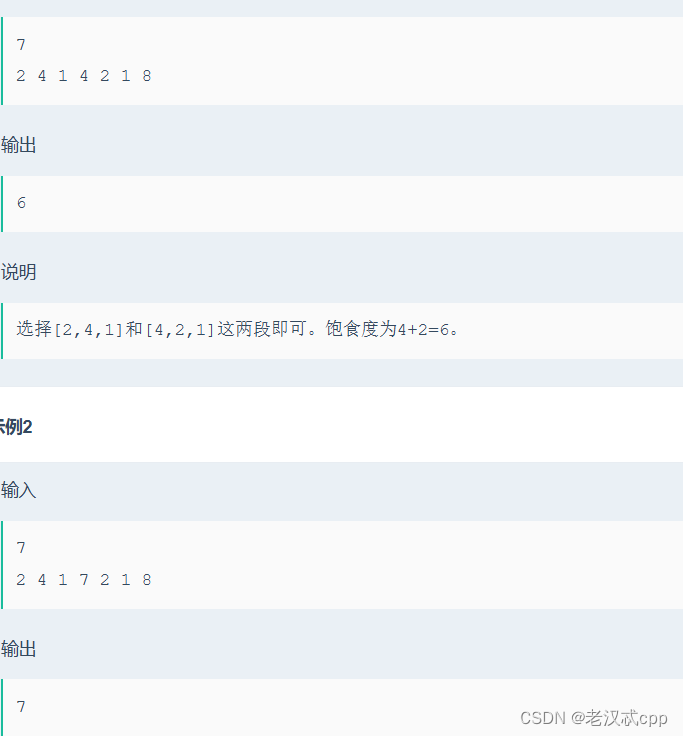
这是一道线性dp问题。
状态表示：
dp[i] 表示[1,i]区间，获得的饱食度的最大值。
状态转移方程：
1.选择arr[i]：dp[i - 3] + arr[i - 1]。
2.不选择arr[i]:直接从[1,i - 1]区间里面找，dp[i - 1]。
二者取最大值。
初始化：
因为至少得要三个连续的未被吞噬的黑暗才行，所以dp[1],dp[2]都得初始化为0。
代码：
#include <iostream>
using namespace std;
const int N = 1e5 + 10;
long long arr[N];
long long dp[N] = {0};
int main()
{
int n;
cin >> n;
for(int i = 1; i <= n; ++i)
cin >> arr[i];
for(int i = 3; i <= n; ++i)
{
dp[i] = max(dp[i - 3] + arr[i - 1],dp[i - 1]);
}
cout << dp[n] << endl;
return 0;
}21.过桥
本题解法：贪心 + bfs。
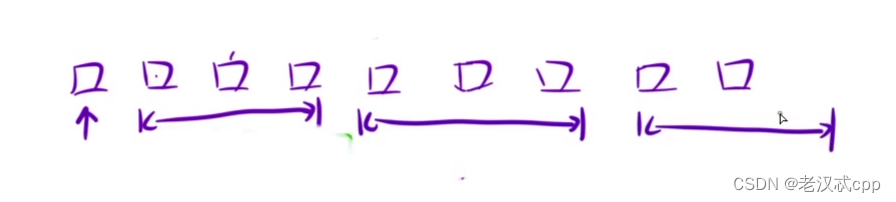对于每一个浮块，每一次起跳都有一个区间，假设最短可以跳到left，最远可以跳到right。
其实可以把它抽象成一个图论。
每次遍历的时候，我们要记录能遍历到的最远的位置，取每次 （arr[i] + i)的最大值。
然后将left更新成 right + 1，right 更新成r。
当right < left的时候，说明是没办法跳到n号浮块的。
代码：
#include <iostream>
using namespace std;
int n;
const int N = 2e3 + 10;
int arr[N] = {0};
int dfs()
{
int ret = 0;
int left = 1,right = 1;
while(left <= right)
{
int r = right;
++ret;
for(int i = left; i <= right; ++i)
{
r = max(r,i + arr[i]);
if(r >= n) return ret;
}
left = right + 1;
right = r;
}
return -1;
}
int main()
{
cin >> n;
for(int i = 1; i <= n; ++i)
cin >> arr[i];
cout << dfs() << endl;
return 0;
}22.最大差值
这道题要先读懂题意，它的要求是 0 <= a <= b < n 。求A[b] - A[a]的最大值，也就是说，是数组后面的某个数减去前面的某个数（可以是同一个位置），取相减的最大值。
解法：贪心 + 模拟
暴力枚举自不用多说，两层for循环，O(N^2)的时间复杂度，面对题中的测试用例大概率超时。
贪心就是我们在遍历数组的同时，将i位置以前的最小值保留下来，prevmin，并且每次遍历开始就先执行min（prevmin，A[i]），然后取每次 A[i] - prevmin的最大值。
代码：
int getDis(vector<int>& A, int n) {
int ret = 0;
int prevmin = A[0];
for(int i = 0; i < n; ++i)
{
prevmin = min(prevmin,A[i]);
ret = max(ret,A[i] - prevmin);
}
return ret;
}23.兑换零钱
这是一道典型的动态规划中的完全背包问题。在这里当作复习了。
因为它的每种货币可以重复选择，所以是完全背包问题。
状态表示：
dp[i][j] : 从前i个货币中选， 使价值正好等于j所需要的最少货币。
状态转移方程：
1.不选：dp[i - 1][j]。
2.选n个：
这里就是完全背包的特色之处
选1个：dp[i - 1][j - arr[i]] + 1。
选2个：dp[i - 1][j - 2 * arr[i]] + 2。
选 n个.....
但是我们可以把这些情况总和为dp[i][j - arr[i]] + 1。
选两种情况的最小值。
初始化：
这也是重要的一环。第一列不用管，因为后面也会处理的。对于第一行：就是没有货币的情况凑成价值j。当j == 0的时候，直接初始化为0。当j > 0 时，因为没有货币，所以无论如何也凑不出价值j。所以要初始化成不会干扰后续填表的值。这里可以初始化成无穷大（用0x3f3f3f3f代替）。
返回值：
返回dp[n][aim]。因为存在无解的情况，所以需要先判断dp[n][aim]是否为无穷大，是就返回-1，否则正常返回。
关于空间优化：
去掉原本的行，在填表的时候，j那里依旧从左往右填。
返回dp[aim]，同样记得要判断一下。
代码：（无空间优化）
#include <iostream>
#include <cstring>
using namespace std;
const int N = 1e4 + 10;
const int M = 5010;
int arr[N] = {0};
int dp[N][M] = {0};
int main()
{
int n,aim;
cin >> n >> aim;
for(int i = 1; i <= n; ++i)
cin >> arr[i];
memset(dp,0x3f3f3f3f,sizeof(dp));
dp[0][0] = 0;
for(int i = 1; i <= n; ++i)
{
for(int j = 0; j <= aim; ++j)
{
dp[i][j] = dp[i - 1][j];
if(j >= arr[i])
dp[i][j] = min(dp[i][j],dp[i][j - arr[i]] + 1);
}
}
if(dp[n][aim] == 0x3f3f3f3f) cout << -1 << endl;
else cout << dp[n][aim] << endl;
return 0;
}空间优化：
#include <iostream>
#include <cstring>
using namespace std;
const int N = 1e4 + 10;
const int M = 5010;
int arr[N] = {0};
int dp[M] = {0};
int main()
{
int n,aim;
cin >> n >> aim;
for(int i = 1; i <= n; ++i)
cin >> arr[i];
memset(dp,0x3f3f3f3f,sizeof(dp));
dp[0] = 0;
for(int i = 1; i <= n; ++i)
{
for(int j = arr[i]; j <= aim; ++j)
{
dp[j] = min(dp[j],dp[j - arr[i]] + 1);
}
}
if(dp[aim] == 0x3f3f3f3f) cout << -1 << endl;
else cout << dp[aim] << endl;
return 0;
}24.小红的子串
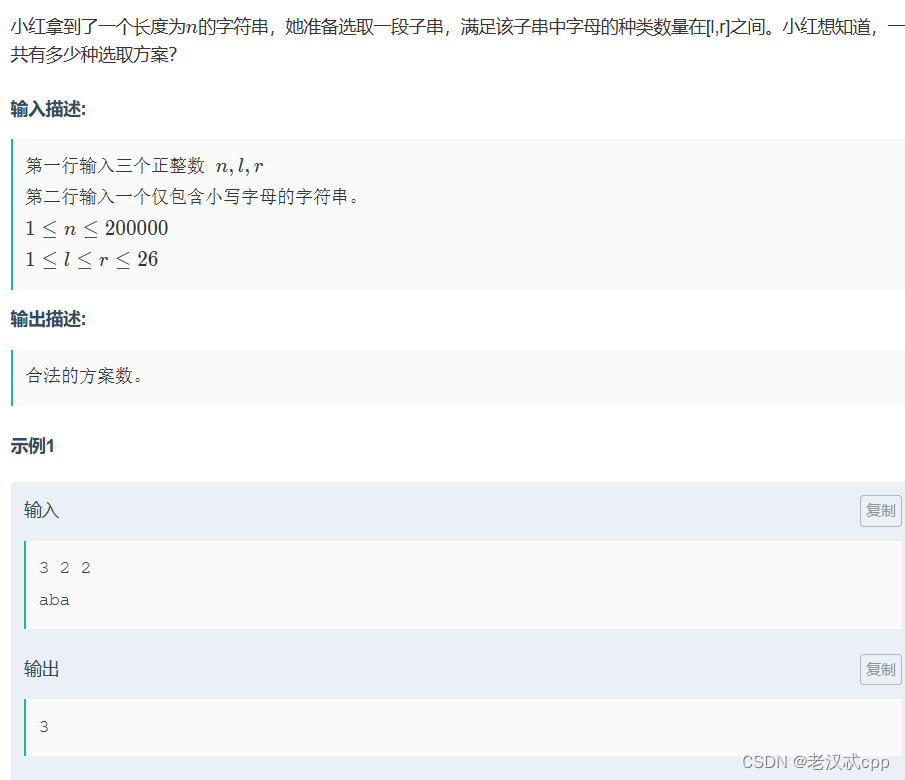本题解法：滑动窗口 + 前缀和
这里的前缀和只是小用一下思想。
如果直接找比如字符串种类在[2,3]区间类的字符串的话，最差的时间复杂度是O(N^2)的，大概率超时。
我们可以先找到[1,1]区间的字符串数量ret1，再找到[1,3]区间的字符串数量ret2。然后用ret2 - ret1就可以得出[2,3]的字符串数量的，每次查找用滑动窗口的思想只需要O(N)的时间复杂度。
用两遍就可以得出结果。
代码：
#include <iostream>
using namespace std;
int n,l,r;
string s;
long long fun(int x)
{
if(x == 0) return 0; // 特殊情况
int kinds = 0;
int left = 0;
int right = 0;
long long ret = 0;
int hash[26] = {0};
while(right < n)
{
if(hash[s[right] - 'a']++ == 0) kinds++;
while(kinds > x)
{
if(hash[s[left] - 'a']-- == 1) kinds--;
left++;
}
ret += right - left + 1;
right++;
}
return ret;
}
int main()
{
cin >> n >> l >> r;
cin >> s;
cout << fun(r) - fun(l - 1) << endl;
return 0;
}
25.kotori和抽卡（二）
看起来是很简单的一道题，主要考察的是概率论期望的知识。更多的是考验代码能力
公式：
代码：
#include <iostream>
#include <stdio.h>
using namespace std;
int main()
{
int n,m;
cin >> n >> m;
double ret = 1.0;
for(int i = n; i >= n - m + 1; --i) ret *= i; // 计算分子
for(int i = m; i >= 2; --i) ret /= i;// 计算分母
// 然后计算概率
for(int i = 0; i < m; ++i) ret *= 0.8;
for(int i = 0; i < n - m; ++i) ret *= 0.2;
printf("%.4f",ret);
return 0;
}26.ruby和薯条
解法：排序 + 滑动窗口 + 前缀和
在排完序后，我们其实只需要找到[0,l - 1]区间的对数x和[0,r]区间的对数y。
然后y - x 就是我们的最终结果。
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
int n,l,r;
//统计[0,r]区间的对数
long long find(vector<int>& nums,int r)
{
int left = 0,right = 0;
long long ret = 0;
while(right < n)
{
while(nums[right] - nums[left] > r) left++;
ret += right - left;
right++;
}
return ret;
}
int main()
{
cin >> n >> l >> r;
vector<int> nums(n);
for(int i = 0; i < n; ++i)
cin >> nums[i];
sort(nums.begin(),nums.end());
cout << (find(nums,r) - find(nums,l - 1)) << endl;
return 0;
}27.循环汉诺塔
这道题简单来说就是汉诺塔，但是每次移动只能是顺时针移动，比如原版的汉诺塔可以从A直接移动到C，这道题的汉诺塔只能是这样的移动顺序：
A->B, B->C, C->A。这样的循环顺时针的移动方式。
这道题的数据量很大，所以肯定不能用递归，重点在于寻找子问题。
我们可以从n = 1开始寻找规律
当我们模拟到n = 3时，就能发现规律并找到子问题了，假设上一次A->B所需要的次数是x，A->C的次数是y，那么这一次A->B的次数就是 2y + 1，A->的次数就是 2y + 2 + x。
找到规律后就很好写代码了。
#include <iostream>
using namespace std;
int const N = 1000000007;
int main()
{
int n;
cin >> n;
long long x = 1,y = 2;
for(int i = 1; i < n; ++i)
{
long long a = x,b = y;
x = (2 * b + 1) % N;
y = (2 * b + a + 2) % N;
}
cout << x << " " << y << endl;
return 0;
}28.kotori和素因子
题意简单来说就是给若干个正整数，从每个整数中找到一个合适的素因子，使得这些素因子的和最小。
我们看到数据量大概能猜出要用暴力枚举的方式解决。dfs。
那么我们同样可以先描绘决策树
所以这道题其实比较考察代码能力。
我们需要设计判断素数，设计递归函数，还需要剪枝。
代码：
#include <iostream>
#include <cmath>
using namespace std;
const int N = 15,M = 1010;
int n;
int arr[N];
bool vis[M];
int path = 0;
int ret = 0x3f3f3f3f;
bool isPrim(int x)
{
if(x <= 1) return false;
for(int i = 2; i <= sqrt(x); ++i)
{
if(x % i == 0) return false;
}
return true;
}
void dfs(int pos)
{
if(pos == n)
{
ret = min(ret,path);
return;
}
for(int i = 2; i <= arr[pos]; ++i)
{
if(arr[pos] % i == 0 && !vis[i] && isPrim(i))
{
vis[i] = true;
path += i;
dfs(pos + 1);
vis[i] = false;
path -= i;
}
}
}
int main()
{
cin >> n;
for(int i = 0; i < n; ++i)
cin >> arr[i];
dfs(0);
if(ret == 0x3f3f3f3f) cout << -1 << endl;
else cout << ret << endl;
return 0;
}29.dd爱科学1.0
题意简单来说就是修改字符串中的元素，使得字符串呈非递减序列，每次修改花费代价1，求最小花费是多少。
其实我们可以求出最长的非递减子序列，然后用总长度减去这个长度就可以得出我们所花费的最小代价。
那么问题就变成了求最长非递减子序列问题了。
这种问题跟求：
递增
递减
非递增
非递减
这类问题是一模一样的。
解法有两种：1.动态规划。时间复杂度是O(N^2)本题会超时
2.贪心 + 二分查找 时间复杂度是O(N * logN)。
所以用方法二。
那么解决这个问题，我们只需要关心末尾字符是什么就可以了，然后用二分查找找到合适的位置修改这个字符。
另外还有边界问题，如果新来的字符大于目前最长的字符串的末尾，那么我们直接将它插到末尾，并将长度 + 1。
代码：
#include <iostream>
using namespace std;
const int N = 1e6 + 10;
char dp[N]; // dp[i] 表示长度为i的所有子序列中，最小的末尾是什么
string s;
int main()
{
int n;
cin >> n >> s;
int len = 0;
for(int i = 0; i < n; ++i)
{
// 注意边界问题
if(len == 0 || s[i] >= dp[len])
{
dp[++len] = s[i];
}
else
{
int left = 0,right = len;
while(left < right)
{
int mid =left + (right - left) / 2;
if(dp[mid] <= s[i]) left = mid + 1;
else right = mid;
}
dp[left] = s[i];
}
}
cout << (n - len) << endl;
return 0;
}
30.拜访
简单来说就是单源最短路径的扩展，需要我们求出最短方案有多少种。
所以加上原来的数组一共有三个数组，dist记录步数，判断是否走过，还能判断是否是最短路径，cnt数组的作用是表示到cnt[i][j]这个位置的最短路径方案有多少种。
代码：
int countPath(vector<vector<int> >& CityMap, int n, int m) {
int ret = 0;
int minstep = INT_MAX;
vector<vector<int>> vis(n,(vector<int>(m,-1)));
vector<vector<int>> cnt(n,(vector<int>(m,0)));
queue<pair<int,int>>q;
int x1,y1; // 记录商家位置用的
for(int i = 0; i < n; i++)
{
for(int j = 0; j < m; ++j)
{
if(CityMap[i][j] == 1)
{
q.push({i,j});
vis[i][j] = 0;
cnt[i][j] = 1; // 记得初始化
}
if(CityMap[i][j] == 2)
{
x1 = i;
y1 = j; // 记录一下终点位置
}
}
}
int dx[4] = {0,0,-1,1};
int dy[4] = {1,-1,0,0};
while(q.size())
{
auto [a,b] = q.front();
q.pop();
for(int i = 0; i < 4; ++i)
{
int x = a + dx[i];
int y = b + dy[i];
if(x >= 0 && x < n && y >= 0 && y < m && CityMap[x][y] != -1)
{
// 第一次到这个位置
if(vis[x][y] == -1)
{
vis[x][y] = vis[a][b] + 1;
q.push({x,y});
cnt[x][y] += cnt[a][b];
}
else
{
// 先判断是否是最短路径
if(vis[a][b] + 1 == vis[x][y])
{
cnt[x][y] += cnt[a][b];
}
}
}
}
}
return cnt[x1][y1];
}31.买卖股票的最好时机(四)
这是买卖股票的终极问题，同时如果学会该道题，类似的题就能用通用的解法解决。
解法：动规，是线性dp。
常规的状态表示比如dp[i]是满足不了本题的。
本题存在两种状态：1.手里有股票的状态。2.手里没有股票的状态。
所以需要两个状态表示，f[i]表示手里有股票的状态。g[i]表示手里没有股票的状态。
另外有交易次数的限制，所以最终的状态表示为：
1.f[i][j]表示手里有股票，此时交易次数为j，此时的最大利润。
2.g[i][j]同理推出。
状态转移方程：
先看状态机图：
可以看到两种状态之间转换的条件，那么可以推导出状态转移方程
另外需要注意，在g[i][j]时，要避免数组越界问题。
初始化：
要为了不影响填表的目的去初始化。
两张表都多开一行和多开一列方便填表。
注意在f表中，第0天交易0次的时候，应该是-p[0]。其余第0天的都初始化为负无穷。
那么在g表中，第0天交易0次的时候，值应该是0，其余同理。
返回值：
当手里有股票时，此时利润肯定不是最大。所以我们应该从g表中寻找结果，并且应该从最后一天也就是最后一行中寻找最大值并返回。
另外关于交易次数k的值有一个小细节，有些题目会将k的值给的很大，但其实我们最大的交易次数只能是n / 2次，所以我们可以先将k的值处理一下，相当于小优化。
代码：
#include <iostream>
#include <vector>
using namespace std;
int main()
{
int n,k;
cin >> n >> k;
vector<int> nums(n);
for(int i = 0; i < n; ++i)
cin >> nums[i];
k = min(k,n / 2); // 细节，小优化
vector<vector<int>> f(n + 1,(vector<int>(k + 1,-0x3f3f3f3f))); // 卖出的状态
vector<vector<int>> g(n + 1,(vector<int>(k + 1))); // 买入的状态
f[0][0] = -nums[0];
for(int i = 1; i <= n; ++i)
{
for(int j = 0; j <= k; ++j)
{
f[i][j] = f[i - 1][j];
f[i][j] = max(f[i][j],g[i - 1][j] - nums[i - 1]);
g[i][j] = g[i - 1][j];
if(j >= 1)
g[i][j] = max(g[i][j],f[i - 1][j - 1] + nums[i - 1]);
}
}
int ret = 0;
for(int j = 0; j <= k; ++j)
ret = max(ret,g[n][j]);
cout << ret << endl;
return 0;
}
6622
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
