求解反常积分的特殊方法（一）

伏如兰尼积分

        我们称形如

                           

        的积分为伏如兰尼积分。

        设函数在上连续，且时，函数具有有限的极限，即

                                                   

        那么，我们就可以得到伏如兰尼公式，即

                                

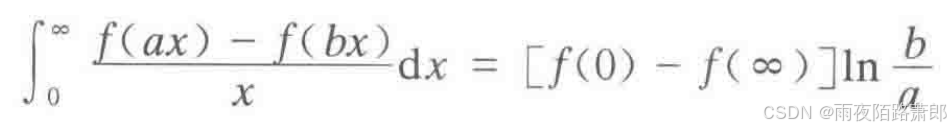
        伏如兰尼公式的证明需要推广的中值定理的知识，在这里我们不做详细证明。该公式主要针对反常积分的求解问题，常用于选择题与填空题。我们下面举几个典型的例子，来更加深刻地理解与应用该公式。

                        ​​​​​​​        

        ​​​​​​​        ​​​​​​​        ​​​​​​​        

        ​​​​​​​        ​​​​​​​        ​​​​​​​        

        下面我们使用伏如兰尼积分来求解上面三道反常积分。

        第一题就是非常规范与明显的伏如兰尼积分公式，我们直接套公式，可得

                                

        原积分式子的结果即

                                 

        第二道题就需要进行变换来凑成伏如兰尼积分，只需要多算一步分部积分法，即

                    

        第三道就比较综合了，需要通过换元来进行配凑，使原积分变成伏如兰尼积分。我们先观察原积分的上下限，发现其不符合伏如兰尼积分的上下限，故我们应当对其进行换元，使得换元后所得的积分式子上下限符合伏如兰尼积分的要求。进一步观察，原积分的被积函数分母是对数函数，对其进行求原函数也不太简单，再者我们知道

                                     

       因此我们可以令

                     

                     

      于是我们就有

        ​​​​​​​        ​​​​​​​    

      这样子就可以使用伏如兰尼积分进行计算了。上述三道典型例题主要是让大家对于伏如兰尼积分的应用有更深的理解，便于后面的学习与进步。