【二】【算法】P1008 [NOIP1998 普及组] 三连击，P1003 [NOIP2011 提高组] 铺地毯，P1002 [NOIP2002 普及组] 过河卒

P1008 [NOIP1998 普及组] 三连击

[NOIP1998 普及组] 三连击

题目背景

本题为提交答案题，您可以写程序或手算在本机上算出答案后，直接提交答案文本，也可提交答案生成程序。

题目描述

将 $1,2,\dots ,9$ 共 $9$ 个数分成 $3$ 组，分别组成 $3$ 个三位数，且使这 $3$ 个三位数构成 $1:2:3$ 的比例，试求出所有满足条件的 $3$ 个三位数。

输入格式

无

输出格式

若干行，每行 $3$ 个数字。按照每行第 $1$ 个数字升序排列。

样例 #1

样例输入 #1

无

样例输出 #1

* * * ...

* * * （剩余部分不予展示） ```

## 提示

NOIP1998 普及组 第一题

代码

#include<iostream>
#include<bits/stdc++.h>
using namespace std;
int main(){
    int a[10];
    for(int i=123;i<=333;i++){
        a[1]=i/100;
        a[2]=i/10%10;
        a[3]=i%10;
        a[4]=2*i/100;
        a[5]=2*i/10%10;
        a[6]=2*i%10;
        a[7]=3*i/100;
        a[8]=3*i/10%10;
        a[9]=3*i%10;

        if(a[1]*a[2]*a[3]*a[4]*a[5]*a[6]*a[7]*a[8]*a[9]==(1*2*3*4*5*6*7*8*9)&&a[1]+a[2]+a[3]+a[4]+a[5]+a[6]+a[7]+a[8]+a[9]==(1+2+3+4+5+6+7+8+9))
            cout<<i<<" "<<2*i<<" "<<3*i<<endl;
    }
}

• 已知条件
  对于三个三位数,假设为a,b,c,已知条件是a2=b,a3=c,并且a b c中所有数字只出现一次.
• 初步思路
  因此我们可以模拟数字a,数字b和c可以通过等式b=2a,c=3a得出.
• 判断独立数字为1,2,3,4,5,6,7,8,9
  如何判断所有数字只出现一次?取出这三个三位数所有的独立数字,如果满足条件必须这九个数字是1,2,3,4,5,6,7,8,9.
  取出的所有数字依次相乘,相加判断与1,2,3,4,5,6,7,8,9数字依次相乘相加是否一致.

P1003 [NOIP2011 提高组] 铺地毯

[NOIP2011 提高组] 铺地毯

题目描述

为了准备一个独特的颁奖典礼，组织者在会场的一片矩形区域（可看做是平面直角坐标系的第一象限）铺上一些矩形地毯。一共有 $n$ 张地毯，编号从$1$ 到 $n$。现在将这些地毯按照编号从小到大的顺序平行于坐标轴先后铺设，后铺的地毯覆盖在前面已经铺好的地毯之上。

地毯铺设完成后，组织者想知道覆盖地面某个点的最上面的那张地毯的编号。注意：在矩形地毯边界和四个顶点上的点也算被地毯覆盖。

输入格式

输入共 $n+2$ 行。

第一行，一个整数 $n$，表示总共有 $n$ 张地毯。

接下来的 $n$ 行中，第 $i+1$ 行表示编号 $i$ 的地毯的信息，包含四个整数 $a,b,g,k$，每两个整数之间用一个空格隔开，分别表示铺设地毯的左下角的坐标 $(a,b)$ 以及地毯在 $x$ 轴和 $y$ 轴方向的长度。

第 $n+2$ 行包含两个整数 $x$ 和 $y$，表示所求的地面的点的坐标 $(x,y)$。

输出格式

输出共 $1$ 行，一个整数，表示所求的地毯的编号；若此处没有被地毯覆盖则输出 -1。

样例 #1

样例输入 #1

3 1 0 2 3 0 2 3 3 2 1 3 3 2 2

样例输出 #1

3

样例 #2

样例输入 #2

3 1 0 2 3 0 2 3 3 2 1 3 3 4 5

样例输出 #2

-1 

提示

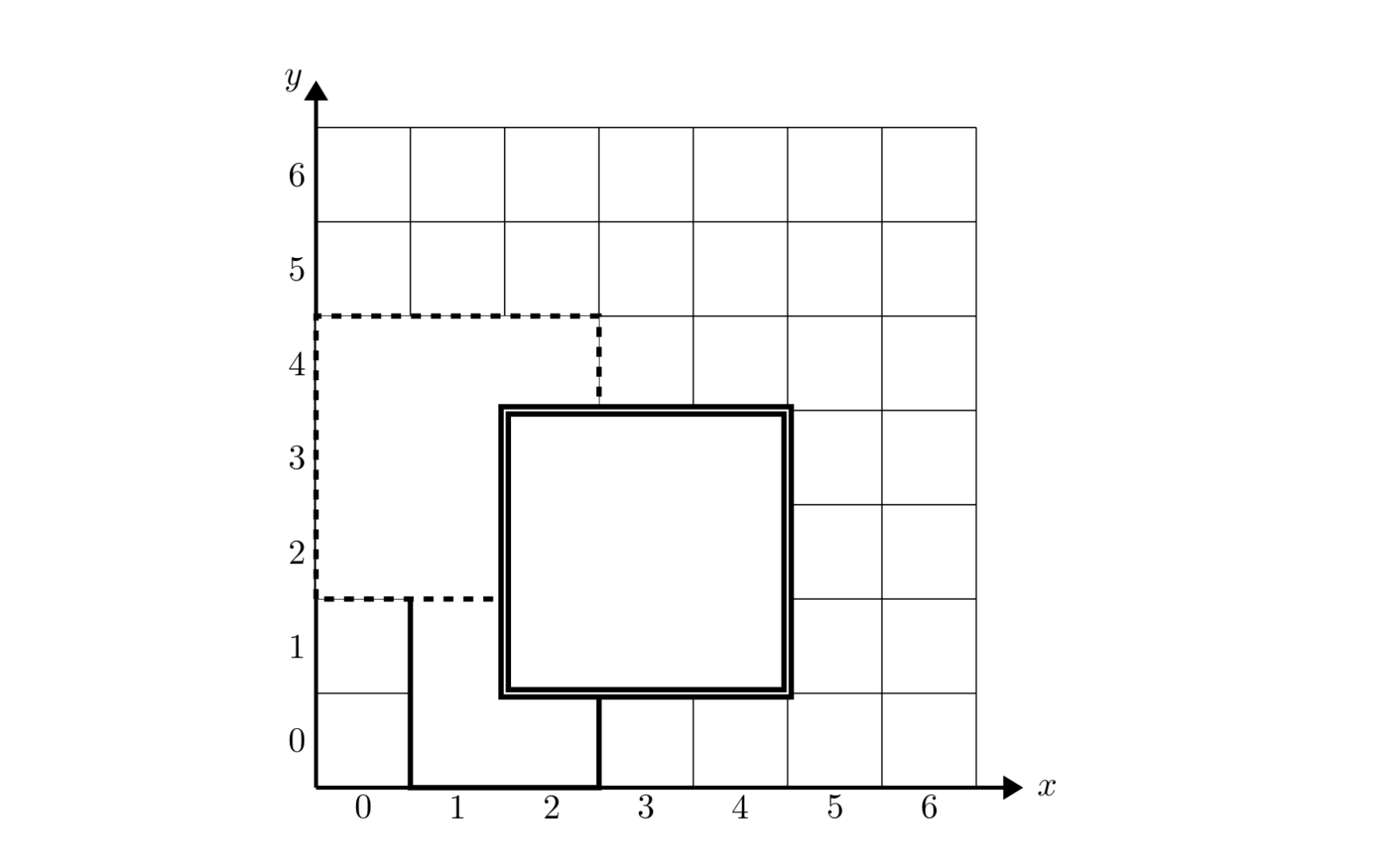
【样例解释 1】

如下图，$1$ 号地毯用实线表示，$2$ 号地毯用虚线表示，$3$ 号用双实线表示，覆盖点 $(2,2)$ 的最上面一张地毯是 $3$号地毯。

【数据范围】

对于 $30\%$ 的数据，有 $n\le 2$。 对于 $50\%$ 的数据，$0\le a,b,g,k\le 100$。
对于 $100\%$ 的数据，有 $0\le n\le 10^4$, $0\le a,b,g,k\le {10}^5$。

noip2011 提高组 day1 第 $1$ 题。

代码

#include<bits/stdc++.h>
using namespace std;


struct node {
	int a, b, g, k;
};
int main() {
	int n;
	cin >> n;
	vector<node>read;
	for (int i = 0; i < n; i++) {
		int a, b, g, k;
		cin >> a >> b >> g >> k;
		read.push_back({ a,b,g,k });
	}
	int x, y;
	cin >> x >> y;

	int ret=-1;
	int i = 1;
	for (auto pos : read) {
		int a, b, g, k;
		a = pos.a; b = pos.b; g = pos.g; k = pos.k;
		int x1 = a; int x2 = a + g;	int y1 = b;	int y2 = b + k;
		if (x <= x2 && x >= x1 && y >= y1 && y <= y2) ret = i;
		i++;
	}

	cout << ret << endl;
	return 0;

}

• 题目要求
  我们需要判断在x,y点上最后一次铺上地毯的地毯编号,如果x,y坐标上没有被铺上地毯,则输出-1.
• 思路
  因此我们可以先得到x,y点,每一次铺地毯时我们判断x,y点是否在这次地毯上,如果被地毯覆盖了就记录一次地毯的编号.
• 存储输入数据
  因为我们是先输入地毯的数据然后再输入目标点x,y坐标.因此我们可以先用一个变量存储先输入的地毯数据,也就是说我们可以用变量存储所有的需要输入的数据,然后再统一使用.

P1002 [NOIP2002 普及组] 过河卒

[NOIP2002 普及组] 过河卒

题目描述

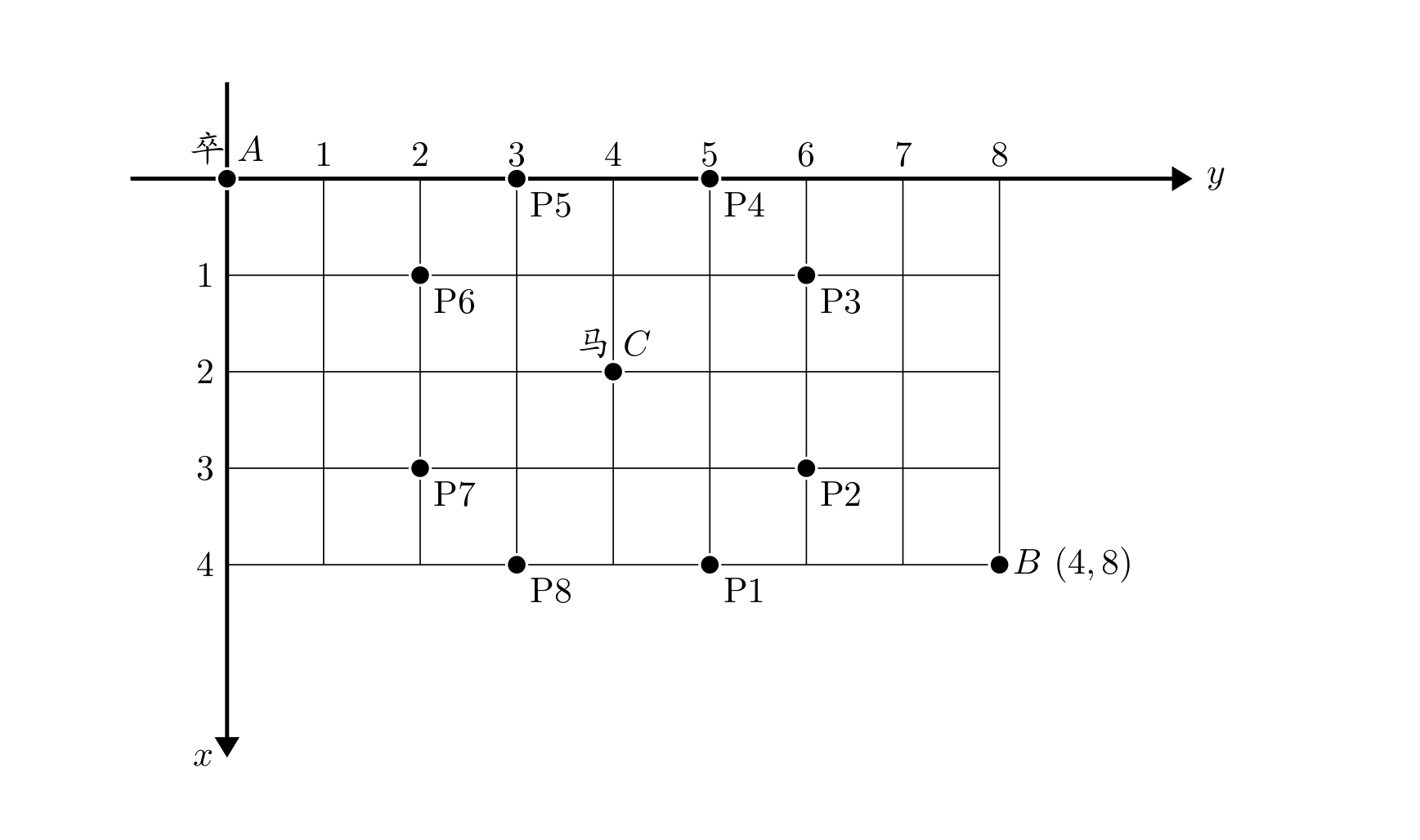
棋盘上 $A$ 点有一个过河卒，需要走到目标 $B$ 点。卒行走的规则：可以向下、或者向右。同时在棋盘上 $C$ 点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。

棋盘用坐标表示，$A$ 点 $(0,0)$、$B$ 点 $(n,m)$，同样马的位置坐标是需要给出的。

现在要求你计算出卒从 $A$ 点能够到达 $B$ 点的路径的条数，假设马的位置是固定不动的，并不是卒走一步马走一步。

输入格式

一行四个正整数，分别表示 $B$ 点坐标和马的坐标。

输出格式

一个整数，表示所有的路径条数。

样例 #1

样例输入 #1

6 6 3 3

样例输出 #1

6

提示

对于 $100\%$ 的数据，$1\le n,m\le 20$，$0\le$ 马的坐标 $\le 20$。

【题目来源】

NOIP 2002 普及组第四题

代码

#if 1
#include "bits/stdc++.h"
using namespace std;
using ll = long long;
int main() {
	ll endx, endy;
	cin >> endx >> endy;
	ll x0, y0;
	cin >> x0 >> y0;

	vector<pair<ll, ll>> forbit_pos;
	forbit_pos.push_back({ x0 + 1,y0 + 2 });
	forbit_pos.push_back({ x0 + 1,y0 - 2 });
	forbit_pos.push_back({ x0 + 2,y0 + 1 });
	forbit_pos.push_back({ x0 + 2,y0 - 1 });
	forbit_pos.push_back({ x0 - 1,y0 + 2 });
	forbit_pos.push_back({ x0 - 1,y0 - 2 });
	forbit_pos.push_back({ x0 - 2,y0 + 1 });
	forbit_pos.push_back({ x0 - 2,y0 - 1 });
	forbit_pos.push_back({ x0 ,y0 });

	vector<vector<ll>> dp = vector<vector<ll>>(endx + 1, vector<ll>(endy + 1, 0));
	dp[0][0] = 1;

	for (auto pos : forbit_pos) {
		int x = pos.first;
		int y = pos.second;
		if (x >= 0 && x <= endx && y >= 0 && y <= endy) {
			dp[x][y] = -1;
		}
	}

	if (dp[0][0] == -1) {
		cout << 0 << endl; return 0;
	}

	for (int i = 0; i <= endx; i++) {
		for (int j = 0; j <= endy; j++) {
			if (i == 0 && j == 0) continue;
			if (dp[i][j] == -1)continue;
			dp[i][j] = ((i - 1 >= 0 && dp[i - 1][j] != -1) ? dp[i - 1][j] : 0) + ((j - 1 >= 0 && dp[i][j - 1] != -1) ? dp[i][j - 1] : 0);
		}
	}

	cout << dp[endx][endy] << endl;

}
#endif

• 思路
  很明显的动态规划题目,创建对应大小的二维dp数组,0~endx,0~endy,所以需要开辟endx+1和endy+1个空间,如果不想思考太多可以统一开辟endx+3,endy+3个空间.
• 数据的存储
  用forbit_pos记录所有的禁止的点坐标,分别是以马坐标为基准的马脚点,注意不要忘记了马本身也是一个禁止点.
• 注意事项
  不要忘记了特殊判断,比如说当我们的起始点0,0位置如果是禁止点那么我们直接输出0即可.

结尾

最后，感谢您阅读我的文章，希望这些内容能够对您有所启发和帮助。如果您有任何问题或想要分享您的观点，请随时在评论区留言。
同时，不要忘记订阅我的博客以获取更多有趣的内容。在未来的文章中，我将继续探讨这个话题的不同方面，为您呈现更多深度和见解。
谢谢您的支持，期待与您在下一篇文章中再次相遇！