树形dp——换根dp

endlessdream01

已于 2023-11-25 15:59:26 修改

阅读量186

点赞数

分类专栏：动态规划dp 文章标签：算法动态规划 c++

于 2023-11-23 22:22:54 首次发布

本文链接：https://blog.csdn.net/m0_74176921/article/details/134586736

版权

动态规划dp 专栏收录该内容

8 篇文章 0 订阅

订阅专栏

引入 STA-Station

首先我们先看这样一道例题，根据我们之前学的树形dp基础，于是我们有如下做法

我们假设某个节点为根，将无根树化为有根树，在搜索dfs统计子树的深度和，则可以用一次搜索算出以该节点为根时的深度和，其时间复杂度为 $O(n)$ 。

但这样求解出的答案只是以该节点为根的，并不是最优解。

如果要暴力求解出最优解，则我们可以枚举所有的节点为根，然后分别跑一次搜索，这样的时间复杂度会达到 $O(n^2)$ ，显然不可接受。

于是我们引入今天的换根 $dp$

换根dp

什么是换根dp呢，如其名，就是将不是根的换成根，也就是把该树的子节点变成根。

我们先定义 $dp[u]$ 表示以u为根的所有子节点的深度之和。

我们注意到，如果我们求出了某个 $dp[root]$ ，其中 $root$ 表示该树的根，那么对于 $root$ 的任意一个孩子节点child, $dp[child]$ 是可以通过O（1）时间求出来的。换根之后有什么变化，为什么可以通过O(1)求出呢，我们通过一个图更加清晰的理解。

如图，我们的根节点就是0，接下来我们选取子节点2作为新的根节点，对其进行换根

接下来我们来看一下有哪些变化，很明显的变化就是有地方下沉了，也就是深度减小了。

通过观察，我们发现，右边的深度减少了，左边的增加了，减少的节点为未换根之前以0为根节点经过2的所有路径上的节点，增加的为没有经过2的。且增减度为1。

于是我们有如下（num[i]表示以i为根的子树包含的总节点数量）

$dp[child]=dp[root] - num[child] + (n - num[child])$

其中

$num[child]$ 表示以child为根节点的节点总数，因为顺着child往下的子节点的深度会减少1，于是 $- num[child]$ 就表示深度的减少量

$n - num[child]$ 就表示为上升的深度，不经过child的子节点树都增加，不经过的节点数目就是从节点数目减去经过的节点数目。

代码实现

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
typedef long long ll;//开ll 会爆
const int N=1e6+10;
ll e[N*2],ne[N*2],dp[N];int h[N],idx;
int dep[N],sum[N];//dep[u],表示u节点的深度，usm[u]表示节点数
int n;

void add(int a,int b)
{
	e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}


//先跑出以u为根节点的深度总和
void dfs(int u,int fa)
{
	dep[u]=dep[fa]+1;//u是往父节点下去的，于是深度就比父节点大1
	sum[u]=1;//最开始只有u自己这个节点
	for(int i=h[u];i!=-1;i=ne[i])
	{
		int v=e[i];
		if(v==fa)continue;
		dfs(v,u);
		sum[u]+=sum[v];
	}
}

//利用换根
void dfs2(int u,int fa)
{
	for(int i=h[u];i!=-1;i=ne[i])
	{
		int v=e[i];
		if(v==fa)continue;
		dp[v]=dp[u]+n-2*sum[v];//u是父节点，v是要换根的子节点不要对用错了
		dfs2(v,u);
	}
}

int main()
{
	memset(h,-1,sizeof h);
	cin>>n;
	for(int i=1;i<n;i++)
	{
		int a,b;cin>>a>>b;
		add(a,b),add(b,a);
	}
	dfs(1,0);
	for(int i=1;i<=n;i++)
		dp[1]+=dep[i];//初始化dp[1]
	dfs2(1,0);
	ll ans=0,p=0;//p记录哪个节点最大
	for(int i=1;i<=n;i++)
		if(ans<dp[i])
			ans=dp[i],p=i;
			
	cout<<p<<"\n";
	return 0;	
}

例题

1Choosing Capital for Treeland

分析

本题的意思就是给一个有向树，求树上哪个节点到其他所有点需要重新建反向边的边数最少。题中出现了哪个节点，要对这个信息敏感，很可能是换根dp。我们可以先任选一个节点当作根节点（这里我选择了节点1），然后遍历dfs，求出 $f[1]$ ，即节点1到其他所有点需要重新建反向边的边数。

注意题目这里说的是单向边，而且需要反向建边的操作，我们想一下是都还可以建双向边

于是不妨设正向边的权重为0，表示可以直接通行不需要建边，

设反向边的权值为1，表示不能直接通行，需要建边，设置了权值，当我们走了这条边就相当于反向建这条边这个过程。

于是我们可以通过跑一遍dfs，得到了以u为根节点所需要建立的反向边的数量。

接下来我们对其进行换根处理。我们先思考一下换根之后之后的变化与什么有关，当然题目问的是反向边，自然与反向边有关了。

接下来我们考虑两种情况，首先是根节点u能到达要换根的v号节点，也就是不需要建立反向边，如下图，其中红色表示根节点，蓝色表示要换根的节点

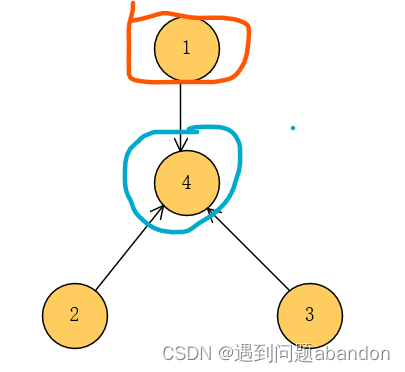
此时需要建立一条4到2和4到3的边才能符合题意，接下来我们看一下换根之后的变化

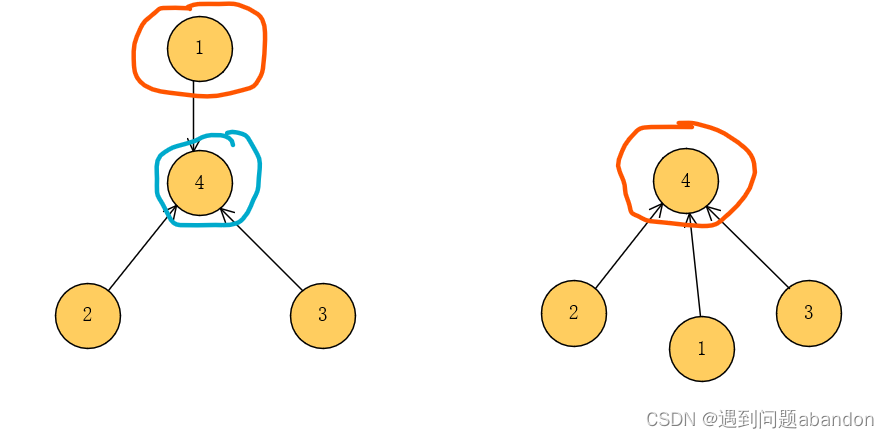
我们会发现，原本1能到4，但是换根之后，也就是1沉下去之后反而不能到达了，于是我们需要建立多建立一条边，这时候是4到2，4到1，4到3

于是我们便有了我们换根后的第一个状态转移，假设u为根节点，为预要换根的节点

$f[v]=f[u]+1$ $(u\rightarrow v)$

接下来我们分析另外一种情况，根节点u不能到达要换根的v号节点，也就是需要建立反向边

相同于上述方法，我们分析可得到

$f[v]=f[u]-1$ $(v\rightarrow u)$

代码

//f[u]表示以u为根节点，需要建立的反向边的数量
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
typedef long long ll;
const int N=2e5+10;
ll e[N*2],ne[N*2],w[N*2];
int h[N],idx;
int f[N],ans=1e9;

void add(int a,int b,int c)
{
	e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}

//先进行第一遍遍历，找出以u为根所需要建立的反向边的条数
void dfs(int u,int fa)
{
	for(int i=h[u];i!=-1;i=ne[i])
	{
		int v=e[i];
		if(v==fa)continue;
		dfs(v,u);
		f[u]+=(f[v]+w[i]);
		
	}
}

//进行换根操作
void dfs2(int u,int fa)
{
	for(int i=h[u];i!=-1;i=ne[i])
	{
		int v=e[i];
		if(v==fa)continue;
		if(w[i])//有反向边的时候也就是v->u
			f[v]=f[u]-1;
		else//u->v
			f[v]=f[u]+1;
		dfs2(v,u);
	}
}

int main()
{
	memset(h,-1,sizeof h);
	int n;cin>>n;
	for(int i=1;i<n;i++)
	{
		int a,b;cin>>a>>b;
		add(a,b,0),add(b,a,1);//正向边的权值为0，需要建立的反向边权值为1
	}
	dfs(1,0);
	int res=f[1];
	dfs2(1,0);
	for(int i=1;i<=n;i++)
		ans=min(ans,f[i]);
	cout<<ans<<"\n";
	for(int i=1;i<=n;i++)
		if(ans==f[i])
		cout<<i<<" ";
	return 0;
}

2 Great Cow Gathering G

就不做分析了，参考上面，只是多了个点权和边权

代码

//设f[u]表示以u为根，所有奶牛走过来的距离之和
//f[u]=f[v]+size[v]*w[i];
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=1e6+10;
typedef long long ll;
ll e[N*2],ne[N*2],cnt[N],sum;//cnt[u]表示u的子节点加起来一共有多少头牛
ll w[N],h[N],idx;
ll s[N],f[N];
int n;

void add(int a,int b,int c)
{
	e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}

void dfs(int u,int fa)
{
	cnt[u]=s[u];//先初始化只有自己节点的牛
	for(int i=h[u];i!=-1;i=ne[i])
	{
		int v=e[i];
		if(v==fa)continue;
		dfs(v,u);
		cnt[u]+=cnt[v];
		f[u]+=f[v]+w[i]*cnt[v];
		//cout<<f[u]<<"  ";
	}
}
//换根
void dfs2(int u,int fa)
{
	for(int i=h[u];i!=-1;i=ne[i])
	{
		int v=e[i];
		if(v==fa)continue;
		f[v]=f[u]+(sum-2*cnt[v])*w[i];
		dfs2(v,u);
	}
}


int main()
{
	memset(h,-1,sizeof h);
	cin>>n;
	for(int i=1;i<=n;i++)
		cin>>s[i],sum+=s[i];
	for(int i=1;i<n;i++)
	{
		int a,b,c;cin>>a>>b>>c;
		add(a,b,c),add(b,a,c);
	}
	dfs(1,0);
	dfs2(1,0);
	ll ans=1e18;//此题数据挺歹毒的，不要开小了
	for(int i=1;i<=n;i++)
		ans=min(ans,f[i]);
		
	cout<<ans;
	return 0;
}

3 Nearby Cows G

分析

题目要求我们求的是，对于每个节点求出距离它不超过 k 的所有节点权值和

既然是求距离小于等于k的点权和，那我们便可以依次把 $0-k$ 的每一个距离的点权都给算出来，最后再相加即可。于是我们便可以定义我们的状态方程为， $f[u][k]$ 表示为距离节点u距离为k的点权。

至于更新方式，那就是经过了子节点v的和没经过子节点的相加即可， $f[u][j]=f[u][j]+f[v][j-1]$ ,v节点的j的减一，这是因为，u到v已经走了一格，v再往下就只能走j-1了，加起来才能是j，然后我们通过一遍dfs，跑出了 $f[u][0],f[u][1]....f[u][k]$

接下来就要考虑换根了，下面我们演示k=3时的换根，看看有那些变化

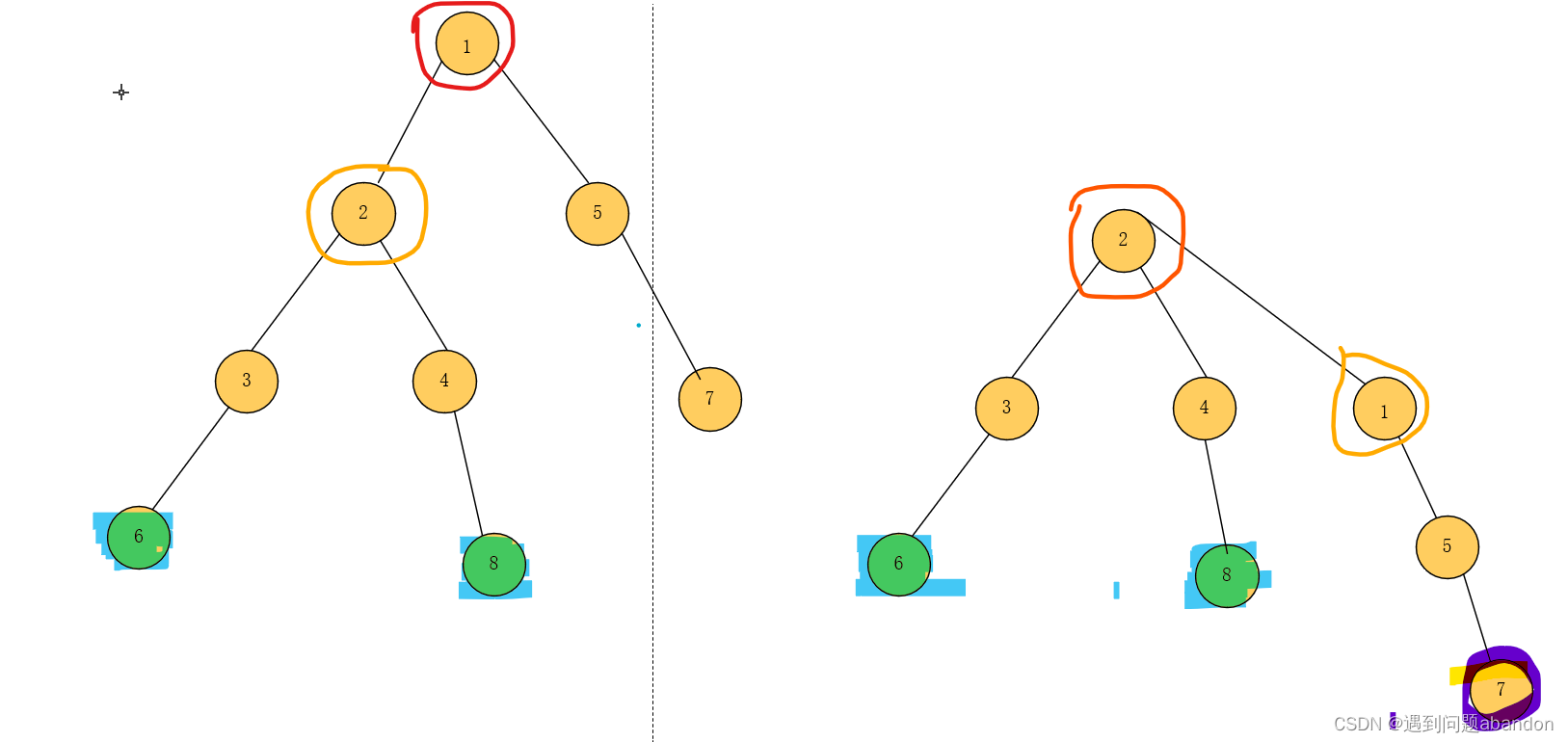
于是我们发现，再1为根节点的时候，蓝色部分是满足条件k=3的，但是换根之后，反而不满足以2为根了，这是因为换根之后，左边都经过v(这里等于2)往下的节点，都降低了，然后对于节点7，再根为1的时候是满足k=2的，但是由于右边没有经过v,所以他的长度上升了，所以可以加入到我们换根之后满足k=3的节点中。于是我们知道是需要加上 $f[u][j-1]$ 的。

如上图，当我们加上 $f[u][j-1]$ 的时候，还加上了一些我们不需要的，如3和4，这时候我们要想办法把他去掉，在根为 $u$ 的时候，这些节点是 $k=j-1$ 的情况，于是在根为 $v$ 的时候，自然就是 $k=j-2$ 了,于是我们再减去 $f[v][j-2]$ ,我们此时又突然发现，我们好像把1号节点，也就是我们原来的根 $u$ 不小心也给剪掉了，因为是跟3和4处于同一层。但是这个情况指挥出现在更新 $f[v][1]$ 的情况跟下出现，于是我们需要在最后 $f[v][1]$ 上加上 $w[u]$ 即可。

代码

//定义f[u][i]表示以u为根节点，距离u的距离为i的点权之和
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
typedef long long ll;
const int N=1e5+10;
ll e[N*2],ne[N*2],f[N][25];//
int h[N],idx,w[N];//点权值
int n,k;

void add(int a,int b)
{
	e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}


void dfs(int u,int fa)
{
	f[u][0]=w[u];//距离为0就是本身
	for(int i=h[u];i!=-1;i=ne[i])
	{
		int v=e[i];
		if(v==fa)continue;
		dfs(v,u);//从子节点推到父节点
		for(int j=1;j<=k;j++)
			f[u][j]+=f[v][j-1];
	}
}

//换根
void dfs2(int u,int fa)
{
	for(int i=h[u];i!=-1;i=ne[i])
	{
		int v=e[i];
		if(v==fa)continue;
		for(int j=k;j>=2;j--)//采用逆序更新，从大的先来，从小的会被覆盖
			f[v][j]+=f[u][j-1]-f[v][j-2];
		f[v][1]+=w[u];
		dfs2(v,u);
	}
}

int main()
{
	memset(h,-1,sizeof h);
	cin>>n>>k;
	for(int i=1;i<n;i++)
	{
		int a,b;cin>>a>>b;
		add(a,b),add(b,a);
	}
	for(int i=1;i<=n;i++)
		cin>>w[i];
		
	dfs(1,0);
	dfs2(1,0);
	for(int i = 1; i <= n; i++)
    {
        ll ans = 0;
        for(int j = 0; j <= k; j++)
        ans += f[i][j];
        cout << ans << endl;
    }

	return 0;
}

4.Maximum White Subtree

分析

题目的大致意思是，给定一棵 n个节点无根树，每个节点 u有一个颜色，若颜色为 0 则表示u是黑点，若为 1 则表示u是白点。因为颜色白色是1，对我们的树有贡献，黑色是0，对我们的树没有贡献，所以我们需要求白色点的个数减去黑色点的个数 cnt1−cnt2 的最大值。

由于黑色点是没有贡献，他存在就会使得我们的结果变小，于是我们假设从某节点出发，遇黑-1，遇白+1。

假设 u 为根节点， v 为一个子节点，于是我们有如下状态转移

$dp[u]=dp[u]+dp[v]>0?dp[v]:0$ 这表示总根 u 的获得的总贡献值等于，从子节点 v 往下的贡献值，加上不经过子节点 v 的贡献值。对于负的贡献值显然我们不需要把他计入其内。

于是我们通过跑一遍 dfs 便得出了我们想要的根节点 u 的贡献值，接下来我们来进行换根

蓝色的表示有有贡献值，红色的表示没有，画了黄圈的表示答案

我们考虑 v 及其子树是否对 u 有贡献，如果有贡献，如上下图，为3和4，我们现在把根 u 换下去了，自然3和4不能成为成为其子树，所以此时 $dp[u]$ 应该减去 $dp[v]$ ，对于新根 $dp[v]$ 的计算方法，现在 u 是其子树了，那自然要加上 $dp[u]$ (加了几个点，不理解可以看一下10和11这里)

代码

//定义状态f[u]表示以u为根节点的最大值
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
typedef long long ll;
const int N=2e5+10;
ll e[N*2],ne[N*2];
int h[N],idx,a[N],f[N];
int n;

void add(int a,int b)
{
	e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}

void dfs(int u,int fa)
{
	f[u]=(a[u]==1?1:-1);
	for(int i=h[u];i!=-1;i=ne[i])
	{
		int v=e[i];
		if(v==fa)continue;
		dfs(v,u);//由子节点更新到父节点，所以要先dfs找到叶子节点
		f[u]+=(f[v]>0?f[v]:0);//大于0才往上面更新
	}
}

//换根
void dfs2(int u,int fa)
{
	for(int i=h[u];i!=-1;i=ne[i])
	{
		int v=e[i];
		if(v==fa)continue;
		int x=f[u],y=f[v];//需要先用临时变量储存起来
		if(y>0)x-=y;
		if(x>0)y+=x;//有贡献的时候才加进来
		f[v]=y;
		dfs2(v,u);
	}
}

int main()
{
	memset(h,-1,sizeof h);
	cin>>n;
	for(int i=1;i<=n;i++)
		cin>>a[i];
	for(int i=1;i<n;i++)
	{
		int a,b;cin>>a>>b;
		add(a,b),add(b,a);
	}
	dfs(1,0);
	dfs2(1,0);
	for(int i=1;i<=n;i++)
		cout<<f[i]<<" ";
	return 0;
}

endlessdream01

关注

0
点赞
踩
0

收藏

觉得还不错? 一键收藏
0
评论
树形dp——换根dp

通过观察，我们发现，右边的深度减少了，左边的增加了，减少的节点为未换根之前以0为根节点经过2的所有路径上的节点，增加的为没有经过2的。我们假设某个节点为根，将无根树化为有根树，在搜索dfs统计子树的深度和，则可以用一次搜索算出以该节点为根时的深度和，其时间复杂度为。就表示为上升的深度，不经过child的子节点树都增加，不经过的节点数目就是从节点数目减去经过的节点数目。如图，我们的根节点就是0，接下来我们选取子节点2作为新的根节点，对其进行换根。但这样求解出的答案只是以该节点为根的，并不是最优解。
复制链接

扫一扫