【离散数学】九章：关系 - 关系的表示

本节及本章的剩余部分研究的所有关系均为二元关系，因此，在这些内容中出现的“关系〞一词都表示二元关系

1、用集合表示关系

关系是序偶的集合，所以描述集合能用的方法一般都可以描述关系，比如枚举满足关系的所有序偶，比如叙述满足关系的性质。

前面的例子都是用集合表示关系，这里不赘述

2、用矩阵表示关系

矩阵表示关系

有限集之间的关系可用0-1 矩阵表示：

假设 R 是从 A = { a₁, a₂，…，a_m } 到 B = { b₁, b₂，…，b_n } 的关系，则A×B上的所有关系可以用一个 m×n的长方形 0-1 矩阵 来表示。

关系R由矩阵 M_R = [ m_ij ] 表示，其中

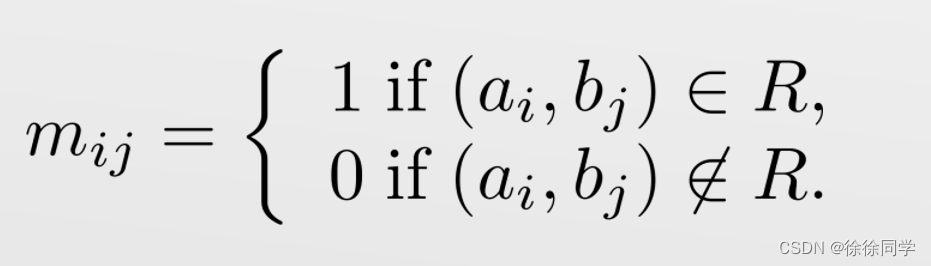
当 a_i 与 b_j 相关时，表示 R 的 0-1 矩阵的 (i, j) 项是1，如果a_i 与 b_j 无关系，则是0

📘例1：
假设 A = { 1, 2, 3 }，B = { 1, 2 }。令 R 为 A 到 B 的关系，如果 a∈A，b∈B 且 a > b，则 R 包含 (a, b)。表示 R 的矩阵是什么（假设元素的顺序与递增的数值顺序相同）？

由题意得，R = { (2, 1), (3, 1), (3, 2) }，因此矩阵为：

📘例2：
设 A = { a₁, a₂, a₃ }，B = { b₁, b₂, b₃, b₄, b₅ }。哪些有序对在下面的矩阵所表示的关系 R 中？

因为 R 是由 m_ij = 1 的有序对 (a_i, b_j) 构成的，所以
R = { (a₁, b₂), (a₂, b₁), (a₂, b₃), (a₂, b₄), (a₃, b₁), (a₃, b₃), (a₃, b₅) }

⭐集合上的关系矩阵

表示定义在一个集合上的关系的矩阵是一个方阵，可以用这个矩阵确定关系是否有某种性质

R 自反时

R 是自反的，当且仅当 M_R 的主对角线上的所有元素都等于1
❗ 注意：非主对角线上的元素可以是 0 或 1

R 对称时

R 是对称关系，当且仅当 若m_ij = 1 则 m_ji = 1

换句话说：R 是对称关系，当且仅当 M_R = (M_R)^T

（沿主对角线对称）

R 反对称时

R 是反对称关系，当且仅当 i ≠ j 时，m_ij = 0 或 m_ji = 0（至少有一个得是0）

📘例：
假设集合上关系 R 由下图矩阵表示，R 是自反的、对称的和反对称的吗？

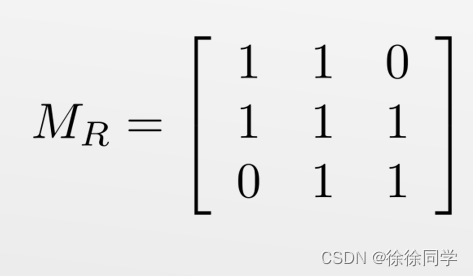
判断自反：因为这个矩阵中所有的对角线元素都等于1，所以 R 是自反的。
判断对称：由于 M_R 是对称的，所以 R 是对称的。
判断反对称：因为 m_1,2 和 m_2,1 都是1，所以 R 不是反对称的

⭐确定关系合成的矩阵

确定关系合成的矩阵：已知两个关系的关系矩阵，求这两个关系矩阵的合成矩阵

本质是关系矩阵的布尔积，理解上可以直接把两个矩阵相乘（注意顺序，A×B和B×A不一样），0仍是0，大于等于1的写成1

3、用有向图表示关系

有向图

定义： 一个有向图（directed graph,or digraph）由顶点（或结点）集 V 和边（或弧）集 E 组成，其中边集是 V 中元素的有序对的集合。顶点 a 叫作边 (a, b) 的始点，而顶点 b 叫作这条边的终点。

形如 (a, a) 的边用一条从顶点 a 到自身的弧表示，这种边叫作环（loop）

📘例1：
画出具有顶点 a、b、c 和 d；边 (a, b)、(a, d)、(b, b)、(b, d)、(c, a)、(c, b) 和 (d, b) 的有向图

📘例2：
有向图中所表示的关系 R 中的有序对是什么？

关系中的有序对 (x, y) 是：
R = { (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (3, 1), (3, 3), (4, 1), (4, 3) }

⭐从有向图中 确定关系具有的属性

自反性

图中的所有顶点必须都有环

对称性

如果 (x, y) 是一条边，那么 (y, x) 也是

反对称性

如果 (x, y) 为边（ x ≠ y ），则 (y, x) 不是边（ x ≠ y 时， (x, y) 和 (y, x) 最多出现一个）

按照反对称的原始定义说，如果(x, y) 为边且 (y, x) 为边，那么x = y

传递性

如果 (x, y) 和 (y, z) 是边，那么 (x, z) 也是边

📘例1：
从有向图中确定关系具有哪些属性 ？

自反的？不是，并非每个顶点都有一个环
对称的？是的，从一个顶点到另一个顶点没有边
反对称的？是的，从一个顶点到另一个顶点没有边
传递的？是的，因为从一个顶点到另一个顶点没有边

📘例2：
从有向图中确定关系具有哪些属性 ?

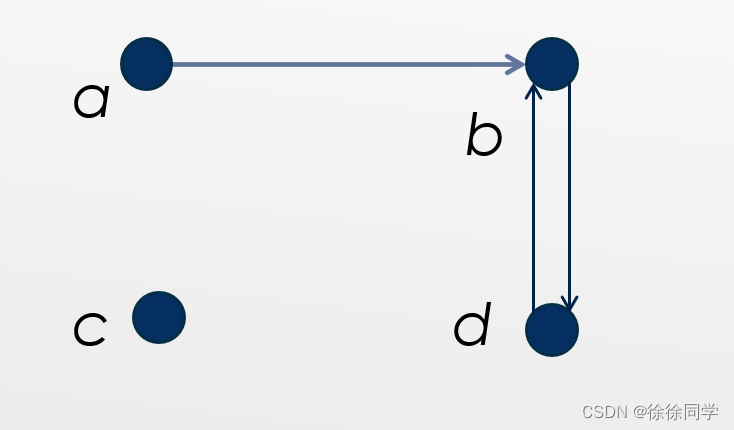
自反的？不是，一个环都莫得
对称的？不是，从 a 到 b 有一个边，但从 b 到 a 没有
反对称的？不是，从 d 到 b 以及从 b 到 d 有边
传递的？不是，从 a 到 c 以及从 c 到 b 有边，但是从 a 到 d 没有

📘例3：
从有向图中确定关系具有哪些属性 ？

自反的？不是，没有环
对称的？不是，比如从 c 到 a 就没有边
反对称的？是的，每当从一个顶点到另一个顶点存在边时，没有一个有 返回路径
传递的？不是，从 a 到 b 没有边

📘例4：
从有向图中确定关系具有哪些属性 ？

自反的？不是，没有环
对称的？不是，例如从 d 到 a 不存在边
反对称的？是的，无论哪条从一个顶点到另一个顶点的边，都没有返回路径
传递的？是的，没有第一个边结束于第二个边开始的顶点的两条边