机器学习 第二章 模型评估与选择【说人话版必能理解】

2.1 经验误差与过拟合

（1）精度与错误率

错误率=分错的样本/总样本

精度（“正确率”）=1-错误率

（2）训练误差/经验误差与泛化误差

训练误差：在训练集上产生的误差（做过的还错）

泛化误差：在新样本上产生的误差（我们期望很小的误差）

泛化误差越小学习器表现越好

（3）过拟合与欠拟合

过拟合：学习能力太强，把一些特征当成所有样本的特征

过拟合只能缓解，不能避免

欠拟合：学习能力太弱，没有学习到特征

2.2 评估方法——训练集测试集如何划分

我们要评估模型，也就是要求得泛化误差，所有我们通过在测试集上的误差来拟代表在所有未知严格样本上的泛化误差，那么我们本节的问题就是如何划分训练集和测试集

前提：训练集与测试集要尽可能保持数据分布的一致性（模拟考和高考都要覆盖所有知识点），至少保证样本的类别比例相似（好瓜：坏瓜=1：2）

（1）留出法

将D划分为两个互斥的集合，按照具体情况划分不同比例，多次划分得出平均结果

（2）交叉验证集（应用最广）

每一个数据都可能作为测试数据

k倍交叉验证：把D划分为k份，每次取一个数据集作为测试集，重复步骤直到其他份数据集也做训练，得到k个测试结果，取平均值。

p次k折交叉验证：上面的过程重复p次，共有p乘k个结果

留一法：数据集只有一种划分方式，所以每次只拿一个样本作为测试集

（3）自助法（数据量少的情况）

也称为有放回采样/可重复采样，在D中选一个样本拷贝到D',然再放回初始数据集D中

（4）调参与最终模型

在训练前我们要根据数据集对模型调整合适的参数，我们便在训练集中挑出来些数据作为”验证集“，调完后再放回训练集中训练。

2.3 性能度量

对模型泛化能力的评估，这些值就反应了这个模型好不好

（1）错误率和精度

（2）查准率、查全率与F1

查准率：挑出来的好瓜中有多少真的是好瓜——>不能挑错

查全率：真的是好瓜有多少被挑出来了——>不能挑不全

查准率（P）:P=所有认为的好瓜里真的是好瓜/所有认为的好瓜

查全率（R）:R=所有认为的好瓜里真的是好瓜/所有的好瓜

F1是查准率和查全率相等时的平衡点取值，它反应了查全率和查准率双高的条件下学习器的表现能力

F1=2X（两者之积/两者之和）

当多次训练有多个混淆矩阵时，有两种计算方式

宏：先算再平均

微：先平均再算

（3）ROC与AUC

在不同任务中，根据不同的任务需求截断点不同，截断点就是判断好瓜和坏瓜的分界线，例如：大于这个点就是好瓜，小于这个点就是坏瓜

ROC与AUC就是用于在不同情况的阈值条件下判断模型的表现的概念

ROC曲线：当改变阈值时，模型表现的是如何变化的，越靠左上角越好

AUC：模型的总体能力，越大越好

AUC=1，模型理想，全都能分对

AUC=0.5，跟随机猜测差不多

AUC=0，还不如瞎猜

（4）代价敏感错误率与代价曲线

把正例认成反例与把反例认成正例的代价是不一样的

虽然模型的错误率一致，但是由于错误情况付出的代价不同，所有我们把代价加入考虑，判断模型的好坏

取极值做归一化处理，表示出横轴和纵轴

取不同阈值条件下的情况绘制曲线得到

围成这个面积就是这个模型在不同条件下（不同阈值）的平均错误成本，面积越小整体代价越低，表现越好

2.4 比较检验——机器学习比较性能方法

由于上文说的三个原因

1.我们要比的是泛化性能，但是我们只能通过测试集上的性能近似得到泛化性能，两者之间不能完全等同

2.测试集上的性能与测试集本身选择有关

3.模型在同一参数多次运行时结果不同

所有我们不能直接比较我们第三节介绍的性能，那么我们本小节就学习机器学习比较性能的方法

（1）假设检验——单个模型单次/多次

比较两算法性能是否相同。

一般我们假设两算法性能一样，很显然，若拒绝，则性能不一样，若没拒绝则性能一样。

（2）交叉验证t检验——两个模型

用于比较两个模型的泛化误差。

• 通过 k 折交叉验证（如 10 折）获取多个评估分数。
• 计算两个模型的平均误差并进行 t 检验，判断它们是否有显著差异。

（3） McNemar 检验 ——两个模型

用于分类模型的错误模式比较。

• 统计两个模型在同一数据集上，正确/错误分类的情况。
• 如果两个模型的错误模式显著不同，则说明它们的性能存在差异。

（4）Friedman 检验 + Nemenyi 后续检验——多个模型

用于比较多个模型的表现。

• Friedman 检验：先判断多个模型的性能是否有整体差异。
• Nemenyi 后续检验（如果 Friedman 发现差异）：进一步分析具体哪些模型之间有显著区别。

2.5 偏差与方差——什么原因造成了泛化误差

上面的文字解释还是不太好理解，我类比一下实际应用的时候，一般我们数据集有三部分

image：原图（考题）

mask：人工分好的结果（考题正确的答案）

lable：模型预测出来的结果（模型写出来的答案）

方差【本次lable-平均lable】：有的考试发挥好，有的考试发挥不好，方差就是本次的考试发挥与平均考试发挥的差距

偏差【平均lable-mask】：平均考试发挥的差距（理想的发挥）与真正答案的差别

噪声【mask-lable】： 标注答案与真实世界之间的差异与不确定性，意思就是有些题目超纲了，我们找无数个学生也做不对，考题本身的问题

我们通过数学推理就能得出，我们最终的泛化误差就是方差+偏差+噪声

小声逼逼：启蒙一下，数学可以推到出一切，比如计算出几个看似完全不相干的东西之间的关系，“函数创造万物”，比如你今天穿的内裤颜色与食堂大爷穿的袜子颜色之间是有关系的，我们往往都是通过数学推导去证明他们之间的关系然后作为公理去进一步创造世界和改造世界，所以在学习的时候不必过度纠结和强求理解，毕竟我们也很难理解你今天穿的内裤颜色和食堂大爷穿的袜子颜色有什么关系，这就是数学的魅力虽然我也不喜欢哈哈）

所以这里我们就不纠结为什么方差+偏差+噪声真的就恰好等同于泛化误差了，再来个图理解一些

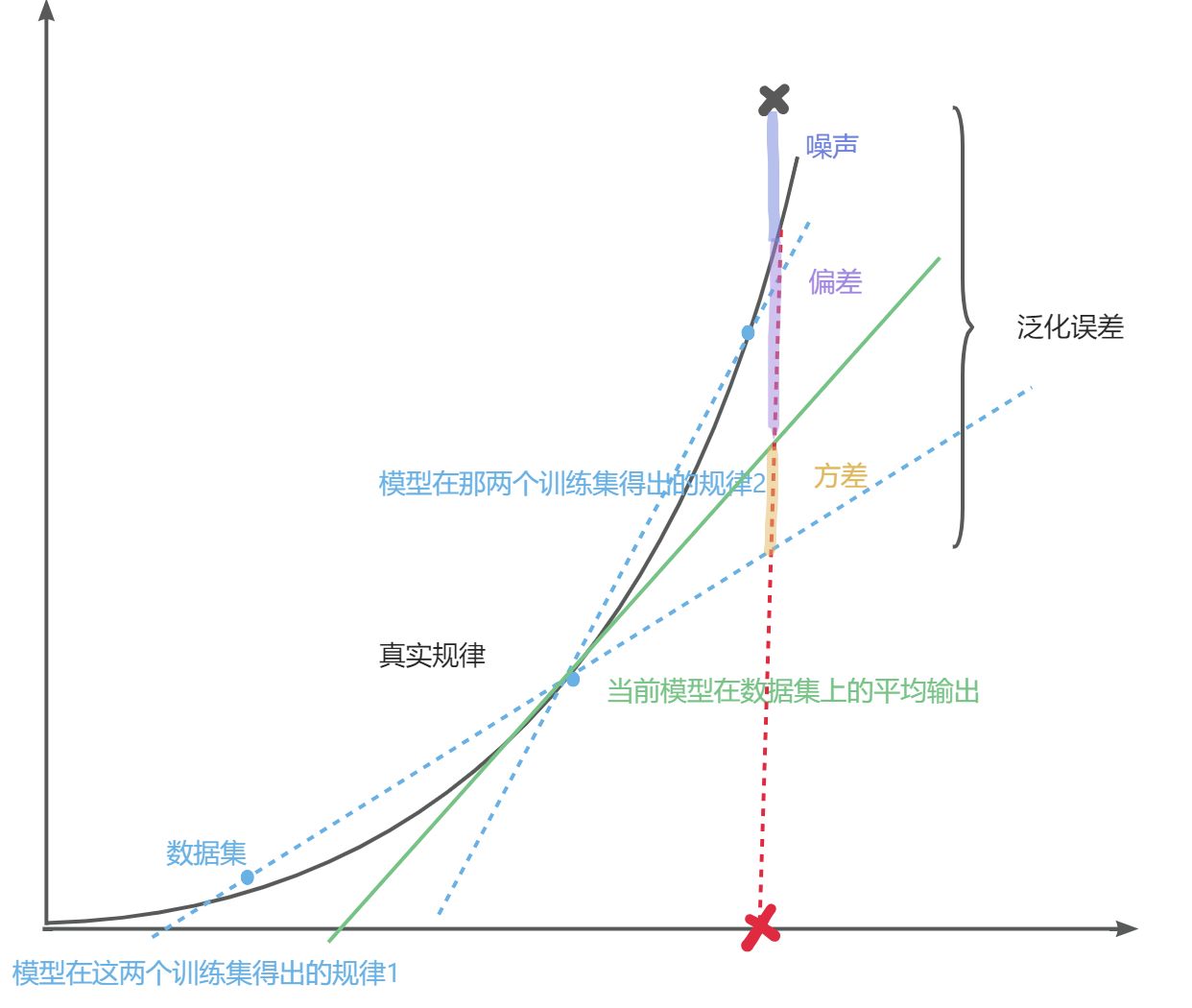
噪声无法避免，所以我们只有尽可能让方差和偏差减小，但是偏差和方差是有冲突的

模型简单，欠拟合时：偏差大，方差小——没学多少，每次模型都差不多

当拟合程度越来越深，学习能力越来越强

模型复杂，过拟合时：偏差小，方差大——跟真实值差不多，但是学习能力太强容易出洋相（把没有锯齿的树叶不当作树叶）