野人传教士过河问题

一、实验目的和要求

目的：使用状态空间表示法和状态转换图来解决过河问题

要求：输入：牧师人数（即野人人数）n，小船一次至多载客人数c。

输出：若问题无解，则显示“渡河失败”信息，否则，输出一组最佳方案，用三组（X1，X2，X3）表示渡河过程中的状态，并用箭头输出这些状态之间的迁移：目的状态<- <-中间状态 <- <-初始状态。

二、实验设备和实验环境

1、操作系统：Windows 10/11

2、代码运行环境：C++

三、实验任务

假如有n个牧师和n个野人准备渡河，但只有一条能容纳c个人的小船，为了防止野人侵犯牧师，要求无论在何处，牧师的人数不得少于野人的人数（除非牧师人数为0），且假定两种人都会划船。试设计一个算法，确定它们能否渡过河去，若能，则给出一只小船来回次数最少的最佳方案。调试、运行程序，观察、记录结果并分析。

四、实验预习过程

算法定义：

状态空间：一个问题的全部状态及一切可用算符构成的集合。

常用一个三元组表示为：(S, F, G)，其中，S为问题的所有初始状态集合；F为算符的集合；G为目标状态的集合。

状态空间也可用一个有向图来表示，该有向图称为状态空间图。在状态空间图中，节点表示问题的状态，有向边表示算符。

请画出本实验的程序流程图。

//传教士和野人数量都为三，船每次最多运送2人情况下，算法流程图

五、具体代码

#include <iostream>
#include <queue>
#include <set>
#include <tuple>

using namespace std;

// 定义状态的结构体
struct State {
    int missionariesLeft;
    int cannibalsLeft;
    int missionariesRight;
    int cannibalsRight;
    bool boatOnLeft;

    // 状态的构造函数
    State(int mL, int cL, int mR, int cR, bool bOL)
        : missionariesLeft(mL), cannibalsLeft(cL), missionariesRight(mR), cannibalsRight(cR), boatOnLeft(bOL) {}

    // 重载比较运算符，用于状态的集合
    bool operator<(const State& other) const {
        return tie(missionariesLeft, cannibalsLeft, missionariesRight, cannibalsRight, boatOnLeft) <
            tie(other.missionariesLeft, other.cannibalsLeft, other.missionariesRight, other.cannibalsRight, other.boatOnLeft);
    }
};

// 检查状态是否有效
bool isValidState(const State& state) {
    int mL = state.missionariesLeft;
    int cL = state.cannibalsLeft;
    int mR = state.missionariesRight;
    int cR = state.cannibalsRight;

    // 如果食人魔的数量大于传教士，则不合法
    if (cL > mL && mL > 0 || cL < 0) return false;
    if (cR > mR && mR > 0 || cL < 0) return false;
    return true;
}

// BFS搜索解法
void solveProblem() {
    queue<pair<State, vector<State>>> bfsQueue;
    set<State> visitedStates;
    int N, K;
    cout << "请输入分别传教士和野人的数量： ";

    cin >> N >> K;
    State initialState(N, K, 0, 0, true);
    cout << endl << "请输入每条船最多乘坐人数：  ";
    int i = 0;
    cin >> i;
    // 初始状态
    //State initialState(3, 3, 0, 0, true);
    bfsQueue.push(make_pair(initialState, vector<State>{initialState}));
    visitedStates.insert(initialState);

    while (!bfsQueue.empty()) {
        State currentState = bfsQueue.front().first;
        vector<State> currentPath = bfsQueue.front().second;
        bfsQueue.pop();

        // 检查是否达到目标状态
        if (currentState.missionariesLeft == 0 && currentState.cannibalsLeft == 0) {
            cout << "找到解决方案如下：" << endl;
            cout << "(左岸传教士，左岸野人，右岸传教士，右岸野人，船的位置)" << endl;
            for (const State& state : currentPath) {
                cout << "(" << state.missionariesLeft << ", " << state.cannibalsLeft << ", "
                    << state.missionariesRight << ", " << state.cannibalsRight << ", "
                    << (state.boatOnLeft ? "左岸" : "右岸") << ")" << endl;
            }
            return;
        }

        // 生成下一个可能的状态

        for (int m = 0; m <= i; ++m) {
            for (int c = 0; c <= i; ++c) {
                if (m + c == 0 || m + c > i) continue;  // 至少一个人划船，最多两个人

                // 计算新状态
                State newState = currentState;
                newState.boatOnLeft = !currentState.boatOnLeft;
                if (currentState.boatOnLeft) {
                    newState.missionariesLeft -= m;
                    newState.cannibalsLeft -= c;
                    newState.missionariesRight += m;
                    newState.cannibalsRight += c;
                }
                else {
                    newState.missionariesLeft += m;
                    newState.cannibalsLeft += c;
                    newState.missionariesRight -= m;
                    newState.cannibalsRight -= c;
                }

                // 检查新状态是否有效且未被访问过
                if (isValidState(newState) && visitedStates.find(newState) == visitedStates.end()) {
                    visitedStates.insert(newState);
                    vector<State> newPath = currentPath;
                    newPath.push_back(newState);
                    bfsQueue.push(make_pair(newState, newPath));
                }
            }
        }
    }

    cout << "没有找到解决方案." << endl;
}

int main() {
    solveProblem();
    return 0;
}

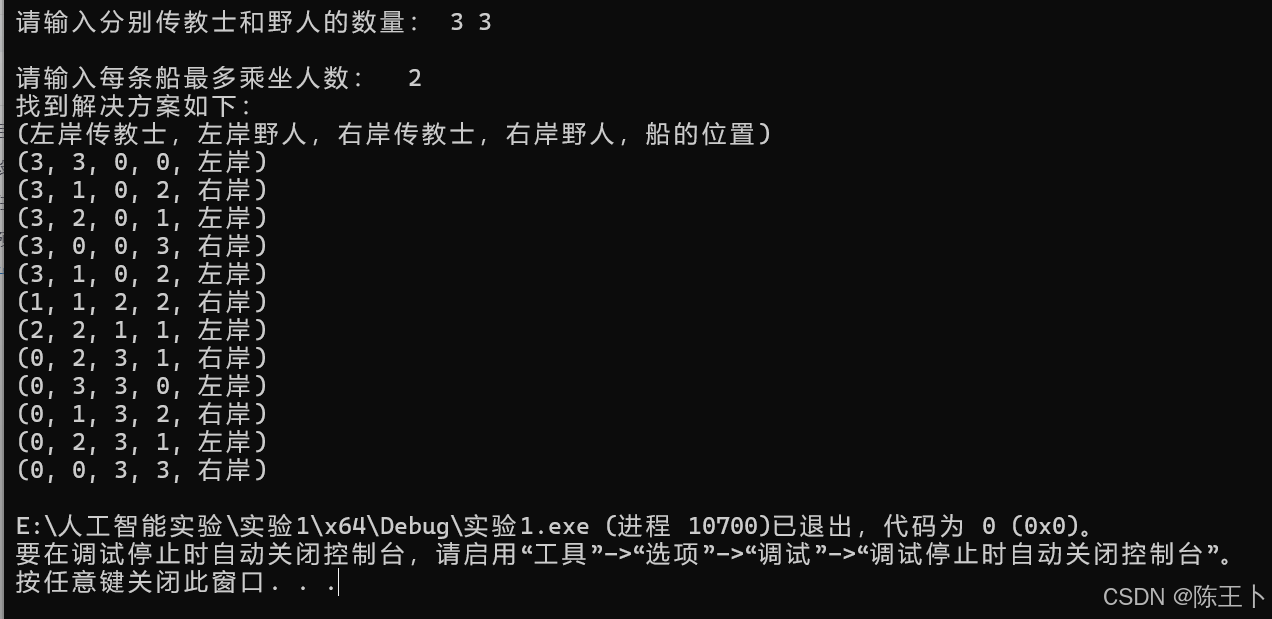
六、效果展示