[数值计算方法] 零基础的学习资料和总结 （ c语言描述版本）

本系列内容主要针对数值计算方法

第一部分 引言（误差、有效数字、减小误差的方法）

第二部分 非线性方程解法（二分法、牛顿迭代法等）

第三部分 线性方程解法（直接法和迭代法）

第四部分 差值与曲线拟合（拉格朗日、牛顿插值法、最小二乘法等）

第五部分 数值积分与数值微分（牛顿-柯特斯公式，复化积分法等）

第六部分 常微分方程的初值问题的解法

---

引言入门

目录

前言

一、为什么要学习《数值计算方法》

二、数值计算引论

1.误差

误差的来源

误差的表示

2.有效数字

3.减小误差的方法

总结

---

前言

        本系列内容主要是以《数值计算方法》——马东升、董宁 第三版为主，个人心得和见解为辅的内容分享。计划涵盖的内容包括但不限于算法实现与优化、实际应用案例等。通过这些内容，我希望能够为大家提供一些有价值的思考和启发，帮助大家更好地理解和运用数值计算方法解决实际问题，废话不多说，直接进入正题。
 

---

一、为什么要学习《数值计算方法》

        这个问题是要我们自己思考的，为什么要学一门课是对自己未来的规划，这个小部分只是为了我的排版美观，但是这个问题是值得大家深思的。而我对这门课的理解如下：

简单地说，就是研究如何用计算机有效地解决一个数学问题。具体的操作流程图如下

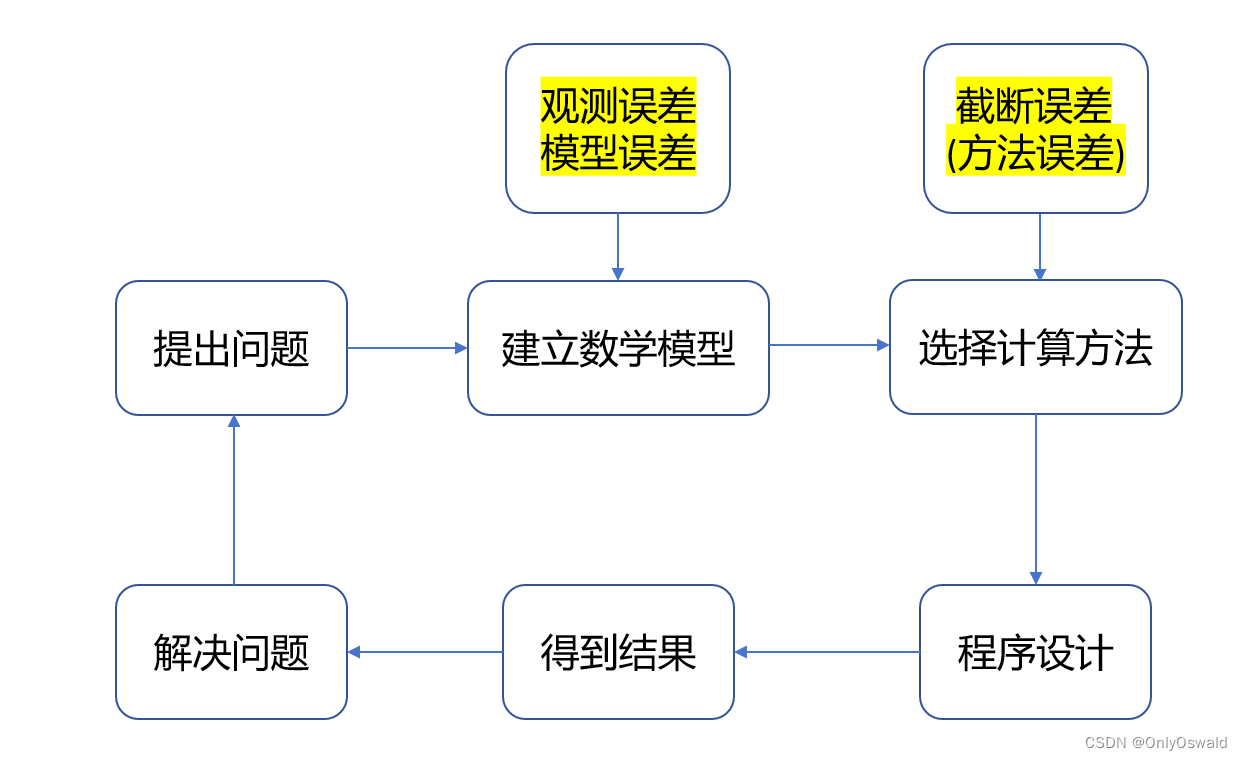
二、数值计算引论

1.误差

误差的来源

        误差是怎么产生的呢？

        模型误差：模型误差是指选择的数学模型与实际问题的真实情况之间的差异。

• 例子： 如果我们用线性模型 𝑔(𝑥)=2𝑥 来逼近非线性函数 𝑓(𝑥)=𝑥^2                                                          那么模型误差就是 𝑓(𝑥)−𝑔(𝑥)=𝑥^2−2𝑥。

        观测误差：观测误差是由于测量设备的限制或不准确性导致的测量值与真实值之间的差异。

• 例子：我们测量一个物体长度为 10 厘米，但实际上它的长度是 10.2 厘米，那么其观测误差就是∣10.2−10∣=0.2厘米。

        截断误差：当有限过程代替无限过程的误差（无穷级数求和，只能取前面有限项求和来近似代替）。这种计算方法本身出现的误差，所以也称为方法误差。

• 例子： 对于指数函数 𝑒^𝑥，其泰勒级数展开为：  其中Truncation Error就是截断误差

        舍入误差：其产生原因一般是计算机字长有限，一般实数不能精确存储，于是产生舍入误差。

• 例子： 考虑在计算机中对浮点数的加法运算。运行下面代码（c语言）你会发现在运行后会出现这样神奇的结果“0.1 + 0.2 = 0.3000000119”，这是因为计算机字长有限，一般实数不能精确存储。

#include <stdio.h>

int main() {
    float a = 0.1;
    float b = 0.2;
    float result = a + b;

    printf("0.1 + 0.2 = %.10f\n", result);

    return 0;
}

---

 讲完上面误差的来源接下来就是误差的表示

误差的表示

误差的表示有四个关键词：绝对误差e*、相对误差er*、绝对误差限ɛ*、相对误差限ɛr*

其中 真实值S是真实值，一般有特定的指派或者题目给出，对于上面四个参数有下面关系公式

而对于 相对误差限 绝对误差限 n值 是三者知一可得其他二值的，具体公式如下。

其中n就涉及到下一部分'有效数字'
        

2.有效数字

         其中 n为'n位有效数字' 通常包括从该数值最左边的非零数字开始，一直到最右边的数字（包括末尾的零）的位数，有两点需要注意：

        有效数字位数相同的两个近似数，绝对误差不一定相同。

        有效数字位与小数点后有多少位数无直接关系。

        例如：123.45是五位有效数字  0.0001是一位有效数字 1.23*10^3=1230是四位有效数字

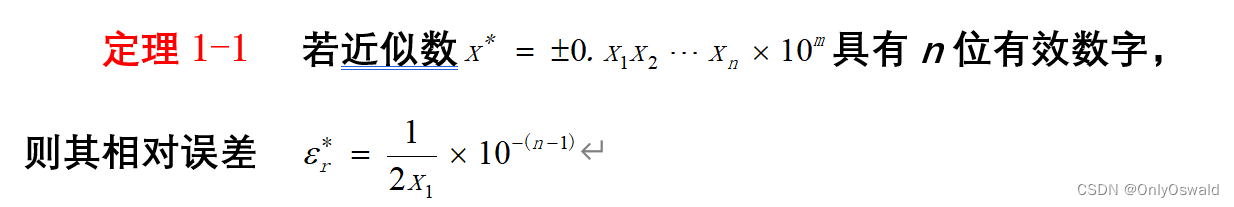
       其中X1表示第一位有效数字的值，例如2.3413的X1就是2。

        对于这一定理，其中的条件只是一个充分条件而非必要条件。近似的有效数字位数越多其相对误差一定越小。但是，相对误差越小，有效数字的位数不一定多。

        对于这一部分我运用《数值计算方法》——马东升、董宁 第三版第10页内容展开讲解（如有侵权，联系我删除）

        对于此题：
        1.找出X1=2；

        2.利用定理一算出-（n-1）从而得到n

        3.确定有效位数，计算题目要求的值

• 此定理给出的是一个充分条件，而不是必要条件。所以定理的逆命题不成立。即若近似数有n位有效数字，相对误差不一定满足定理。
• 在实际应用时，为了要使所取近似数具有n位有效数字，要求所取近似数的相对误差满足定理1-2的要求。

3.减小误差的方法

• 避免两相近数相减

        避免10.002-10.001这样的计算式

• 防止“大数”吃掉“小数”

        一般不建议数量级相差10^8次方及以上的数进行加减法，例如0.12*10^5+0.7*10^-3这种计算，计算机可能会略去0.7*10^-3部分，因此可能需要修改程序，造成不必要的麻烦。

• 绝对值太小的值不宜为除数

        即0.000001这类的小数不适合当除数，这样会导致计算中出现极大数，我在处理文件时出现过“几万”的数字变成“3E18”这种数字，其原因可能就是小数在某一部充当的除数，导致你的数字越出了“界限”（例如int的范围是-32768～32767），当你超出这个范围就会出现计算错误。

• 简化计算步骤，减少运算次数

        对于这一步，我开头有提过0.1 + 0.2 = 0.3000000119，这种情况，每次计算都可能出现这种小误差，但是计算步骤多了，误差也会随之增多。

---

总结

        这是我的第一篇博客，可能会出现小问题和错误，欢迎大家批评指正，希望我的内容可以给学习《数值计算方法》的大家带来帮助。