滑动窗口算法详解：从理论到实战（LeetCode 3 & 438）

最新推荐文章于 2025-05-20 19:46:55 发布

一个Potato

最新推荐文章于 2025-05-20 19:46:55 发布

阅读量812

点赞数 9

文章标签：算法 leetcode

本文链接：https://blog.csdn.net/m0_74655006/article/details/148066925

版权

一、算法思想

滑动窗口是一种处理数组/字符串子区间问题的高效算法，通过维护一个动态变化的窗口区间，用双指针（左指针left、右指针right）在O(n)时间复杂度内解决问题。

核心特点：

窗口动态调整：右指针探索新元素，左指针收缩无效区间
状态实时更新：用哈希表等数据结构记录窗口内元素状态
避免重复计算：通过指针移动而非重新遍历来更新结果

二、典型案例分析

案例1：无重复字符的最长子串（LeetCode 3）

3. 无重复字符的最长子串 - 力扣（LeetCode）

题目描述

找出字符串中不包含重复字符的最长子串长度

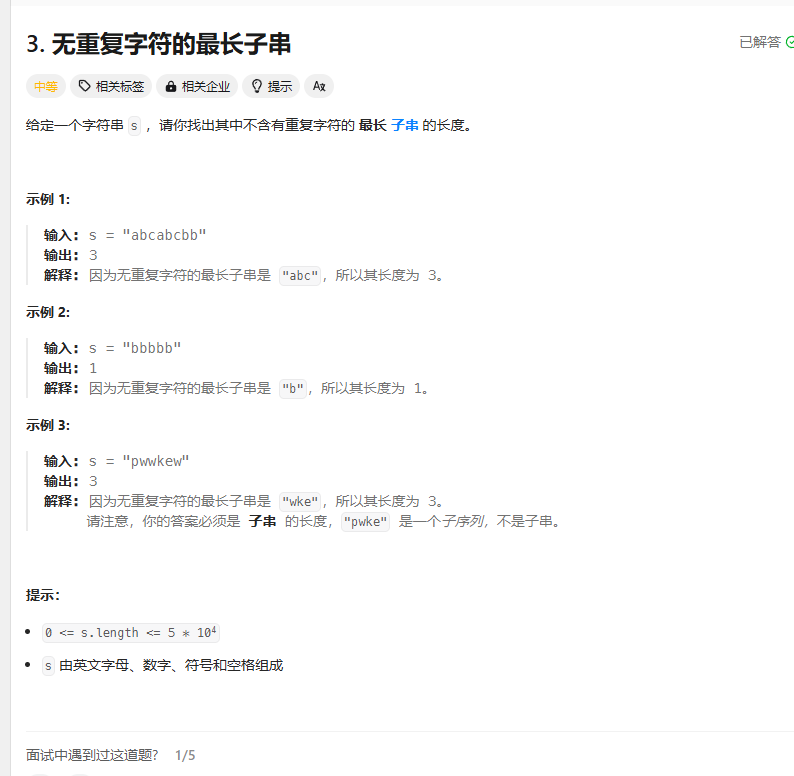
算法思路：

我们先从每一个题目给出的字符开始，找出不同的不重复的最长子串，我们可以发现，当我们增加子串的起始位置时，终点位置也是一样增加的，所以我们设置滑动窗口的时候，只需要遍历所有的左指针，然后我们

class Solution {
public:
    // 查找连续且不重复的子串   
    int lengthOfLongestSubstring(string s) {
        // 用哈希表记录每一个字符出现的次数
        unordered_set<char> occ;
        // 初始化右指针为-1，表示一开始这个指针在左指针的左边
        int right = -1, ans = 0;
        int n = s.size();
        // 开始遍历所有的左指针
        for(int i = 0; i < n; i++){
            if(i != 0){
                // 如果不是初始的状态的话，就要减去之前子串的第一个字符
                occ.erase(s[i - 1]);
            }
            while(right + 1 < n && !occ.count(s[right + 1])){
                // 如果说右边界+1没有越界，并且这个字符之前没有出现过的话，就可以添加
                occ.insert(s[right + 1]);
                right++;
            }
            ans = max(ans, right - i + 1);
        }
        return ans;
    }
};

关键点分析

哈希表记录位置：快速判断重复并定位
左指针跳跃：遇到重复时直接跳到重复字符的下一位
ABBA情况处理：max()保证指针不反向移动

复杂度

时间复杂度：O(n)
空间复杂度：O(字符集大小)

案例2：找到字符串中所有字母异位词（LeetCode 438）

438. 找到字符串中所有字母异位词 - 力扣（LeetCode）

题目描述

给定字符串s和p，找到s中所有p的字母异位词的子串起始索引

算法思路：

首先，根据题目我们得知，s的字符串的长度必须要大于等于p的字符串的长度，不然的话，是不可能获得关于p的异位词的。

// 如果说s的长度比p的长度要小的话，证明字符串s中一定不存在字符串p的异位词。
if(sLen < pLen){
     return vector<int>();
}

然后，我们需要获得每一个滑动窗口中，每一个字符的出现次数，滑动窗口的大小保持不变（根据题目要求可得），在算法的实现中，我们可以使用数组来存储字符串 p 和滑动窗口中每种字母的数量。

// 如果从0开始到pLen-1的子串符合题目要求，增加0索引到结果的集合中
if (sCount == pCount) {
	ans.emplace_back(0);
}
// 在s中构造一个长度为与字符串p的长度相同的滑动窗口，并在滑动中维护窗口中每种子符的数量
for (int i = 0; i < sLen - pLen; i++) {
	--sCount[s[i] - 'a'];       // 这个表示移除左边界字符
	++sCount[s[i + pLen] - 'a'];
	if (sCount == pCount) {
		ans.emplace_back(i + 1);        // 添加索引到结果中
	}
}

最终算法实现

class Solution {
public:
    vector<int> findAnagrams(string s, string p) {
        int sLen = s.size(), pLen = p.size();   // 获得s和p的字符串长度
        // 如果说s的长度比p的长度要小的话，证明字符串s中一定不存在字符串p的异位词。
        if(sLen < pLen){
            return vector<int>();
        }
        vector<int> ans;        // 保存有多少个结果
        vector<int> sCount(26); // s字符串有多少个字母出现
        vector<int> pCount(26); // p字符串有多少个字母出现
        for(int i = 0; i < pLen; i++){
            ++sCount[s[i] - 'a'];       // 开始统计每一个数字的大小
            ++pCount[p[i] - 'a'];
        }

        if(sCount == pCount){
            ans.emplace_back(0);
        }
        // 在s中构造一个长度为与字符串p的长度相同的滑动窗口，并在滑动中维护窗口中每种子符的数量
        for(int i = 0; i < sLen - pLen; i++){
            --sCount[s[i] - 'a'];       // 这个表示移除左边界字符
            ++sCount[s[i + pLen] - 'a'];
            if(sCount == pCount){
                ans.emplace_back(i + 1);        // 添加索引到结果中
            }
        }

        return ans;
    }
};

关键点对比

特性	案例1	案例2
窗口类型	可变长度	固定长度
核心数据结构	哈希表记录位置	频率数组/哈希表
指针移动策略	跳跃式移动	滑动式移动
结果更新时机	每次移动右指针时	窗口达到大小时

三、滑动窗口通用模板

#include <unordered_map>
#include <string>

using namespace std;

int sliding_window_template(const string& s) {
    int left = 0;                     // 左指针初始化
    unordered_map<char, int> counter; // 滑动窗口计数器
    int result = 0;                   // 最终结果存储
    
    for (int right = 0; right < s.size(); ++right) {
        // 1. 将s[right]加入窗口（示例：字符计数）
        char c = s[right];
        counter[c]++;
        
        // 2. 判断收缩窗口的条件（根据具体问题实现）
        while (/* 窗口需要收缩的条件，例如：counter[c] > 1 */) {
            // 3. 可选：记录/更新中间结果
            // result = max(result, right - left);
            
            // 4. 移出左边界元素
            char left_char = s[left];
            if (--counter[left_char] == 0) {
                counter.erase(left_char); // 清除空计数
            }
            left++; // 收缩窗口
        }
        
        // 5. 更新最终结果（根据问题需求调整位置）
        result = max(result, right - left + 1);
    }
    
    return result;
}