【数据结构】实验一

题

题目：
实现以下内容：
1.从终端输入两个数列，分别存储在两个链表A和B中，并将两个链表的内容交替合并，合并成一个新的链表C，输出ABC三个链表。
2.对链表C，删除重复元素得到链表D并输出，对于链表中的重复元素要求保留第一次出现的元素。
3.输入一个整数k，将链表D按从左至右的顺序分成多个长度为k的区间，对于每个区间：
3.1 如果区间内节点数等于k则将该区间节点顺序反转
3.2 如果最后一个区间节点数小于k则保持原有顺序
按照上述要求输出结果链表E。
要求：
1.给出算法设计思想并用C++实现。
2.分析算法的时间复杂度和空间复杂度。

输入样例
输入：
A：2 4 8 1 5
B：H 5 C D E 4 F G
k：3
输出：
2 4 8 1 5
H 5 C D E 4 F G
2 H 4 5 8 C 1 D 5 E 4 F G
2 H 4 5 8 C 1 D E F G
4 H 2 C 8 5 E D 1 F G

一种答案

完整代码：

#include <iostream>
#include <vector>
#include <sstream>
#include <unordered_set>
using namespace std;

// 定义链表节点
struct ListNode 
{
    char value;
    ListNode* next;

    // 构造函数
    ListNode(char x) : value(x), next(nullptr) {}
};

// 创建链表
ListNode* createLinkedList(const vector<char>& values) 
{
    
    //如果 values 向量为空（即没有元素），则直接返回 nullptr，表示创建了一个空链表。
    if (values.empty()) return nullptr;

    // 使用 new 关键字动态分配内存，创建一个新的 ListNode 对象，其值为 values[0]（向量的第一个元素）。
    // head 指针指向这个新创建的节点，作为链表的头节点。
    ListNode* head = new ListNode(values[0]);

    ListNode* current = head;

    // size_t 是一种无符号整数类型(不会出现负数)
    for (size_t i = 1; i < values.size(); ++i) 
    {
        current->next = new ListNode(values[i]);
        current = current->next;
    }
    return head;
}

// 打印链表
void printLinkedList(ListNode* head) {
    while (head) {
        cout << head->value << " -> ";
        head = head->next;
    }
    cout << "nullptr" << std::endl;
}


// 交替合并两个链表
ListNode* alternateMerge(ListNode* list1, ListNode* list2) 
{
    ListNode dummy(0); // 使用哑节点简化边界条件
    ListNode* tail = &dummy;

    while (list1 && list2) 
    {
        tail->next = list1;
        list1 = list1->next;
        tail = tail->next;

        tail->next = list2;
        list2 = list2->next;
        tail = tail->next;
    }

    // 如果有剩余的元素
    tail->next = list1 ? list1 : list2;

    return dummy.next;
}


// 删除链表中的重复元素
ListNode* removeDuplicates(ListNode* head) {
    if (!head) return nullptr;

    unordered_set<char> seen; // 用于存储已经出现过的元素
    ListNode* current = head;
    ListNode* prev = nullptr;

    while (current) {
        if (seen.find(current->value) != seen.end()) {
            // 当前节点的值已经在 set 中，删除当前节点
            prev->next = current->next;
            delete current;
            current = prev->next;
        }
        else {
            // 当前节点的值不在 set 中，添加到 set 并继续
            seen.insert(current->value);
            prev = current;
            current = current->next;
        }
    }

    return head;
}


// 反转链表区间
ListNode* reverseKGroup(ListNode* head, int k) {
    if (!head || k <= 1) return head;

    // 哑节点用于简化边界条件
    ListNode dummy(0);
    dummy.next = head;
    ListNode* prev = &dummy;
    ListNode* end = head;

    while (true) {
        // 查找当前区间的结束节点
        for (int i = 0; i < k && end; ++i) {
            end = end->next;
        }

        // 如果当前区间不足 k 个节点，则直接返回
        if (!end) break;

        // 断开当前区间与后续节点的连接
        ListNode* start = prev->next;
        ListNode* nextPrev = start;
        ListNode* current = start->next;
        start->next = end;

        // 反转当前区间
        while (current != end) {
            ListNode* next = current->next;
            current->next = start;
            start = current;
            current = next;
        }

        // 连接前一个区间和反转后的区间
        prev->next = start;
        prev = nextPrev;

        // 移动到下一个区间
        end = prev->next;
    }

    return dummy.next;
}



// 释放链表内存
void freeLinkedList(ListNode* head) {
    while (head) {
        ListNode* temp = head;
        head = head->next;
        delete temp;
    }
}



int main() 
{
    string input_a, input_b;
    vector<char> list_a, list_b;

    // 输入第一个数列
    cout << "请输入第一个数列（以空格分隔）: ";
    getline(cin, input_a);
    stringstream ss(input_a);
    char num;
    while (ss >> num) 
    {
        list_a.push_back(num);
    }

    // 输入第二个数列
    cout << "请输入第二个数列（以空格分隔）: ";
    getline(cin, input_b);
    stringstream ss2(input_b);
    while (ss2 >> num) 
    {
        list_b.push_back(num);
    }

    // k
    int k;
    cout << "请输入一个整数k（区间长度）: ";
    cin >> k;
    // 链表A
    ListNode* linked_list_a = createLinkedList(list_a);
    // 打印链表A
    cout << "链表A: ";
    printLinkedList(linked_list_a);
    
    // 链表B
    ListNode* linked_list_b = createLinkedList(list_b);
    // 打印链表B
    cout << "链表B: ";
    printLinkedList(linked_list_b);
    
    // 交替合并链表
    ListNode* merged_list_c = alternateMerge(linked_list_a, linked_list_b);
    // 打印链表C
    cout << "链表C: ";
    printLinkedList(merged_list_c);

    // 链表D
    ListNode* list_d = removeDuplicates(merged_list_c);
    // 打印链表D
    cout << "链表D: ";
    printLinkedList(list_d);

    // 链表E
    ListNode* list_e = reverseKGroup(list_d,k);
    // 打印链表E
    cout << "链表E: ";
    printLinkedList(list_e);

    // 清理内存
    freeLinkedList(merged_list_c);

    return 0;
}

头文件

先介绍几个头文件。

1.vector

参考: C++详解vector
在C++编程中，vector 是标准模板库（Standard Template Library, STL）提供的一个容器类。它是一个能够存储任意类型元素的动态数组，提供了许多有用的功能来处理和操作这些元素。与传统的数组不同，vector 可以根据需要自动调整其大小，并且可以方便地添加或删除元素。（动态数组，无需自己手动开空间和放空间。）

包含头文件

#include<vector>

声明一个 vector 来存储特定类型的数据，例如整数、浮点数或者自定义的对象等。

vector<int> myVector1;	// 创建一个空的 vector 用于存储 int 类型的数据
vector<int> myVector2 = {1, 2, 3, 4, 5};	// 使用初始化列表创建 vector

常用成员函数

push_back(value): 在向量末尾添加一个元素。
pop_back(): 移除向量末尾的元素。
size(): 返回向量中元素的数量。
empty(): 如果向量为空则返回 true。
clear(): 清空向量中的所有元素。
at(index): 访问指定索引位置的元素，如果索引越界会抛出异常。
front(): 返回第一个元素的引用。
back(): 返回最后一个元素的引用。
begin(): 返回指向第一个元素的迭代器。
end(): 返回指向最后一个元素之后位置的迭代器。
insert(position, value): 在指定的位置插入一个元素。
erase(position): 移除指定位置的元素。

迭代器

vector 支持迭代器，可以用来遍历 vector 中的所有元素。

for (auto it = myVector.begin(); it != myVector.end(); ++it) 
{
    std::cout << *it << " ";
}
// 或者使用范围 for 循环
for (int &value : myVector) 
{
    std::cout << value << " ";
}

内存管理

vector 会在需要时自动重新分配内存来适应新的容量需求。如果你预先知道将要存储的元素数量，可以通过 reserve() 函数预留空间以避免不必要的重新分配。

myVector.reserve(100);	// 预留空间至少能容纳 100 个元素

小结

vector 是非常强大且灵活的容器，在C++编程中被广泛使用。
本题中的应用：

   vector<char> list_a,list_b;
...
   /*
   // 输出 list_a
   cout << "列表A的内容: ";
   for (const auto& value : list_a) 
   {
       cout << value << " ";
   }
   cout << endl;

   // 输出 list_b
   cout << "列表B的内容: ";
   for (const auto& value : list_b) 
   {
       cout << value << " ";
   }
   cout << endl;
   */
   //const：表示 value 是常量引用，这意味着在循环体内你不能修改 value 的值。
   //auto：是一个类型推导关键字，编译器会自动推断 value 的类型。在这个例子中，value 的类型将与 list_a 中元素的类型相同。
   //&：表示 value 是对容器中元素的引用。使用引用可以避免复制元素，提高性能。
   //value：是当前迭代的元素的名称。

这里复习一下C++中引用（主要是我忘记了lol）。
在 C++ 中，引用（reference）是一种特殊的变量类型，它提供了对另一个变量的别名。引用必须在声明时初始化，并且一旦初始化后就不能再指向其他对象。引用的主要用途是提供一种更方便的方式来操作复杂的对象，同时避免复制这些对象。

引用基本用法

type& ref = variable
//type 是引用所引用的变量的类型。
//& 表示这是一个引用。
//ref 是引用的名称。
//variable 是被引用的变量

引用的特点
别名：
引用是现有变量的别名，而不是一个新的独立变量。
对引用的操作实际上是对被引用变量的操作。
初始化：
引用必须在声明时初始化，不能先声明后初始化。
初始化后，引用不能再指向其他变量。
无空引用：
引用总是引用某个有效的对象，不能像指针那样为 nullptr。
常量引用：
可以使用 const 修饰符来创建常量引用，使得通过引用不能修改被引用的对象。

基本引用：

#include <iostream>
using namespace std;

int main() {
    int x = 10; // 定义一个整数变量
    int& ref = x; // 定义一个引用，引用 x

    cout << "x: " << x << endl; // 输出 x 的值
    cout << "ref: " << ref << endl; // 输出 ref 的值

    ref = 20; // 修改 ref 的值，实际上是修改 x 的值
    cout << "x after modification: " << x << endl; // 输出修改后的 x 的值
    cout << "ref after modification: " << ref << endl; // 输出修改后的 ref 的值

    return 0;
}

输出
x: 10
ref: 10
x after modification: 20
ref after modification: 20

常量引用：

#include <iostream>
using namespace std;

int main() {
    int x = 10;
    const int& cref = x; // 定义一个常量引用，引用 x

    cout << "x: " << x << endl;
    cout << "cref: " << cref << endl;

    // cref = 20; // 错误：不能通过常量引用修改 x 的值

    x = 20; // 仍然可以通过原始变量修改 x 的值
    cout << "x after modification: " << x << endl;
    cout << "cref after modification: " << cref << endl;

    return 0;
}

输出
x: 10
cref: 10
x after modification: 20
cref after modification: 20

2.sstream

本题中的应用：

	string input_a, input_b;

    // 输入第一个数列
    cout << "请输入第一个数列（以空格分隔）: ";
    
    getline(cin, input_a);
    //getline(cin, input_a)是 C++ 中用来从标准输入（通常是键盘）读取一行文本的函数。
    //这个函数会读取用户输入直到遇到换行符（即用户按下 Enter 键），
    //并将读取的内容存储到 input_a 字符串中。
    //换行符本身不会被包含在 input_a 中。
    
    stringstream ss(input_a);
    //stringstream ss(input_a) 这一行代码创建了一个 stringstream 对象，
    //并初始化 input_a 。
    //这样，你就可以使用流操作（如 >> 和 <<）来处理 input_a 中的数据了。

    char num;	//用来存储解析出的字符
    while (ss >> num) 	//从 stringstream 中读取下一个字符
    {
        list_a.push_back(num);	//将读取到的字符添加到 vector 中
    }

3.unordered_set

#include <unordered_set> 是C++标准库中的一个头文件，它提供了 std::unordered_set 容器的定义。std::unordered_set 是一种关联容器，它包含唯一对象的集合，这些对象通常是无序存储的，但它们是基于哈希表实现的，因此在平均情况下可以提供常数时间复杂度的查找、插入和删除操作。

创建和初始化

unordered_set< int > mySet

unordered_set< std::string > names = {“Alice”, “Bob”, “Charlie”}

#include <iostream>
#include <unordered_set>
#include <string>

int main() {
    // 创建一个空的 unordered_set
    std::unordered_set<int> mySet;

    // 使用初始值列表初始化
    std::unordered_set<std::string> names = {"Alice", "Bob", "Charlie"};

    return 0;
}

插入元素

mySet.insert(10);
mySet.insert(20);
mySet.insert(30);

// 或者使用 emplace 来直接构造元素（可能更高效）
mySet.emplace(40);

访问元素

std::unordered_set 不支持通过索引或键来直接访问元素，因为它是无序的。但是你可以检查某个元素是否存在：

if (mySet.find(20) != mySet.end()) {
    std::cout << "20 is in the set." << std::endl;
} else {
    std::cout << "20 is not in the set." << std::endl;
}

删除元素

mySet.erase(20);  // 删除值为 20 的元素

遍历迭代

for (const auto& elem : mySet) {
    std::cout << elem << " ";
}
std::cout << std::endl;

大小和容量

std::cout << "Size: " << mySet.size() << std::endl;
std::cout << "Bucket count: " << mySet.bucket_count() << std::endl;

分析链表

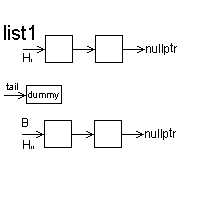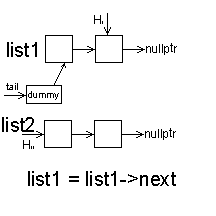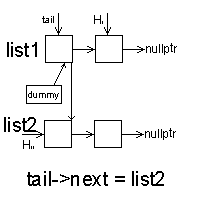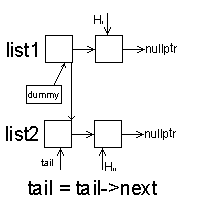
1.交替合并两个链表

// 交替合并两个链表
ListNode* alternateMerge(ListNode* list1, ListNode* list2) 
{
    ListNode dummy(0); // 使用哑节点简化边界条件
    ListNode* tail = &dummy;

    while (list1 && list2) 
    {
        tail->next = list1;
        list1 = list1->next;
        tail = tail->next;

        tail->next = list2;
        list2 = list2->next;
        tail = tail->next;
    }

    // 如果有剩余的元素
    tail->next = list1 ? list1 : list2;

    return dummy.next;
}

时间复杂度

• 遍历链表：在 while (list1 && list2) 循环中，我们每次迭代都会从 list1 和 list2 各取一个节点。因此，这个循环最多会执行 min(m, n) 次，其中 m 是 list1 的长度，n 是 list2 的长度。
• 处理剩余节点：在 while 循环之后，如果其中一个链表还有剩余的节点，我们会直接将这些剩余的节点链接到新链表的末尾。这部分操作最多需要 max(m, n) - min(m, n) 次。

综合以上两部分，整个函数的时间复杂度是 O(m + n)，即线性时间复杂度，因为每个节点只被访问一次。

空间复杂度

• 哑节点：我们创建了一个哑节点 dummy 用于简化边界条件。这个哑节点只占用常数级别的额外空间。
• 指针变量：我们使用了一些额外的指针变量（如 tail），这些变量也只占用常数级别的额外空间。
• 不创建新的节点：在这个函数中，我们并没有创建任何新的节点，只是重新排列了现有的节点。

因此，该函数的空间复杂度是 O(1)，即常数空间复杂度。这是因为除了输入链表之外，我们没有使用任何与输入大小相关的额外空间。

总结

• 时间复杂度：O(m + n)
• 空间复杂度：O(1)

这个算法非常高效，因为它只需要线性时间，并且使用的额外空间是固定的。

2.去重

如果用unordered_set头文件的话，就非常简单。

// 删除链表中的重复元素
ListNode* removeDuplicates(ListNode* head) {
    if (!head) return nullptr;

    unordered_set<char> seen; // 用于存储已经出现过的元素
    ListNode* current = head;
    ListNode* prev = nullptr;

    while (current) {
        if (seen.find(current->value) != seen.end()) {
            //如果 current->value 存在于 seen 中，find 方法会返回一个迭代器，该迭代器指向集合中找到的元素。
            //如果 current->value 不在 seen 中，find 方法会返回 seen.end()，这是一个特殊的迭代器，表示集合的末尾。
            // 当前节点的值已经在 set 中，删除当前节点
            prev->next = current->next;
            delete current;
            current = prev->next;
        }
        else {
            // 当前节点的值不在 set 中，添加到 set 并继续
            seen.insert(current->value);
            prev = current;
            current = current->next;
        }
    }

    return head;
}

时间复杂度

1. 遍历链表：函数中有一个 while (current) 循环，它会遍历整个链表一次。每次迭代中，都会执行以下操作：

   • 检查当前节点的值是否在 seen 集合中（seen.find(current->value) != seen.end()）。
   • 如果当前节点的值已经存在于 seen 中，则删除当前节点，并更新指针。
   • 如果当前节点的值不在 seen 中，则将当前节点的值插入到 seen 中，并继续前进。

2. 查找和插入操作：对于 std::unordered_set，平均情况下，find 和 insert 操作的时间复杂度都是 O(1)。最坏情况下（当哈希冲突很多时），这些操作可能退化为 O(n)，但这种情况在实际应用中非常罕见。

因此，整个函数的时间复杂度是 O(n)，其中 n 是链表的长度。这是因为我们对链表中的每个节点都只进行了一次 find 和 insert 操作。

空间复杂度

1. 额外存储：seen 是一个 std::unordered_set，它用来存储链表中出现过的所有唯一值。在最坏的情况下，链表中的所有元素都是唯一的，那么 seen 将存储 n 个元素，其中 n 是链表的长度。

2. 其他变量：除了 seen 之外，我们还使用了一些指针变量（如 current 和 prev），它们占用的空间是常数级别的。

因此，该函数的空间复杂度是 O(n)，因为 seen 可能需要存储最多 n 个不同的元素。

总结

• 时间复杂度：O(n)
• 空间复杂度：O(n)

这个算法在时间和空间上都是高效的，因为它只需要线性时间来处理链表，并且使用的额外空间与链表中不同元素的数量成正比。如果链表中的元素数量很大且有很多重复元素，这个方法是非常合适的。

3.反转链表区间

// 反转链表区间
ListNode* reverseKGroup(ListNode* head, int k) {
    if (!head || k <= 1) return head;

    // 哑节点用于简化边界条件
    ListNode dummy(0);
    dummy.next = head;
    ListNode* prev = &dummy;
    ListNode* end = head;

    while (true) {
        // 查找当前区间的结束节点
        for (int i = 0; i < k && end; ++i) {
            end = end->next;
        }

        // 如果当前区间不足 k 个节点，则直接返回
        if (!end) break;

        // 断开当前区间与后续节点的连接
        ListNode* start = prev->next;
        ListNode* nextPrev = start;
        ListNode* current = start->next;
        start->next = end;

        // 反转当前区间
        while (current != end) {
            ListNode* next = current->next;
            current->next = start;
            start = current;
            current = next;
        }

        // 连接前一个区间和反转后的区间
        prev->next = start;
        prev = nextPrev;

        // 移动到下一个区间
        end = prev->next;
    }

    return dummy.next;
}

时间复杂度

1. 查找区间的结束节点：在 while (true) 循环中，我们首先使用一个 for 循环来查找当前区间的结束节点 end。这个 for 循环最多会执行 k 次。
2. 反转区间：如果找到了完整的 k 个节点，我们会进行反转操作。反转操作也是一个 while 循环，它会遍历这 k 个节点并重新链接它们。这个 while 循环也最多执行 k 次。
3. 连接前一个区间和反转后的区间：每次反转完一个区间后，我们需要更新指针以连接前一个区间和反转后的区间。这部分操作是常数时间 O(1)。

假设链表的长度为 n，那么整个链表会被分成若干个长度为 k 的子链表（最后一个子链表可能不足 k 个节点）。对于每个长度为 k 的子链表，我们都需要进行一次查找和一次反转，因此总的时间复杂度为 O(n)。具体来说，每次查找和反转都执行了 O(k) 的操作，而这样的操作总共需要进行 O(n/k) 次。

综上所述，该函数的时间复杂度是 O(n)。

空间复杂度

1. 哑节点：我们创建了一个哑节点 dummy 用于简化边界条件。这个哑节点只占用常数级别的额外空间。
2. 指针变量：我们使用了一些额外的指针变量（如 prev, start, nextPrev, current 等），这些变量也只占用常数级别的额外空间。
3. 不创建新的节点：在这个函数中，我们并没有创建任何新的节点，只是重新排列了现有的节点。

因此，该函数的空间复杂度是 O(1)，即常数空间复杂度。这是因为除了输入链表之外，我们没有使用任何与输入大小相关的额外空间。

总结

• 时间复杂度：O(n)
• 空间复杂度：O(1)

这个算法非常高效，因为它只需要线性时间，并且使用的额外空间是固定的。这种方法非常适合处理大型链表，因为它的内存占用非常低。

结

比较简单。