一、距离度量
1.欧氏距离
两个点在空间中的距离一般都是指欧氏距离
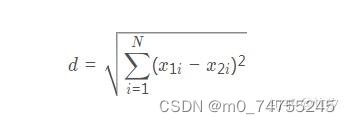
2.曼哈顿距离
也称为“城市街区距离”(City Block distance),曼哈顿城市特点:横平竖直


3.切比雪夫距离 Chebyshev Distance
国际象棋中,国王可以直行、横行、斜行,所以国王走一步可以移动到相邻8个方格中的任意一个
国王从格子(x1,y1)走到格子(x2,y2)最少需要多少步?这个距离就叫切比雪夫距离。
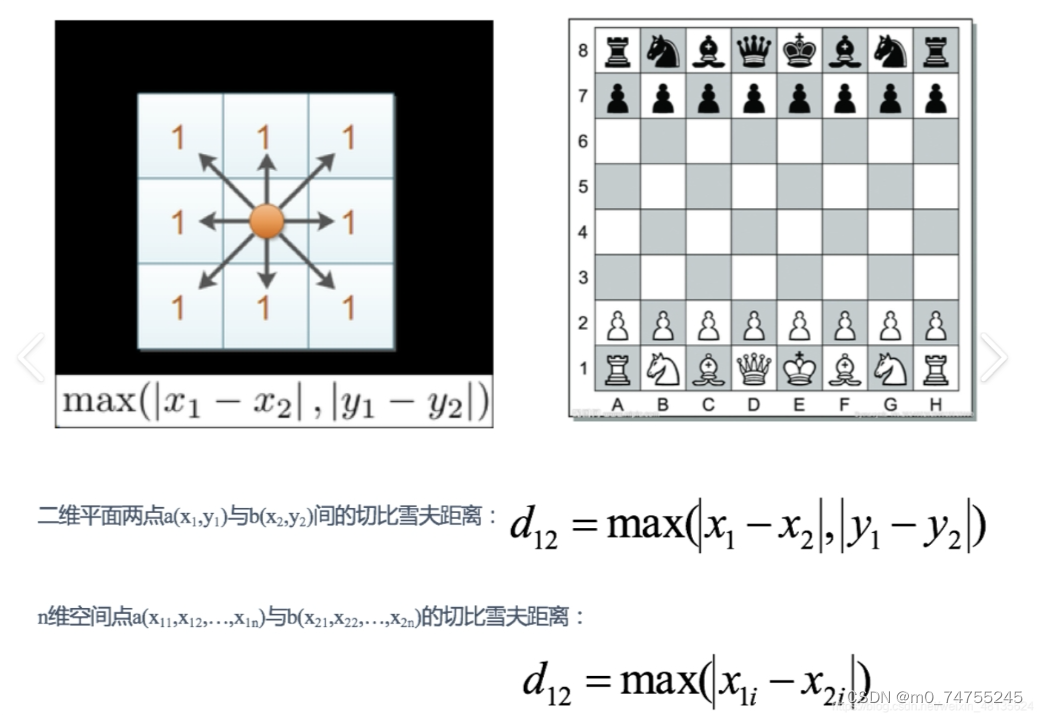
4.闵可夫斯基距离 Minkowski Distance 闵氏距离
•
不是一种新的距离的度量方式。
•
是对多个距离度量公式的概括性的表述

其中p是一个变参数:
当 p=1 时,就是曼哈顿距离;
当 p=2 时,就是欧氏距离;
当 p→∞ 时,就是切比雪夫距离
根据 p 的不同
,闵氏距离可表示某一类种的距离
二、特征预处理
1.进行归一化和标准化的原因
特征的单位或者大小相差较大,或者某特征的方差相比其他的特征要大出几个数量级,容易影响
(支配)目标结果,使得一些模型(算法)无法学习到其它的特征。
2.归一化和标准化
归一化
• 数据归一化:通过对原始数据进行变换把数据映射到【mi,mx】(默认为[0,1])之间
计算公式:

◆ 如果出现异常点,影响了最大值和最小值,那么结果显然会发生改变
◆ 应用场景:最大值与最小值非常容易受异常
标准化
•
数据标准化:通过对原始数据进行标准化,转换为均值为0标准差为1的标准正态分布的数据
计算公式:

◆ 如果出现异常点,由于具有一定数据量,少量的异常点对于平均值的影响并不大
◆ 应用场景:适合现代嘈杂大数据场景。
简单代码实例
import numpy as np
from sklearn.preprocessing import MinMaxScaler
from sklearn.preprocessing import StandardScaler
def dm01_MinMaxScaler(): #对特征值进行归一化
# 1. 准备数据
data = [[90, 2, 10, 40],
[60, 4, 15, 45],
[75, 3, 13, 46]]
# 2. 初始化归一化对象
transformer = MinMaxScaler()
# 3. 对原始特征进行变换
data = transformer.fit_transform(data)
# 4. 打印归一化后的结果
print(data)
def dm03_StandardScaler(): #对特征值进行标准化
# 1. 准备数据
data = [[90, 2, 10, 40],
[60, 4, 15, 45],
[75, 3, 13, 46]]
# 2. 初始化标准化对象
transformer = StandardScaler()
# 3. 对原始特征进行变换
data = transformer.fit_transform(data)
# 4. 打印归一化后的结果
print(data)
# 5 打印每1列数据的均值、方差和标准差
print('transformer.mean_-->', transformer.mean_) #均值
print('transformer.var_-->', transformer.var_) #方差
print('transformer.std_-->',np.sqrt(transformer.var_)) #标准差
dm01_MinMaxScaler()
dm03_StandardScaler()输出结果
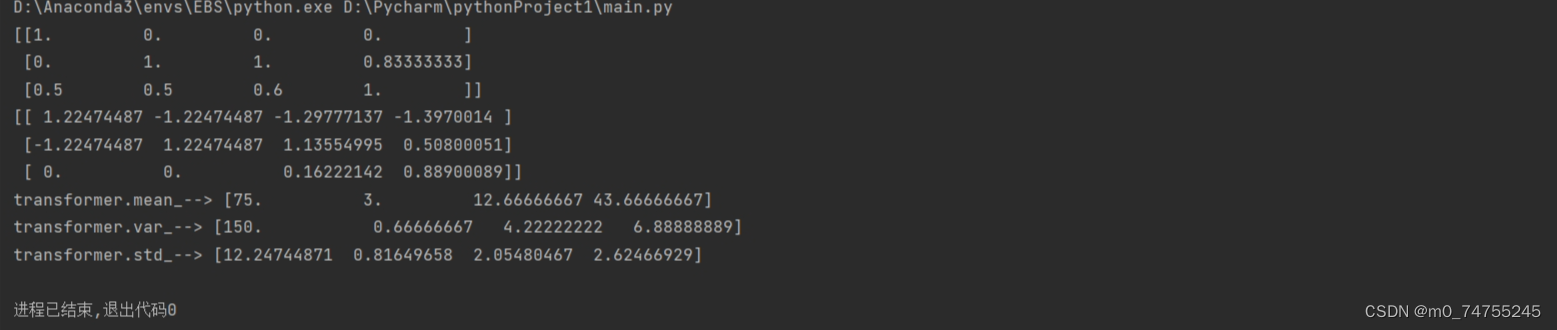
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








