目录
邻接矩阵,矩阵的计算及含义,完全图,补图,平面图的相关概念,欧拉图,最小生成树,最优二叉树
概述考点:
邻接矩阵,矩阵的计算及含义,完全图,补图,平面图的相关概念,欧拉图,最小生成树,最优二叉树
一.图



二.路和回路
2.1
②若路中的所有边互不相同,则称为迹;
若回路中的所有边互不相同,则称此回路为闭迹。
③若路中的所有结点互不相同,则称此路为通路;
若回路中除v0=vk外的所有结点互不相同,则称此回路为圈 。
2.2连通与可达
1.可达
在图G = <V, E>中,vi, vj∈V。
①如果从vi到vj存在路,则称vi到vj是可达的,否则称vi到vj不可达。规定:任何结点到自己都是可达的。
②如果vi到vj可达,则称从vi到vj长度最短的路的长度为从vi到vj的距离,记为d(vi, vj)。如果vi到vj不可达,则通常记为d(vi, vj) = ∞。
2.连通
无向图:
①若无向图G中的任何两个结点都是可达的,则称G是连通图,否则称G是非连通图。
通俗的讲:图G的一个连通分支是图G的一个极大连通子图,一个图被分成几个小块,每个小块是连通的,但小块之间不连通,那么每个小块称为连通分支。一个孤立点也是一个连通分支
连通分支数用W(G)表示。
②设无向图G=<V,E>为连通的,若有结点集V1⊆ V,使得图G删除了V1所有结点后,所得的子图是不连通的,而删除了V1的任意真子集后,所得的子图仍然是连通图。则称集合V1为图G 的点割集。若某一结点就构成点割集,则称该结点为割点。
点割集: 个人理解:删掉一堆点不连通,删掉一堆点里的一个或者任意几个还是连通的
边割集:同上述
④若G不是完全图,定义G的点连通度(或连通度)为:
k(G)=min{|V1| V1是G的点割集} 。
注:一个不连通图的点连通度等于0,
存在割点的连通图的点连通度为1。
类似地,定义非平凡图G的边连通度为:
λ(G)=min{|E1|E1是G的边割集}
有向图:
设G = <V, E>是一个有向图,
①略去G中所有有向边的方向得无向图G’,如果无向图G’是连通图,则称有向图G是连通图或称为弱连通图。否则称G是非连通图;
②若G中任何一对结点之间至少有一个结点到另一个结点是可达的,则称G是单向连通图;
③若G中任何一对结点之间都是相互可达的,则称G是强连通图。
有向图G是强连通图的充分必要条件是G中存在一条经过所有结点的回路。
三.图的矩阵表示
3.1邻接矩阵


3.2可达性矩阵
按照线性代数中的算法算,结果中的大于1 的数字都换成1 所形成的
3.3无向图的完全关联矩阵
(1)给定无向图G,令v1,v2,…,vp和e1,e2,…,eq分别记为G的结点和边,则矩阵M(G)=(mij),其中
1关联,0不关联
3.4有向图的完全关联矩阵

四.特殊的图
4.1欧拉图和哈密尔顿图
设G是无孤立结点的图,若存在一条路(回路),经过图中每边一次且仅一次,则称此路(回路)为该图的一条欧拉路(回路)。
具有欧拉回路的图称为欧拉图。
规定:平凡图为欧拉图。
以上定义既适合无向图,又适合有向图。
总结:
(1)仅有欧拉路而无欧拉回路的图不是欧拉图;
(2)图中是否存在欧拉路、欧拉回路的判定非常简单,只需要数一下图中结点的度数即可;
定理 无向图G = <V, E>具有一条欧拉路,当且仅当G是连通的,且仅有零个或两个奇度数结点。
(3)使用Fleury算法求欧拉路(回路)时,每次走一条边,在可能的情况下,不走桥。
哈密尔顿图:
经过图中每个结点一次且仅一次的路(回路)称为汉密尔顿路(回路)。
存在汉密尔顿回路的图称为汉密尔顿图。
规定:平凡图为汉密尔顿图。
以上定义既适合无向图,又适合有向图。
五.平面图
如果能把一个无向图G的所有结点和边画在平面上,使得任何两边除公共结点外没有其他交叉点,则称G为平面图,否则称G为非平面图。
当且仅当一个图的每个连通分支都是平面图时,这个图是平面图。

平面图中所有面的次数之和等于边数的二倍。
六.对偶图
对于具有n个面的平面图G=<V,E>,实施下列步骤所得到的图G*=<V*,E*>,称为G的对偶图:
(1)在G的每一个面 ri内部作一个G*的顶点vi*∈V*;
(2)若G的面ri与rj有公共边界ek,那么过边界ek,作关联vi与vj的一条边,且与其他边不相交;
(3)当且仅当ek为ri一个面的边界而非与其他面的公共边界时,作vi*的一条环与ek相交,且仅交于一处,并不与G*的边相交。
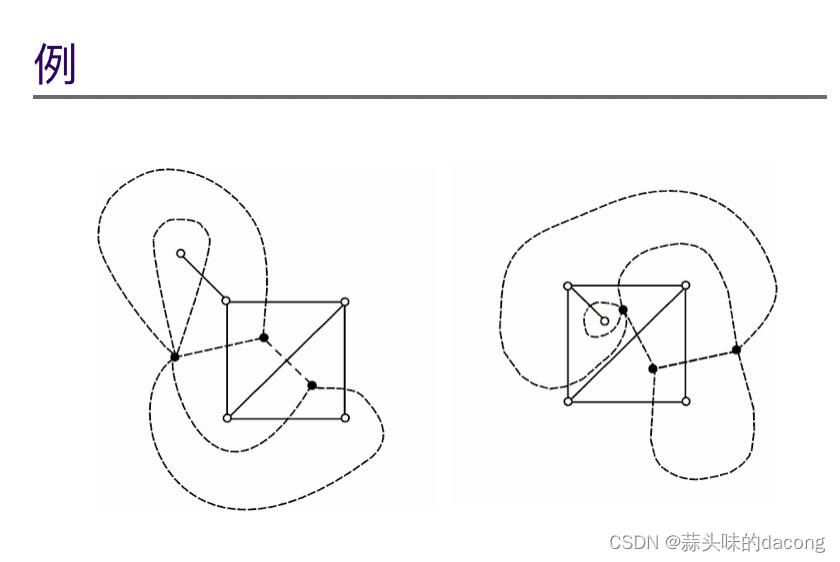
G 的对偶图G*有以下性质:
(1) G*是平面图
(2) 若边e为G中的环,则G*与e对应的边e*为桥,若e为桥,则G*中与e对应的边e*为环.
(3) 同构的平面图的对偶图不一定是同构的.
如上面的例子.
七.树与生成树
7.1
1. 连通而不含回路的无向图称为无向树,简称树,常用T表示树。
2.树中度数为1的结点称为树叶;度数大于1的结点称为分支点或内部结点。
3.每个连通分支都是树的无向图称为森林。
4.平凡图称为平凡树。
5.树中没有环和平行边,因此一定是简单图
6.在任何非平凡树中,都无度数为0的结点。
具体总结方法:
连通-->不含回路-->树
不连通-->不含回路-->森林
生成树:
(1)定义
给定图G = <V, E>,若G的某个生成子图是树,则称之为G的生成树,记为TG。
生成树TG中的边称为树枝;G中不在TG中的边称为弦;TG的所有弦的集合称为生成树的补。
定义 设G = <V, E>是连通的带权图,T是G的一棵生成树,T的每个树枝所赋权值之和称为T的权,记为W(T)。G中具有最小权的生成树称为G的最小生成树。 
7.2 有序树与二叉树之间的转换
(1)任何一棵有序树都可以改写为一棵对应的二叉树。方法如下:
加线:在兄弟结点之间加一连线;
抹线:对任何结点,除了其最左的孩子
外,抹掉该结点原先与其孩子之
间的连线;
旋转:将水平的连线和原有的连线,以
树根结点为轴心,按顺时针方向
粗略地旋转450。
7.3最优树与哈夫曼算法
设有一棵二叉树,若对其所有的t片叶赋以权值w1、w2、…、wt,则称之为带权二叉树;若权为wi的叶的层数为L(wi),则称 为该带权二叉树的权;而在所有带权w1、w2、…、wt的二叉树中,W(T)最小的二叉树称为最优二叉树。
哈夫曼算法
1952年,D.A.Huffman给出求最优二叉树的算法。
首先找出两个最小权值,设为w1和w2,然后对t-1个权w1+w2,w3,…,wt求作一棵最优树,并且将这棵最优树的结点w1+w2分叉生成两个儿子w1和w2,依此类推。

7.4编码问题
前缀码

(2)用二叉树产生前缀码
给定一棵二叉树T,假设它有t片树叶。
设v是T任意一个分支点,则v至少有一个儿子至多有两个儿子。若v有两个儿子,则在由v引出的两条边上,左边的标上0,右边的标上1;若v只有一个儿子,在v引出的边上可标0也可标1。设vi为T的任意一片树叶,从树根到vi的通路上各边的标号组成的符号串放在vi处,t片树叶处的t个符号串组成的集合为一个前缀码。
左零右一






















 8718
8718











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








